课程内容
C语言的数学运算
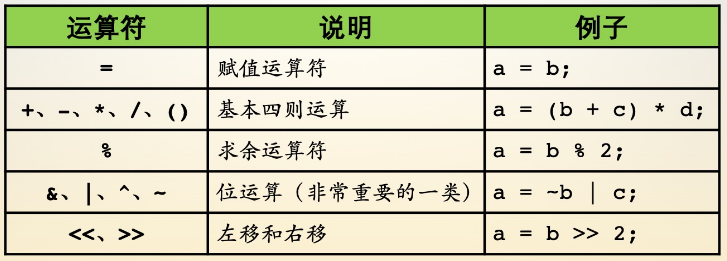
-
-
= 赋值
- 可以与和其他运算符结合使用:+=、<<=、...
-
/ 除以
- 左右都是整数:整除,下取整
- 左右至少有一个浮点数:得到的才是浮点数
-
() 提高运算优先级
-
⭐位运算,效率高
- 计算机对于不同的数据类型,都统一按二进制数据存储,即按bit位存储
- 8bit→1byte
- int类型是32位bit,对于有符号的最大能表示2^31-1
- 位运算时,①先展开成二进制位表示,②只有对应的位之间有关系
- 位运算不支持浮点数?
- 没有意义。对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。
- 如果按位与,前面12位运算规则是什么呢?即指数位相与结果的意义是什么呢?这就是本质了,两个浮点数相与没有数学意义啊。
- ^ 异或
- 特点:是自己的逆运算;支持交换律、结合律
- 逆运算
- 前提:符合交换律
- 减法、除法不符合
- 减法是加法的逆运算,反之不是
- 除法是乘法的逆运算,反之不是 [非严格,未考虑乘数为0]
- 前提:符合交换律
-
<< 左移 >> 右移
- 左移一位,乘以2
- 右移一位,除以2,下取整,符号不变
- 左边一直补符号位(最高位为符号位的有符号数)
- 左边强制补0(无符号数)
C语言的数学函数
头文件:math.h
注:abs()函数在stdlib.h里
| 原型 | double pow(double a, double b); | 指数函数 |
|---|---|---|
| - | double sqrt(double x); | 开平方 |
| - | double ceil(double x); | 上取整 |
| - | 返回的还是double,因为double能够表示超出int的范围的数 | |
| - | double floor(double x); | 下取整 |
| - | int abs(int x); | 整数绝对值;stdlib.h |
| - | doublefabs(double x); | 实数绝对值;f也许在以前代表float |
| - | double log(double x); | 以e为底的对数 |
| - | double log10(double x); | 以10为底 |
| - | 换底公式可以求以任何数为底的对数:log(2)8 = log(8) / log(2) | |
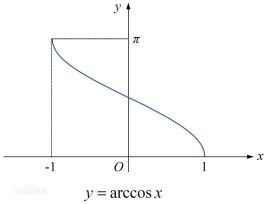
| - | double acos(double x); | 反余弦函数:arccos() |
| 返回值:角度的弧度值 ⭐π = acos(-1) |
随堂练习
-

- double类型的控制字符是“%lf”
- scanf的控制字符必须与参数的类型对应,否则读不进
-
double x;
-
scanf时一定要用“%lf”对应,不能用“%f”,否则如下:
-

- printf没有它严格,控制字符可以不和类型完全一样,应该是有类型转换
- 代码
-
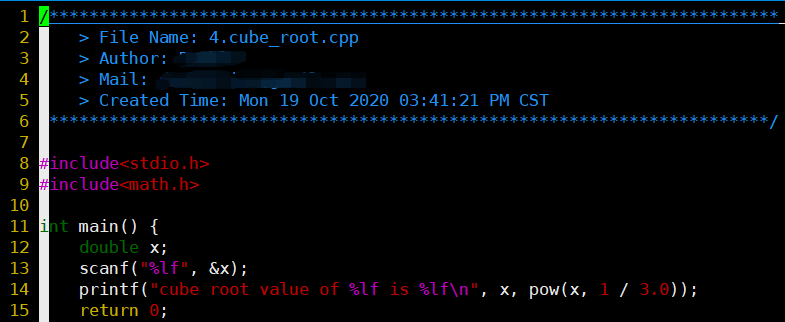
- 巧妙地是用pow,三分之一次方表示立方根
- ⭐1/ 3**.0**而不可以是 1 / 3
- gcc编译时要添加math库,加-lm
-
-
-
-

- 注意π可以用acos(-1)得到更精确的表示
- 代码
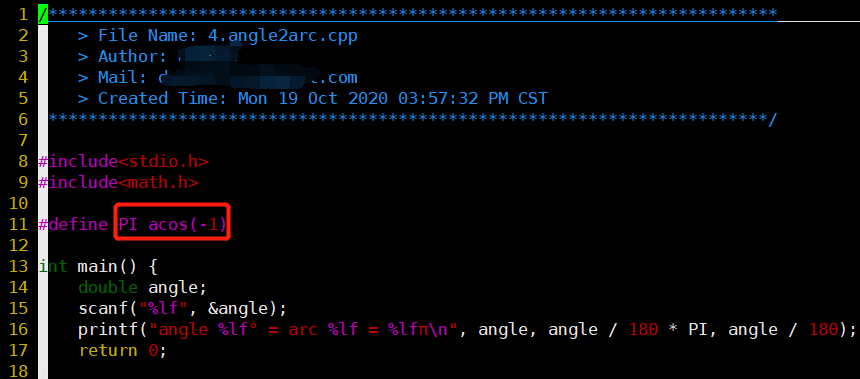
- 先除后乘更安全,不容易溢出
亮点笔记
- double类型的控制字符是“%lf”
- π可以用acos(-1)得到更精确的表示
代码演示
练习
-
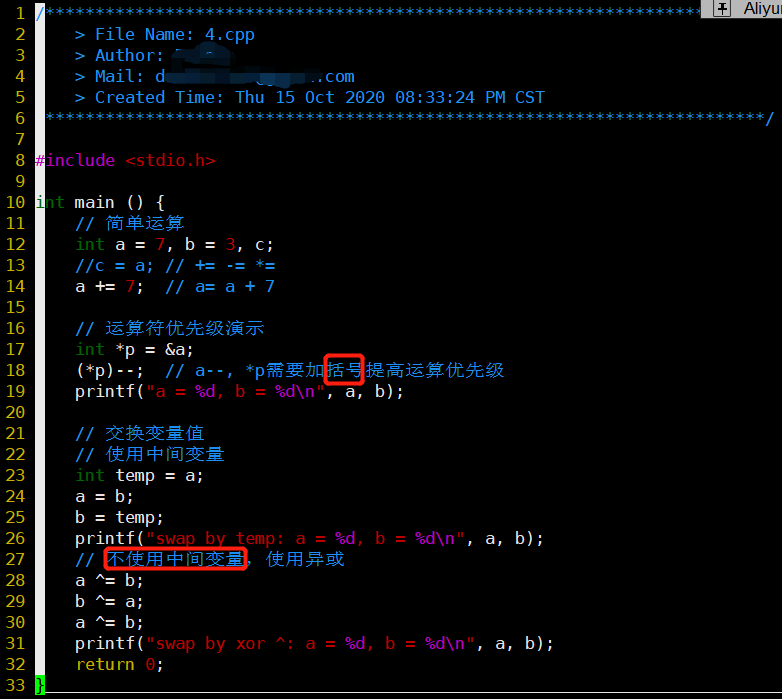
-
用异或做交换思路清奇,但其实并不推荐
- 只能用于整型,才能异或
- 速度并不比使用temp快
- 同一个变量之间swap就会变成0:swap(a, a)
附加知识点
- 运算符优先级+结合顺序表-百度
- p--的运算顺序是 ①p指向的地址-1,②再用取该地址的值
- (*p)--才是①先取p指向地址的变量值,再将变量的值-1
- p--的运算顺序是 ①p指向的地址-1,②再用取该地址的值
- 异或规律
- a ^ a = 0;
- 0 ^ a = a;
- 可以在一个数字均出现两次的数组中找有且一个只出现一次的数字
- xshell运行C语言不报warning
- g++ *.cpp -Wall
- 使用该选项,允许发出GCC能够提供的所有有用的警告
- 也可以用-W{warning}来标记指定的警告。
-
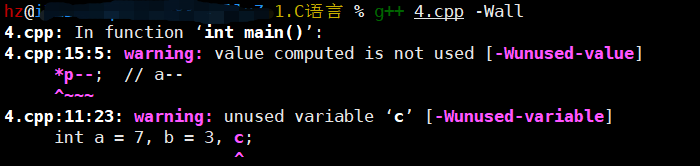
- g++ *.cpp -Wall
思考点
- 用异或运算进行变量交换有什么好处?
-
节约第三方变量的内存
-
原理思考
- 逆运算即可
-
或者
-
自身与自身异或为0
* 任何变量和0异或值不变 -
按上面的原理思考,其实也可以用+-运算来做?
- a' = a + b
- b = a' - b = a
- a = a' - b = a' - a = b
- 但是这样做并没有用到位运算的高效性,而且要保证两个数的和不溢出~
-
Tips
-
C语言文档中文版-极客学院翻译
- C语言大约有29个函数库
-
参考工具书章节
-




