课程内容
函数基础知识
- 函数封装
- 可读性、美观性、⭐调试性(按函数模块debug即可)
- 函数声明三组成(必须)
- 返回值
- 无返回值写void
- 函数名
- 参数声明列表
- 参数类型+参数名
- 返回值
- 函数定义
- 花括号里的内容
递归函数
- 一类编程技巧(for循环、if语句、递归),而不是算法(递推)
- 函数自己调用自己
- 组成部分
- 语义信息:根据需求设计
- 边界条件:设计递归出口,可以有多个
- 递推公式:针对问题!
- 结果返回:不只是通过return
- 两种方式:return返回、传出参数(指针)
- 怎么证明递归函数是正确的?
- 简单递归:将中间过程展开
- 向下递推+向上回溯
- 复杂递归:数学归纳法
- 比如阶乘
- fac(1)成立
- 假设fac(k)正确
- 证明fac(k+1)正确,即可
- 比如阶乘
- 简单递归:将中间过程展开
函数指针与应用
-

-
将函数名以指针的形式传入函数,在函数中通过函数名可以直接使用函数
- 返回值 (*函数名)(参数类型列表)
-
应用
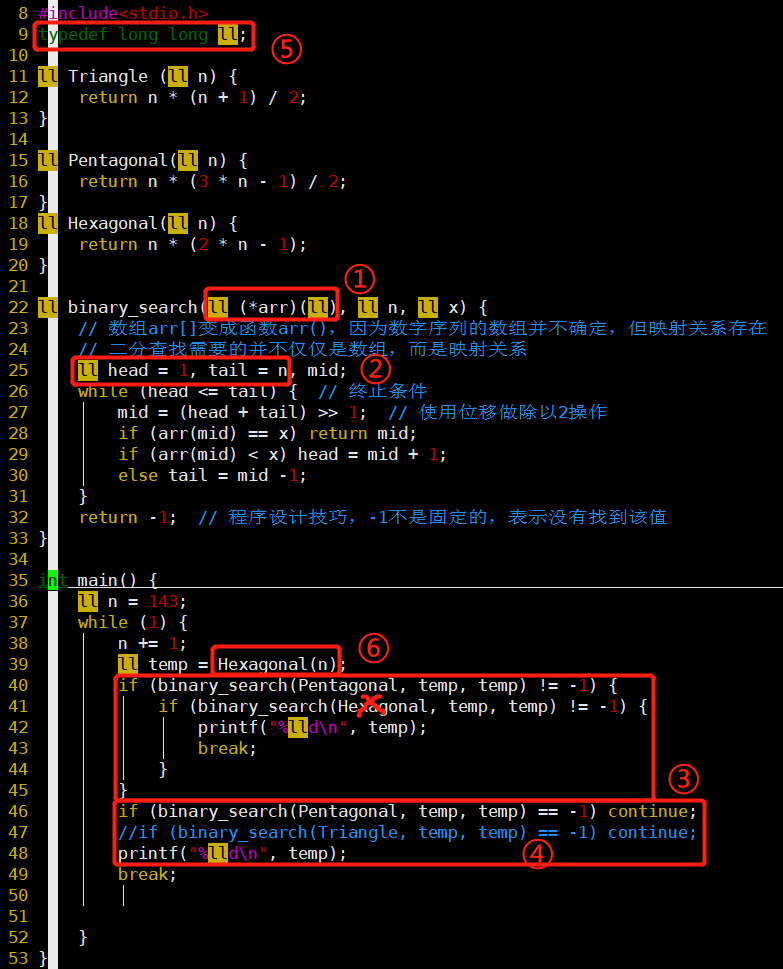
⭐EP-45亮点很多,主要注意6个关键
- 二分查找的不一定是数组,有映射关系的单调序列即可
2. 根据序列特点调整了区间头、尾 - 对偶逻辑减少缩进,增加可读性
- 三角形数包含六边形数:第2n-1个三角形数=第n个六边形数
- 如果用int类型(4字节),会陷入死循环
- int类型不足以涵盖下一个所求数字
- 用long long int类型(8字节),控制字符:%lld
- 固定六边形数,跨度更大,速度更快,且根据第4点可知其一定是三角形数
- 其他
- 应该可以用比temp更小的右边界或比1更大的左边界
- 不过因为是O(logn),所以缩小后效果提升不会很大
- 这里用了函数指针,如果不用,得写多少个差不多的binary_search函数?
- 不过也可以用宏去做函数的切换
- 图中红叉处为笔误,Hexagonal修改为Triangle
- 应该可以用比temp更小的右边界或比1更大的左边界
欧几里得算法
又叫辗转相除法
- 快速计算最大公约数
- 如果gcd(a, b) = gcd(b, a % b) = c,将使规模变小
- 证明
①设c为a、b的最大公约数,证明b、a % b也存在公约数c
设正整数k1、k2、k3
a = k1 * c
b = k2 * c
a % b = a - k3 * b // 取模的本质
所以a % b= k1 * c - k3 * k2 * c =(k1 - k3 * k2) * c
即a % b是c的倍数,又b是c的倍数
故c是两者的公约数
②证明c是最大的公约数
证明b、a % b的另两个约数k2、k1 - k3 * k2互质即可
设gcd(k2, k1 - k3 * k2)= d (正整数),即证d = 1
设正整数m、n,可令
k2 = m * d
k1 - k3 * k2 = n * d
则
k1 =n * d + k3 * k2 =(n + k3 * m) * d
可得
gcd(k1, k2) >= d
又因为
gcd(a, b) = c
a = k1 * c
b = k2 * c
即
gcd(k1, k2) = 1
所以
d = 1
-
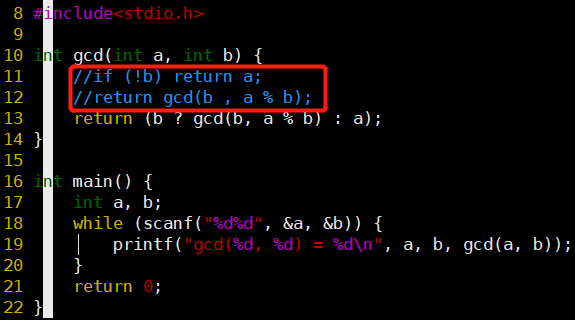
代码
-
-
递归函数
- 可用一句实现gcd函数
- 将if语句换成问号表达式
- 可用一句实现gcd函数
-
不需要根据a、b大小交换顺序?不需要
- 如果a ≥ b:gcd()函数按正常思维进行
- 如果a < b:gcd()函数将交换两个变量
-
Ctrl+D会重复上次输出而不是终止?
- 【返回读入的字符数为0时会终止,比如输入非一个int值】
- 因为没有对scanf返回值是EOF的判断
- 可以在scanf前取反"~" 或 在后面做-1判断
扩展欧几里得算法
- 快速求解ax+by=1的一组整数解
- gcd(a, b) = C的C为何值时,能求解一组整数解
- C可取1或>1两种情况
- gcd(a, b) = C的C为何值时,能求解一组整数解
a = nC
b = mC
nCx + mCy = 1
C(nx + my) = 1
nx + my必定≥1
C只能取1
- 在辗转相除法最后一轮只剩下1、0时,即互质时,就说明有整数解
- 数学归纳法
- 流程
-
对于f(0)成立→假设f(k)成立→若可以得到f(k+1)也成立→则k为任意都可以成立
-
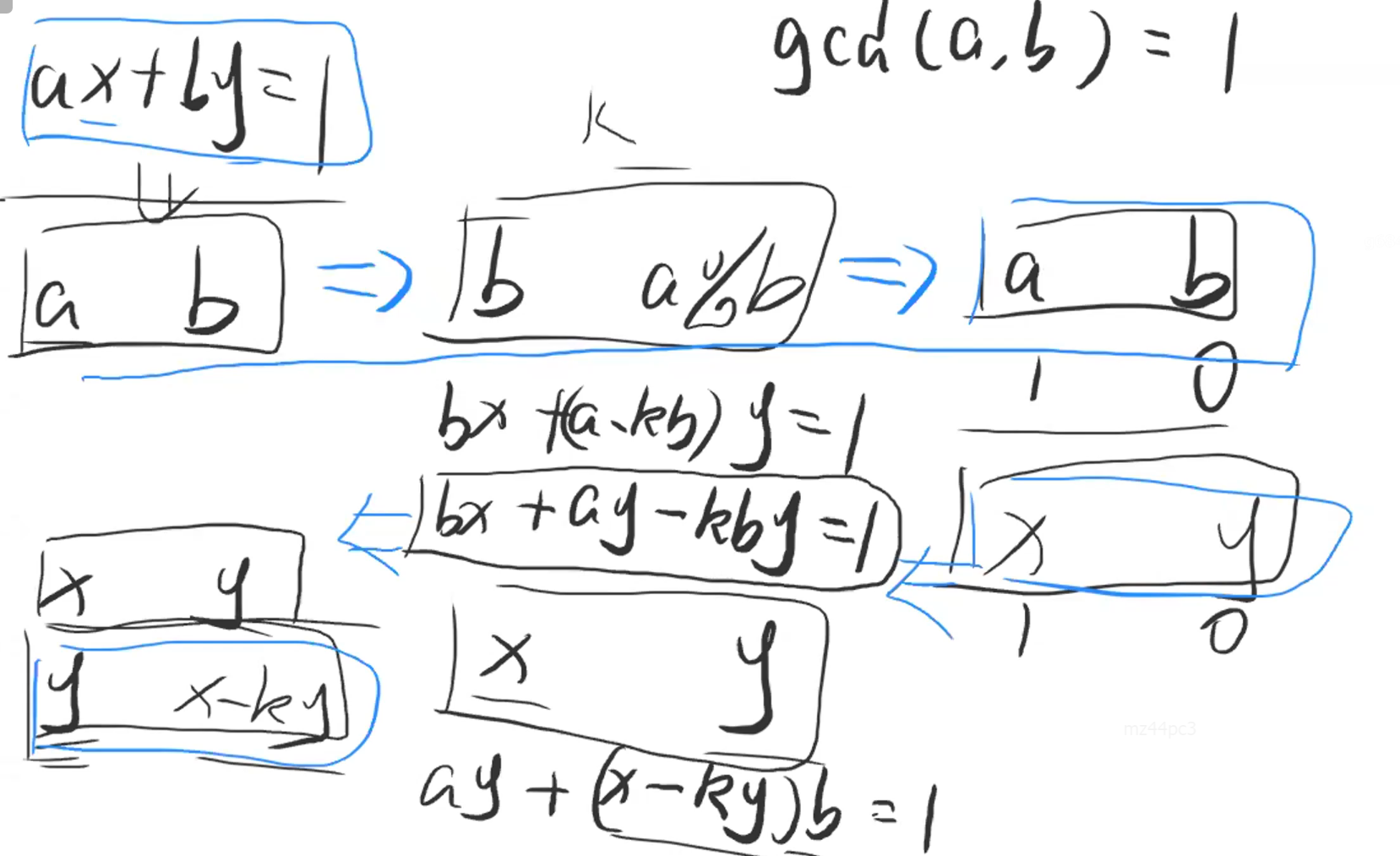
-
参考上图、下表,向下递推+向上回溯
-
- 流程
| a | b | x | y | |
|---|---|---|---|---|
| 第k+1层(推导) | a | b | y | x - ky |
| ↓↓↓ | ↓↓↓ | ↑↑↑ | ↑↑↑ | |
| 第k层(假设) | b | a % b | x | y |
| ... | ↓↓↓ | ↓↓↓ | ↑↑↑ | ↑↑↑ |
| 第0层(成立) | 1 | 0 | 1 | 0(任意) |
代码
-
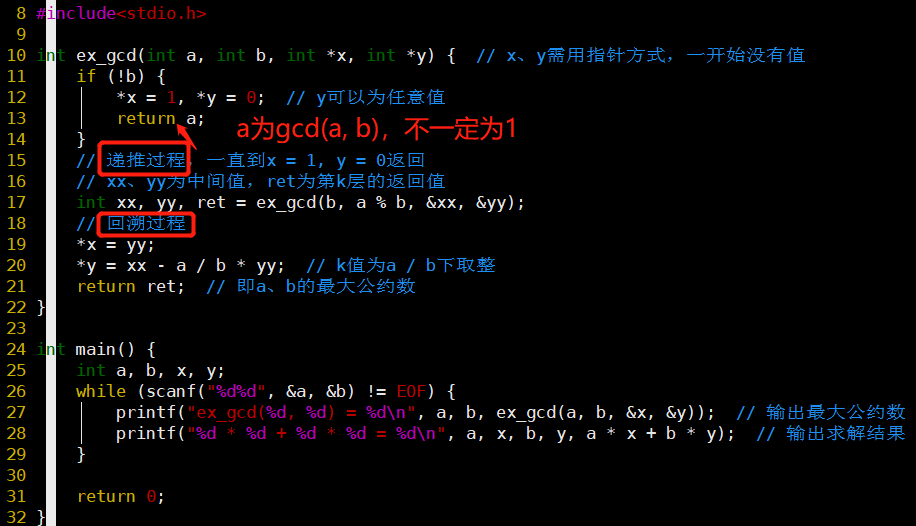
-
函数输入的地址一开始没有值,一直到最深处才赋值,再回溯
-
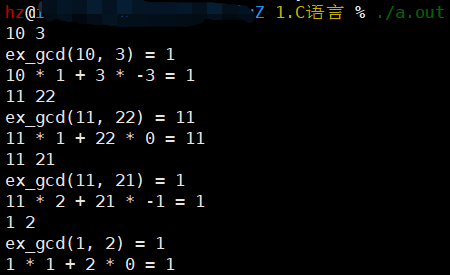
-
输出的等式右边不一定是1
- 其实扩展欧几里得算法可以快速求解ax + by = gcd(a, b)的整数解
变参函数
通过上述场景来学习:
- 问题不是函数如何声明,而是该如何定位到变参列表的每一个参数
- 不知道变参列表里变量的名字
- 举例:老师想找张三同学后面一位同学回答问题,但忘记名字了,可以直接叫张三同学后面一位来回答
- 通过va一族来实现 <stdarg.h>
- 变量:va_list类型,获取a往后的参数列表
va_list arg;
-
- 函数
-
-
- va_start:定位到变参列表第一参数的位置
-
va_start(arg, n); // n为变参列表的前一个变量
-
-
- va_arg:返回下一个类型匹配的表达式
-
va_arg(arg, int);
-
-
- va_end:结束对可变函数实参的遍历,清除va_list空间
-
va_end(arg);
-
代码
-
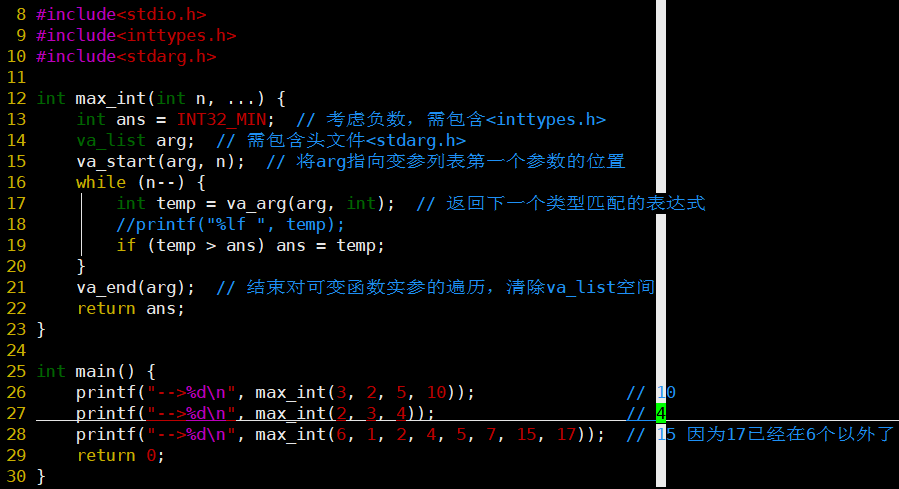
-
细节见注释,包含头文件、va_arg类型匹配、最多遍历次数、va_end清空、int最小值
-
当不确定某方法所在的头文件时,使用gcc编译可能会提示需要包含的头文件
-

不过在本机的Xshell上就算使用-Wall也没有显示,老师使用的是Mac
随堂练习
-

-
代码
-

没有考虑负数输入,但不是重点~
代码演示
简版printf函数的实现
- 实现打印字符的功能(从0到1的一步)
- putchar('x')函数:向标准输出输出一个字符'x'
- 输出字符串功能:"hello world",并有返回成功打印字符数的功能
-
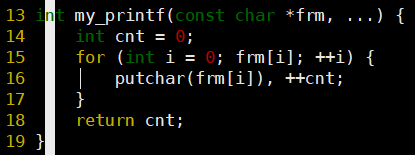
- 系统会自动给字符串末尾加'\0',其对应十进制值为0;eg. 'a'→97
- const修饰符是为了让传入的字符串字面量不被修改,也不能被修改
-
不加的话,在C中不会警告,但在C++中会报警告,如下:
-

-
另:char *const frm
- 不能修改frm指针(如char *p; frm = p;),但是可以修改该指针指向的内容
- 参考const char * 、char const *、 char *const三者的区别-CSDN,前两者相同
-
- 字符指针取字符串第i位的值可以用两种方式
- frm[i]
- *(frm + i)
- 让%d控制字符生效,输出整数
- 向屏幕输出'%'
-
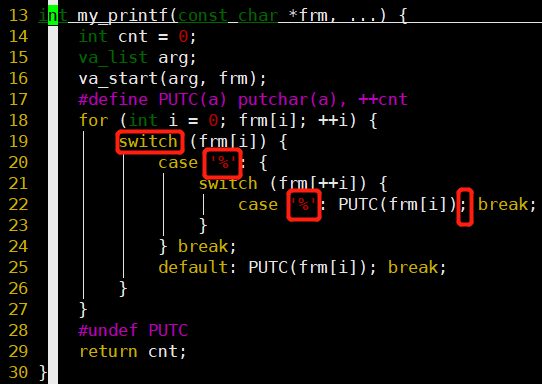
- 使用switch结构
- break前面不能是逗号,需要是分号
- 向屏幕输出正整数123
-
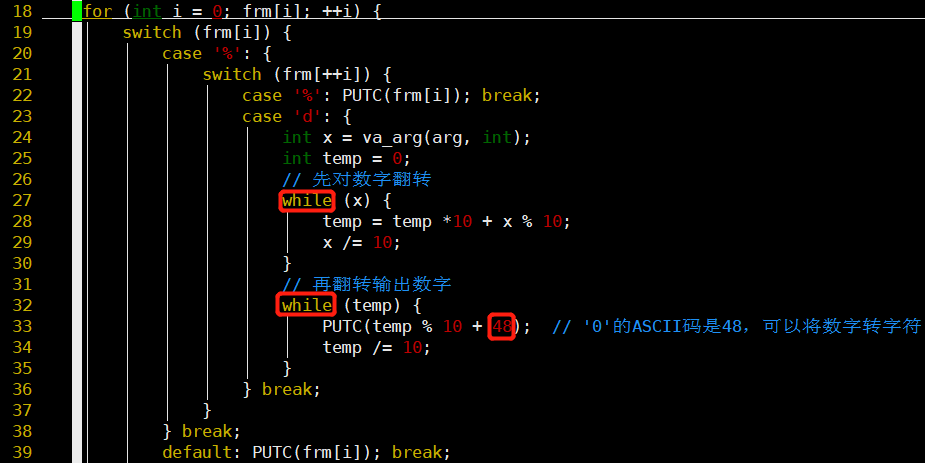
- 通过两个while循环,将数字翻转再翻转输出
- 不翻转的话,只能从低位开始遍历输出
- 数字+字符'0'(即48),可以将数字转为字符输出
- ❌无法输出整数0
- 向屏幕输出正整数0
- 通过两个while循环,将数字翻转再翻转输出
-
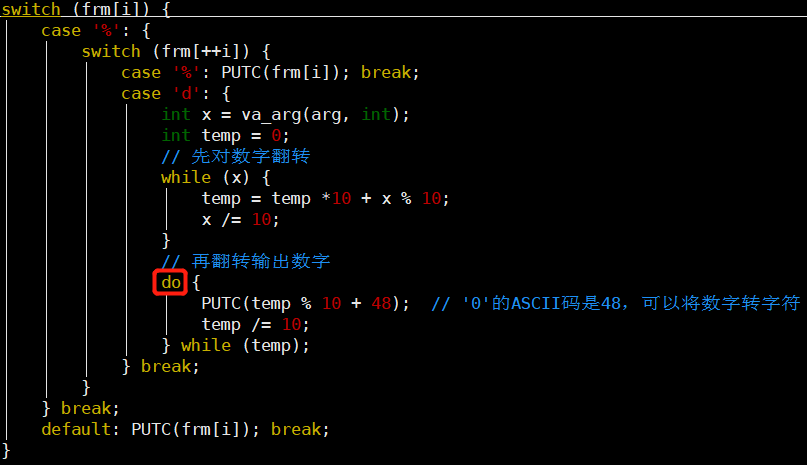
-
do...while与while的区别
-
❌对于正整数1000,输出为1
- 向屏幕输出正整数1000
-
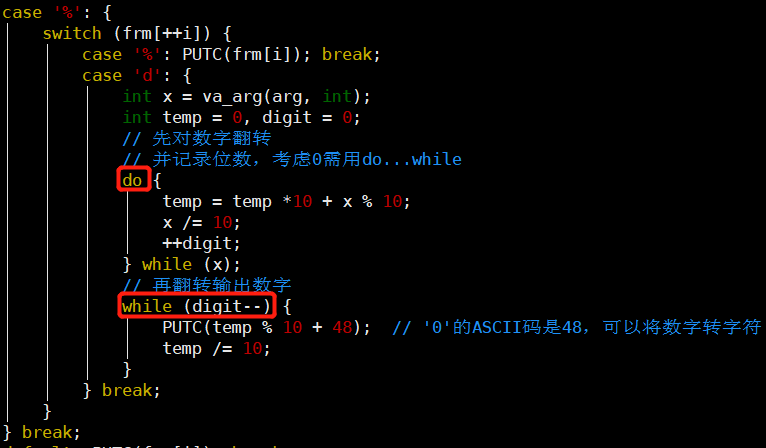
-
记录数字位数,考虑0值,换成do...while方式
-
第二次翻转可以使用do...while(--digit)
- 但为了避免digit为0时陷入死循环,使用while(digit--)先判断digit位数更保险
- 虽然digit为0几乎不可能出现
-
❌错误样例
-
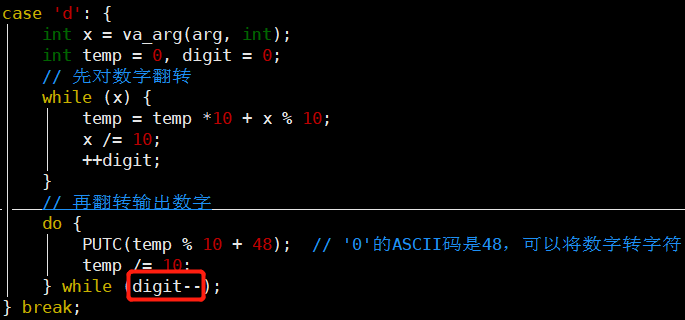
-
digit--时,输出数字1000时,会多一位
- --digit则可能陷入死循环,无限循环输出0
- 因为输入为0时,记录的数字位数为0(见下),--digit就变成了-1
- --digit则可能陷入死循环,无限循环输出0
-
第一个while循环计算0的位数时,为0,有误!
-
❌对于负整数,输出有误!
- 向屏幕输出负整数-123
-
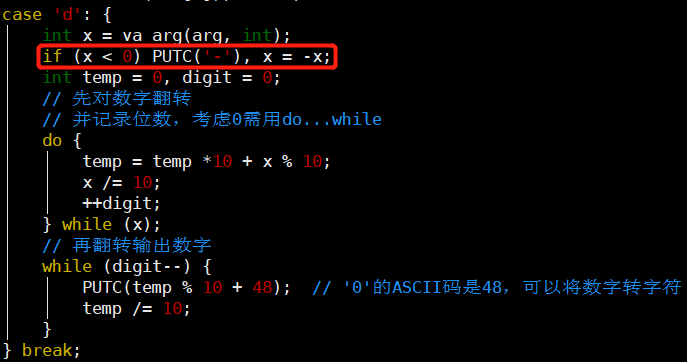
-
只需加个负数判断
-
❌对于INT32_MAX、INT32_MIN,输出有误!
- 向屏幕输出INT32_MAX(2^31 - 1)、INT32_MIN(-2^31)
-
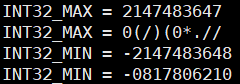
-
INT32_MAX翻转后,int类型表示不下→切块翻转
-
5位5位切成两部分→两部分分别翻转→两部分分别翻转输出
-
24174 / 83647 →47142 / 74638 →24174 83647
-
代码
-
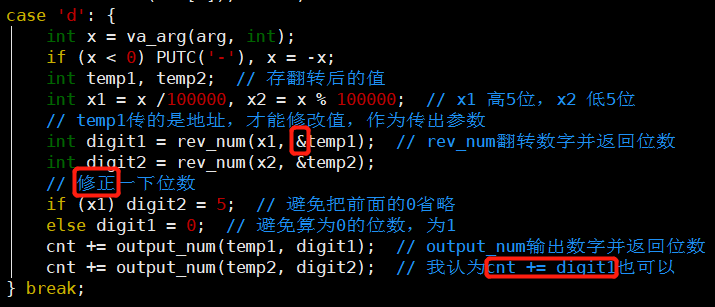
- rev_num传temp1地址才能使其值能被修改
- output_num所做的返回位数操作,我认为可以直接通过digit1、2得到
- 记得修正高5位、低5位的实际位数
- rev_num和output_num函数如下:
-
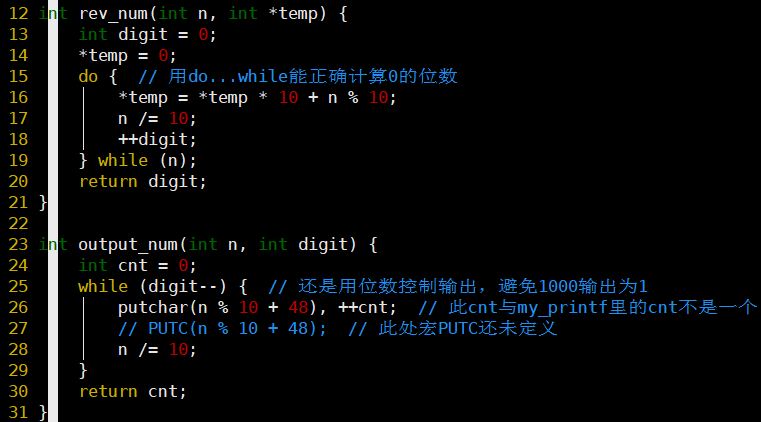 * output_num里PUTC并不生效,考虑编译时其顺序在PUTC定义前
* output_num里PUTC并不生效,考虑编译时其顺序在PUTC定义前
-
- ❌对于INT32_MIN,输出还有误!
-
-
-
此时INT32_MIN输出还是不对,因为
-
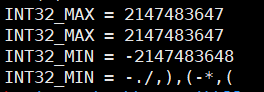
-
INT32_MIN取负数还是它本身,正数可表示不下了
-
负数绝对值比正数大一
-
INT32_MIN:1000...000
- →⭐求相反数:取反+1→0111...111 + 1
- →1000...000(本身)
-
代码
-
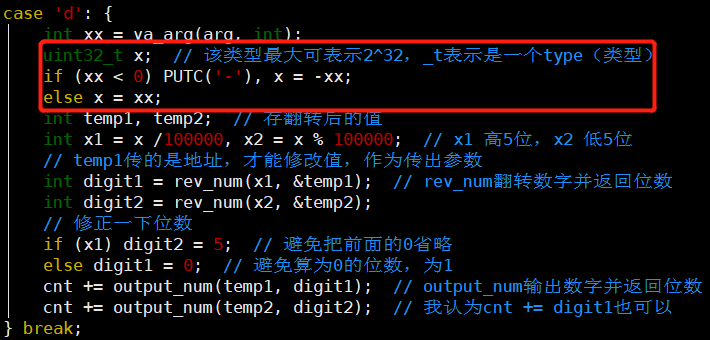
-
使用无符号整型uint32_t来存储即可!
-
-
- 让%s控制字符生效,输出字符串
- 很简单,加入一个case即可
-
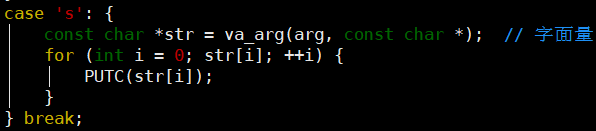
- 注意字面量要用const char *
-
- 检验返回值功能
附加知识点
-
K&R风格的函数定义
-

-
对参数列表里参数的声明放在了后面
-
上古级别的写法,了解即可,不推荐使用
-
-
使用%g控制字符可以以更友好的方式输出数字的有效位
-
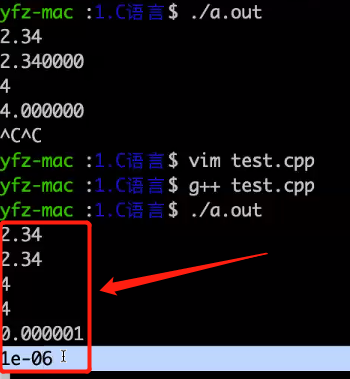
-
数组:展开的函数;函数:压缩的数组
-
int和long的区别-简书
- 不同位数系统下大小不同
- long -> 32位:4字节;64位:8字节
- 但int都是4字节,long long都是8字节
-
算法是什么?聪明人的做事方法
-
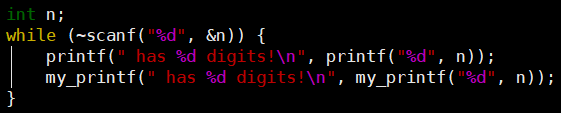
⭐while(~scanf("%d\n", &a))
- while(scanf("%d\n", &a) != EOF) 可以用while(~scanf("%d\n", &a))代替
- ~是位取反,EOF即-1,按位取反即为0
-
undef宏定义时只需加宏名,不需要加参数,如:
#define PUTC(a) putchar(a)
#undef PUTC
- ⭐二进制求相反数:取反+1
- 无论正负,是互逆的,两次该操作则回到本身
- 与-1再取反一样
思考点
-
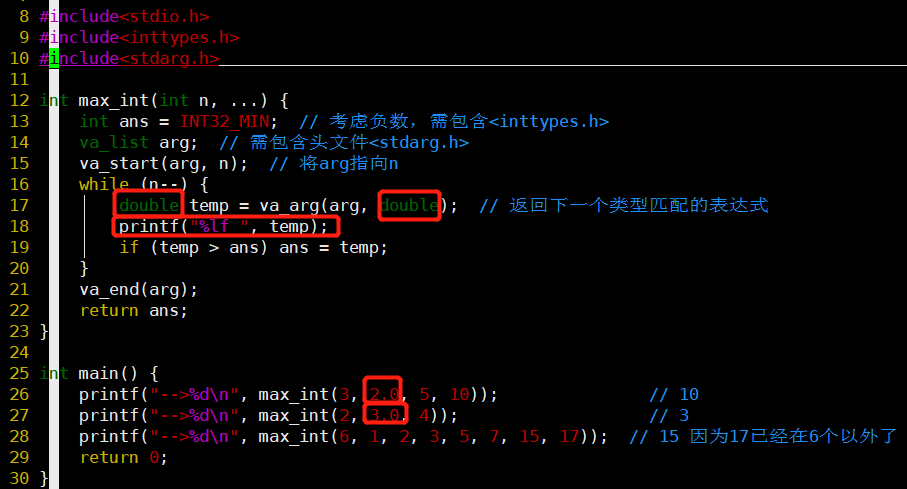
💡va_arg对于类型不匹配时是怎么处理的?
-
-

-
对于输出有两个问题:
- 第一行,第一个int值获取不到时,输出的是0.000000,第二次却是nan?
- 第三行,输入的全是int类型,但却获取到了第二个数字:3.000000,实验证明,这个数字和第二行的3.000000有关,是因为va_list没有清理干净吗?
-
❓对于什么类型就会往后走多少长度的地址去获取值
- 如double,就是往后获取8个字节对应的变量
-
💡但对于覆盖还是未清理的问题,不知道无法解释~
-
如果能打印va_list的地址就更好了~
-
Tips
- 刷刷OJ
- 参考工具书第7章