工程实现中应用非常广泛
课程内容
<5个平衡条件>
- 结点非黑即红
- 根结点是黑色 [头发]
- 叶结点 (NIL) 是黑色 [不洗脚]
- 通常不用画出来,也不用考虑NIL结点,默认是黑色
- 红色结点的两个子结点都是黑色⭐
- 红色结点不能接红色结点
- 从根结点到所有叶结点的路径上,黑色结点数量相同⭐
平衡条件的认识
- 4th+5th条件 👉 在红黑树中,最长边结点数量 : 最短边结点数量 = 2 : 1
- 本质上,红黑树也是靠树高控制平衡
- 红黑树比AVL树的树高控制条件更松散
- 所以在红黑树中插入或删除结点以后,发生调整的概率更小,降低了调整损耗
- Top-3条件基本是废话,想染什么颜色就染什么颜色,想变色就变色,NIL默认就是黑色
- ❓ 如果没有第3个条件,红黑树就不厉害了?但是不是默认是黑色的吗
调整策略
插入调整和删除调整是分开的 [与AVL树不同]
<关键点>
①【插入调整,要站在祖父结点看】
- 向下看两层
- 某结点与其子结点发生冲突时,某结点管不了
- “隔代亲”:爷爷管儿子和孙子的事,不允许儿子打孙子
- 插入的结点一定是红色,基于5th条件
- ❌插入黑色——必然会调整 [一定会改变某条路径上黑色结点的数量]
- ✅插入红色——可能会调整
- [插入调整的目的] 解决双红情况
②【删除调整,要站在父结点看】
- 向下看一层
- 发生的前提
- 删除黑色 [参考二叉排序树的删除]
- 度为0⭐:特例 [NIL起作用了]
- 会产生一个双重黑的NIL结点
- 触发删除调整
- 度为1
- 其唯一子孩子肯定是红色,否则该结点一定会有另一棵子树,来保证左右两侧的黑色结点数量相等,与度为1矛盾
- 不会触发删除调整
- 度为2:可转化为度为0或1的情况
- 度为0⭐:特例 [NIL起作用了]
- 删除红色:不影响平衡状态
- 删除黑色 [参考二叉排序树的删除]
- [删除调整的目的] 解决双黑情况
-->总共5种情况:插入2种 + 删除3种
- ⭐关键关键⭐ ——通用的调整策略
- 把每一种情况,想象成一棵大的红黑树中的局部子树
- 根结点可能还有“长辈结点”,其它结点可能还有子树
- 为了不影响全局,局部子树的黑色结点数量在调整前、后相等
- [下面的每一种情况展现的都只是树的一部分]
- 把每一种情况,想象成一棵大的红黑树中的局部子树
- [PS] 如果根结点不是黑色,染个色就完事了 [不重要]
插入调整
[目标] 解决双红情况
两大类情况:4 + 4 种小情况
情况一
-

- 【特点】叔叔结点为红色
- 【策略】
- 修改三元组<15[1, 20]>的小帽子
- 黑红红👉红黑黑:爷爷抢爸爸们的红帽子
- 保证各路径的黑色结点数量不变
- 修改三元组<15[1, 20]>的小帽子
- 【图示】红色上浮
-

- [PS]
- [图中]根结点的颜色一定是黑色,否则插入前根结点和子结点冲突,不平衡
- 包含4种小情况:插入结点
x可以有四种位置,但处理方式一致
情况二
示例:LL
-

- 【特点】叔叔结点为黑色,冲突发生在LL [两个红色结点在L和LL]
- 【策略】
- 先使用AVL树的旋转调整策略:LL [示例]、LR、RL、RR
- 再修改三元组的颜色:红色上浮 [红黑黑] or 红色下沉 [黑红红]
- 【分析】图中<LL型失衡>,哪些结点是确定[存在+颜色]的?哪些是特例?
-

- 确定 [蓝框框定]
- LL型 → 10、15
- 情况二 → 25
- 15是红色 → 20
- 每条路径黑色结点数量相同[2个] && 10、15是红色 → 5、13、19
- [PS] 4个黑色结点都是NIL也行
- 特例
- 17
- 可红
- 可无、可黑 [但不可包括在图中,否则不满足5th条件]
- 17
-
- 【图示】大右旋 + 红色上浮/下沉
-

- LL型经大右旋后,黑色结点数量变化导致不平衡👉使用 [红色上浮/下沉] 调整
-
- [PS]
- 针对两个红色结点的旋转,不影响每条路径上的黑色结点数量
- 对于小左旋、小右旋
- 举例:[原图假设] 抓着15号结点小右旋
- 所以小旋不会影响平衡
- ❗ 插入结点
x的位置是回溯调整的中间结果,并不是直接插入后的样子 - 包含4种小情况:LL、LR、RL、RR
- 针对两个红色结点的旋转,不影响每条路径上的黑色结点数量
删除调整
[目标] 解决双黑情况
两大类情况:兄弟结点为黑色 [2 + 2 + 2种小情况]、兄弟结点为红色 [特殊情况]
情况一
示例:双黑子结点在右侧
-

- 【特点】双重黑结点x的兄弟结点是黑色,兄弟结点的两个子结点也是黑色
- 【策略】父结点增加1重黑,双重黑结点与兄弟结点减少1重黑
- [PS] 95是回溯过来的 [看问题的格局要大]
情况二
示例:RL
-

- [注意观察双黑结点x的位置,关注38为根结点的子树]
- 【特点】兄弟结点在右侧 + 兄弟结点的左子结点是红色,且右子结点一定是黑色 [否则判断为RR型,见后]
- 【策略】小右旋 ,原兄弟结点改成红色,新兄弟结点改成黑色,转变成RR型 [见情况三]
- 【分析】哪些结点的颜色是确定的?[小右旋部分]
-

- [参照原图,蓝框框定为确定颜色]
- RL型 → 72、51、85
- 根为38的子树的每条路径黑色结点数量相同[2个] && 51是红色 → 48、64
-
情况三
示例:RR
-

- [注意观察双黑结点x的位置,关注38为根结点的子树]
- 【特点】兄弟结点在右侧 + 其右子结点是红色 [左子结点不做要求]
- 【策略】大左旋,新根结点等于原根结点 [双黑结点的父结点] 的颜色,两个新的子结点改为黑色,双黑结点减少1重黑 [此顺序无讲究]
- 【分析】哪些结点的颜色是确定的?
-

- [参照原图,蓝框框定为确定颜色]
- RR型 → 28、 51、72
- 每条路径黑色结点数量相同[≈2个,38不确定] && 72是红色 → 64、85
- [PS] 38、48不确定
-
- 【思考1】颜色修改策略
- 首先因为48有可能是红色,为了避免可能的冲突 ❗,只能将38改为黑色
- 接下来,为了保证局部子树的黑色结点数量在调整前、后相等
- ① [2个] 如果38本来是红色 → 51改为红色,72改为黑色
- ② [3个] 如果38本来是黑色 → 72改为黑色
- 【通用方式】新根结点等于原根的颜色,新的子结点都改为黑色
- 黑红红👉红黑黑
- (或者)
- 黑黑红👉黑黑黑
- 【思考2】为什么要通过左旋解决双黑?
- 大左旋后,可以让双黑所在路径上多一个黑结点 [51的加入],所以双黑可以减一
- 否则,平白无故的给双黑减一,在哪里可以保证给路径上黑色结点数量加一呢
- 大左旋后,可以让双黑所在路径上多一个黑结点 [51的加入],所以双黑可以减一
情况二、三小结
- 情况二:RL、LR;情况三:RR、LL
- 双重黑结点的兄弟结点是黑色,且兄弟结点中有红色子结点
- RR[兄弟结点在右侧 ➕ 其右子结点是红色]
- 大左旋,新根改成原根的颜色,新根的两个子结点改成黑色
- RL[兄弟结点在右侧 ➕ 其左子结点是红色,且右子结点一定是黑色]
- 小右旋,原兄弟结点改成红色,新兄弟结点改成黑色,再进行RR策略
- LL、LR:类同RR、RL
- RR[兄弟结点在右侧 ➕ 其右子结点是红色]
- 优先级:RR > RL,LL > LR
特殊情况
- 【特点】双黑结点的兄弟结点是红色
- 【策略】抓着双黑结点的父结点,向双黑结点旋转,原根结点改为红色,新根结点改为黑色
- 【图示】大左旋 + 原/新根结点换色
-

- 蓝框是确定颜色的结点,如何确定的?
- 特殊情况 → 双黑结点、兄弟结点
- 4th条件 && 兄弟结点是红色 → 父结点
- 5th条件 && 兄弟结点是红色 → 兄弟结点的子结点 [再往后黑色结点位置不一定要连续]
-
- 【转换后】站在原根结点往下看,做删除调整
- 此时,双重结点的兄弟结点一定是黑色,即可转到情况一、二、三
代码演示
插入调整

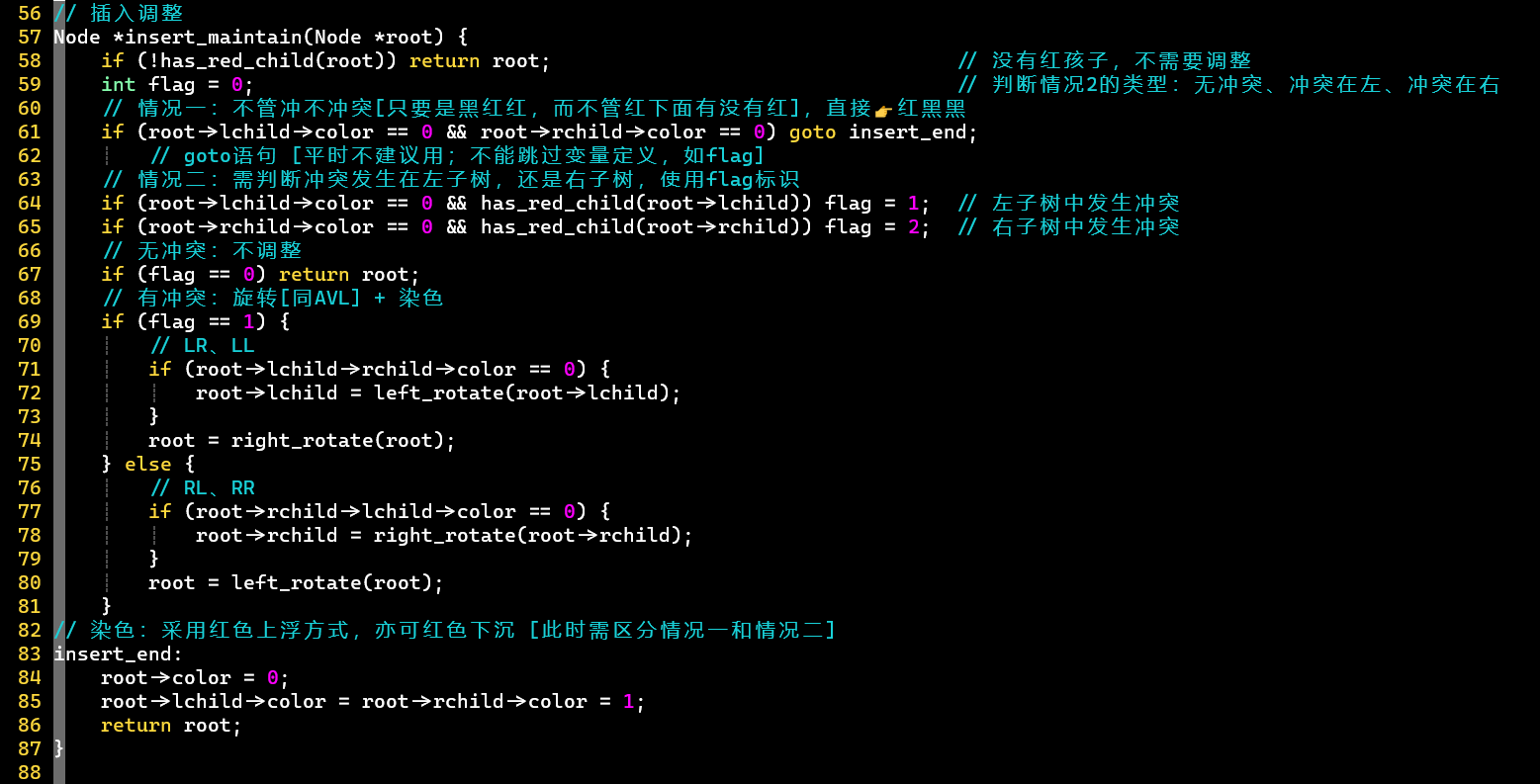


- 根结点的手动染黑
- 保证2nd条件:根结点为黑色
- 什么情况下,根结点会为红色
- 插入的第一个结点 [插入的结点为红色]
- 情况一的红色上浮
- 情况二的红色上浮 [红色下沉则不会影响]
- ❗ 只有手动染黑操作,会增加路径上黑色结点的数量
- 在根结点处发生大旋转操作时,根结点会变成红结点,此时手动染黑生效
- 通过代码封装处理:insert = __insert + 染黑
- ❓ 情况一的偷懒操作对回溯时的调整有没有影响?
- 不会对下面的路径产生冲突
- 不影响路径的黑色结点数量
- 可能会导致上层结点发生冲突
- 但本身就是随机操作,当红黑树到了一定规模时,损耗可忽略不计
- ❓ 红色下沉和红色上浮的区别:各有各的好,都有冲突的可能
- 红色下沉:容易和新插入的结点产生冲突
- 红色上浮:容易和父结点产生冲突
- [PS] 红黑树很大的时候,红色结点很难上浮
- ❓ AVL树与红黑树
- AVL树比红黑树更平衡
- 红黑树调整的代价低于AVL树
- 红黑树约一半的调整都可以通过染色解决 [情况一]
- 适合动态插入和删除结点,而查找可能稍逊于AVL
- [PS]
- 插入调整,发生在递归的回溯阶段
- 插入调整的代码中,使用goto语句,减少了代码量;使用函数封装应该更标准
- [结果示例]
-
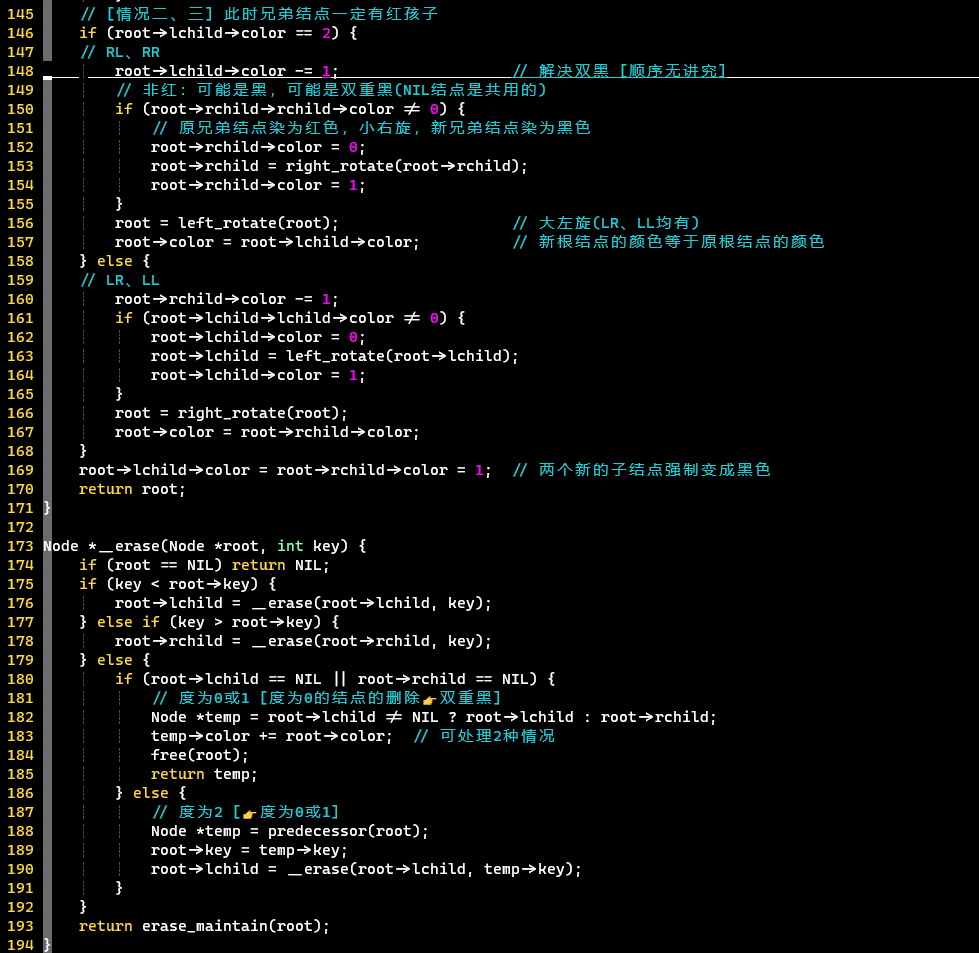
删除调整
-

-
-

-
-
在插入调整代码的基础上增加
-
删除调整情况分为【无双黑子结点】+【有双黑子结点 [特殊情况 + 三种情况 (兄弟结点无 / 有红孩子 <LR、LL、RL、RR>)]】
-
情况二、三,记得解决双黑问题,顺序无讲究
-
进行LR / RL类型判断的时候,不能直接判断LL子树是否为黑色
- 可能是黑色,也可能是双重黑
- [双重黑] 因为LL可能是NIL结点,而NIL结点在内存中是共用的,其颜色可能是双重黑
- 【判断转变】判断LL子树是黑色 👉不是红色
-
main函数添加删除操作
-
[结果示例]
-

- 演示了三种情况,结果见列表
- NIL在内存中是共用的,可能都是双重黑
-
[PS] 经过一代船长的提炼,红黑树从无到讲,所花时间不到4小时,代码量不到200行
随堂练习
HZOJ-64:海贼红黑树

样例输入
1 1
1 2
1 3
3 0
2 2
3 0
样例输出
1 1 0 0
2 1 1 3
3 1 0 0
1 1 0 3
3 0 0 0
- 基于代码演示部分的最终代码,① 调整输入输出
- ② 并修改插入调整中对情况一的调整策略 [偷懒->不偷懒]
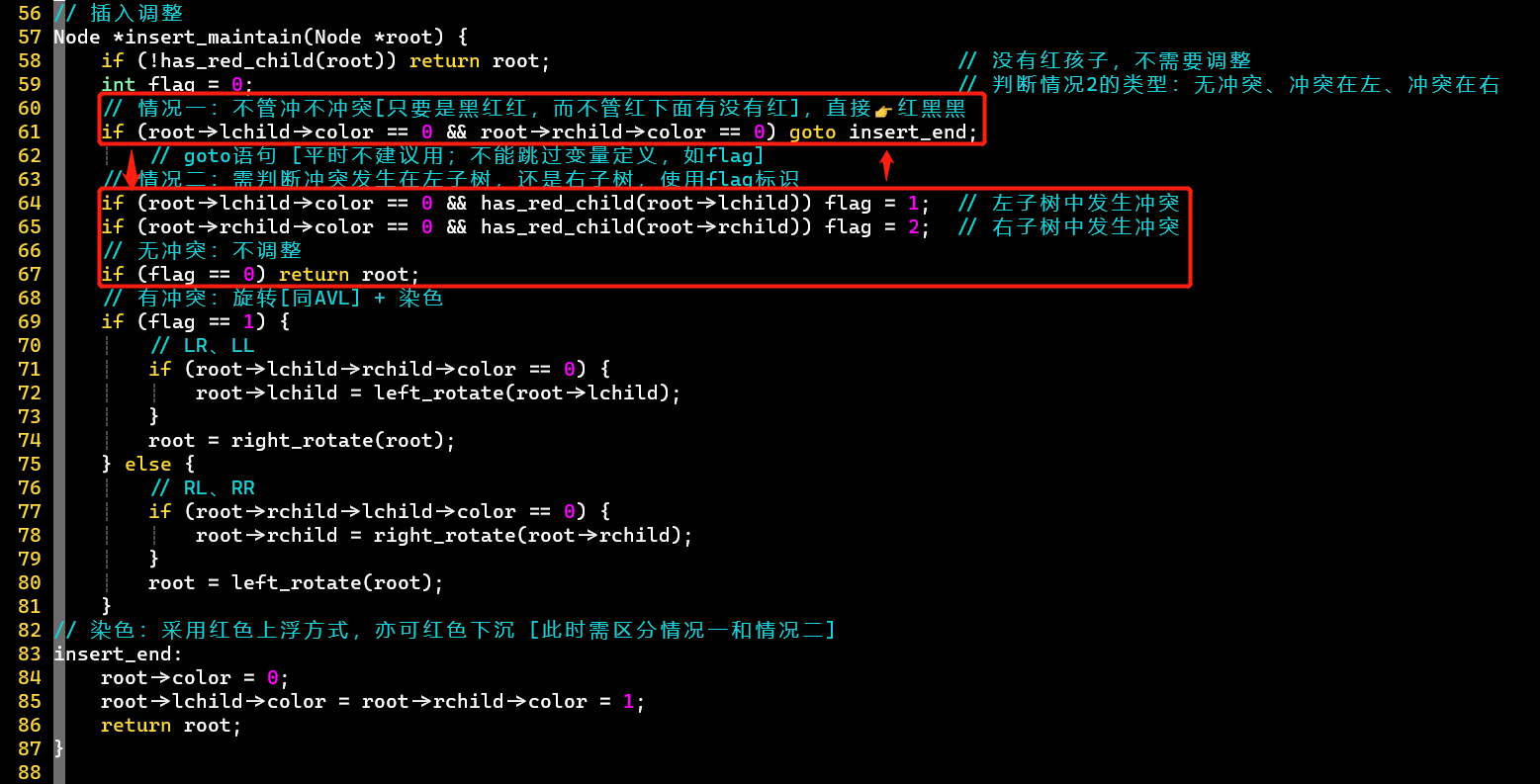
- 将两部分代码对调,即先判断是否产生了冲突,如果有冲突,再区分情况一和情况二
附加知识点
- ⭐分析调整策略时,要清楚哪些点的颜色是确定的
- 其重要性等同于AVL树的调整策略中,对树高的把握
- 重点是思考过程!而不仅仅是调整策略
Tips
- 编码技能是一套独立的技能,与算法数据结构思维是相互独立的,所以不是理论知识的简单重复
- 当你不把自己的时间当成金钱,那就很难完成阶层的跃迁
- 下节课预习:哈夫曼树 [+哈夫曼编码]、字符串匹配算法 [预习KMP]




