一些经典、绝伦的单模匹配相关算法
课程内容
相关定义
单模匹配问题:在文本串中查找某个模式串是否出现过
多模匹配问题:查找多个模式串
文本串/母串:被查找串
模式串:待查找串
文本串长度为,模式串长度为
暴力匹配法
所有字符串匹配算法的基石
思想
- 依次对齐模式串和文本串的每一位,直到完全匹配
- 其思想是理解所有匹配算法的基础:不漏的找到答案
- 而其他算法优化的核心就是不重,减少重复的、不可能匹配成功的尝试
- 时间复杂度:
引发思考
第一次失配时,暴力匹配是怎么处理的?
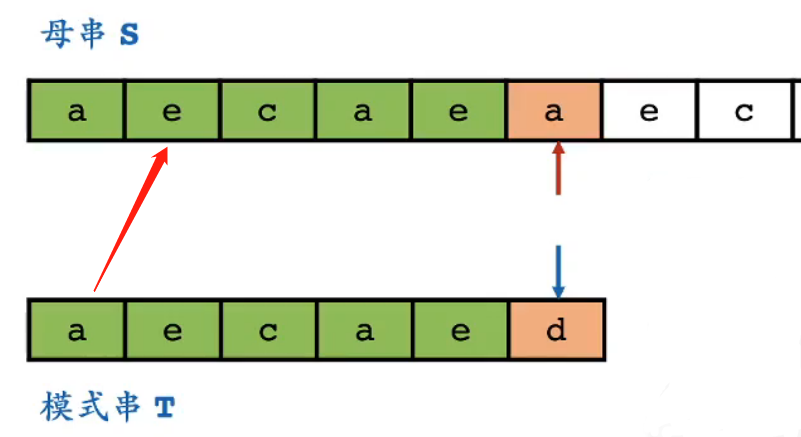
- 它会用模式串第一位与母串的第二位进行匹配
- 而如果匹配成功,意味着模式串第一位与文本串第二位相等
- 因为已知模式串的第二位与文本串的第二位是匹配成功的
- 那么必然存在,模式串的第二位与第一位相等
- 模式串的第二位与第一位是否相等,其实在拿到模式串时就可以知道
- 对于上图,完全没有必要尝试用模式串第1位与母串第2位进行匹配
- 它们肯定不匹配
- 是否可以跳过肯定不匹配的位置,KMP算法有自己的想法
KMP
状态机思想、自身结构重复展开概念
思考过程
接上,关注A、B、C位置
-
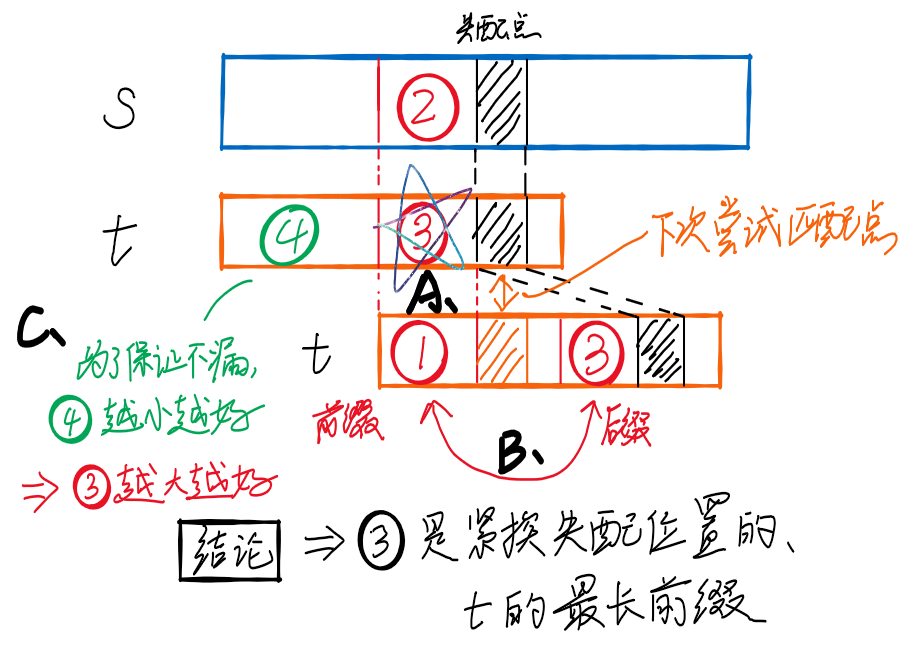
- 【假设】在黑色阴影处失配时,模式串往后移动④的大小,此时文本串的②和模式串的①匹配成功的情况
- 【关键】第③部分:其左边界决定往后移动的距离 [同第①部分右边界]
- 【A】在这一竖列上,一定存在②=③=①,②紧挨着失配位置 👉 ③也紧挨着失配位置
- 【B】③实际是的后缀,①是的前缀 👉 ③等于的某个前缀
- 【C】为了保证不漏匹配,④应该尽可能的小 👉 ③应该尽可能的大
- 【结论】综上所述,通过③可以加速匹配过程,而③是紧挨失配位置的、的最长前缀
问题转换
预先得到失配时对应的③的大小,也是①的大小
-
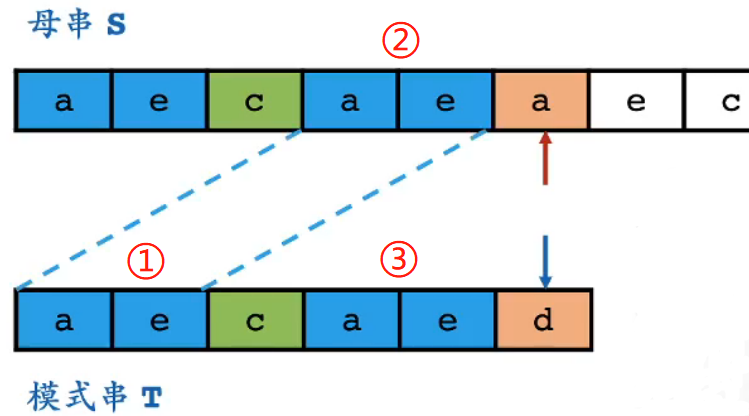
- 寻找模式串的①和③,用①后面的绿色字符去匹配②后面失配位置的橙色字符
- 要考虑模式串的每一位:因为失配的位置可能是模式串的每一位
- 模式串是预先知道的;文本串是不知道的、不可控的
- 👉 模式串的数组
next数组
- :当位置匹配成功,但位置失配时使用,作为模式串下一次尝试匹配的偏移
- 状态定义:以位置结尾的后缀中,可以匹配的最长前缀的下标 [右边界]
-
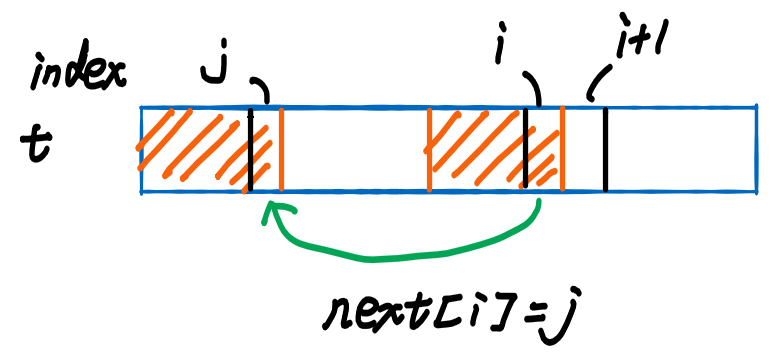
- 只针对模式串
-
- 转移公式:看图理解,关注图中①②处
-
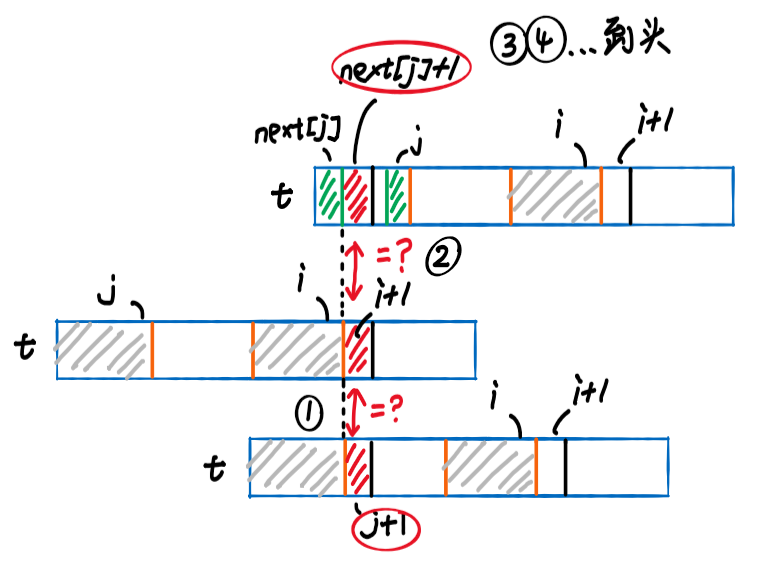
- 先看第二、三行,判断①
- 如果,则对应的最长前缀为
- 否则,将再向右移动尽可能短的距离 [类似上文思考过程中的④],也就是找到子串中,以结尾的后缀中,对应的最大前缀 [这就是数组定义]
- 观察第一、二行,判断②
- 如果,则对应的最长前缀为,其中
- 否则,继续将右移,判断③④...直到满足等于关系,或者不能再右移
- 涉及动态规划的思想,可跳转《面试笔试算法下》——1 从递推到动态规划(上)
- 练习理解
- 定义虚拟位置:-1 [当匹配不到任何前缀时,值为-1]
- 练习1
-
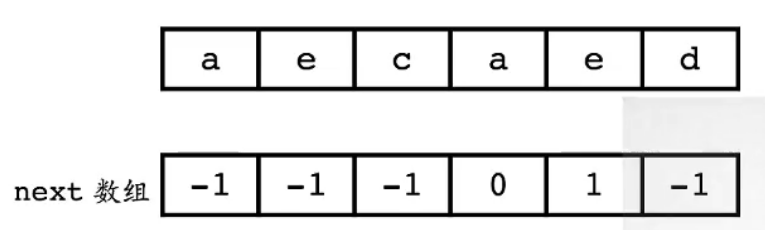
- 练习2
-
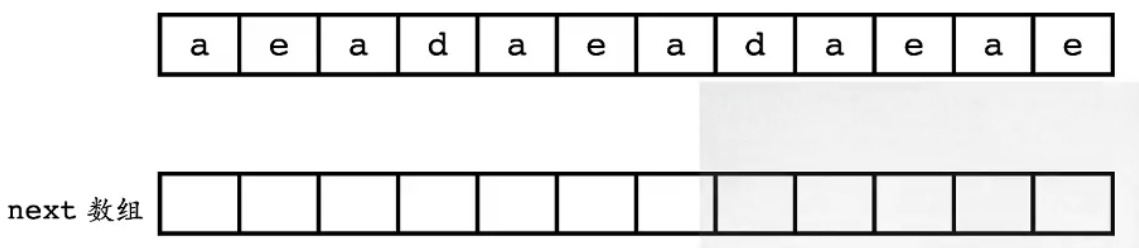
- 答案:
-1、-1、0、-1、0、1、2、3、4、5、6、1
- [PS] 参考KMP算法详解——CSDN
- 文中数组定义为:前缀和后缀的最大公共长度[不包括字符串本身,否则最大长度始终是字符串本身]
- 可见数组的定义不唯一
- 自身结构重复展开概念,求数组时就有这个思想
匹配过程
- 依次遍历文本串的每一位
- 从模式串起始位开始匹配
- 如果文本串的当前位置与模式串的当前位置相等,则匹配模式串的下一位
- 否则,根据数组不断前移模式串的尝试匹配位置,直到相等条件成立,匹配模式串的下一位;或者不能再前移,匹配文本串的下一位
- 当成功匹配到模式串的结尾时,输出文本串对应匹配的位置;或者没有找到
小结
- 理解模式串中的第③部分的重要性 [见思考过程]
- 加快匹配速度的核心,避免掉大量无用的匹配尝试
- 保证不漏的核心:第③部分匹配到的是模式串的最长前缀
- 可以从状态机的角度理解,见代码演示——状态机版KMP
- 时间复杂度:
- [PS] KMP还存在一些优化方法
SUNDAY
先找腚,再找头
模拟操作
直接模拟一遍如下情况
- ① 当发生失配时,观察模式串末尾对应母串位置的后一位e——黄金对齐点位
-
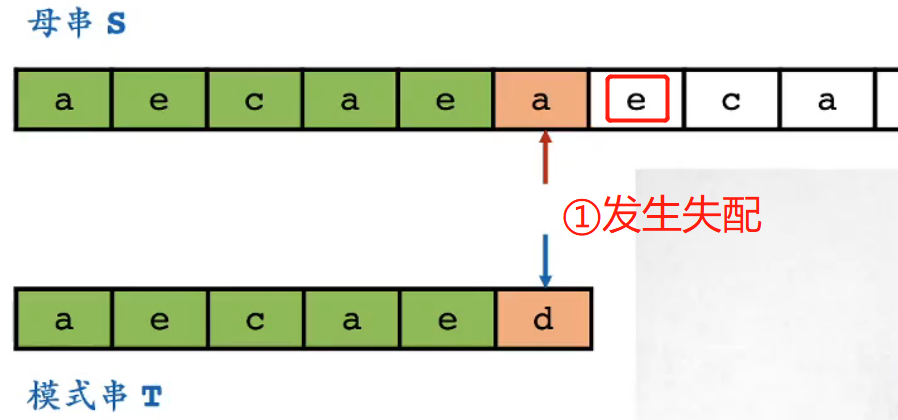
- [注意] 不是观察失配位置后一位 <不要被图误解>
-
- ② 在模式串中,从后向前找第一个e的位置
-
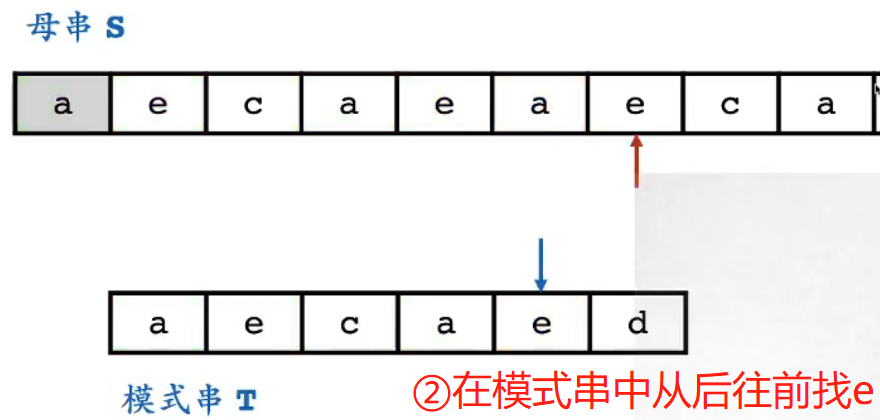
- 在倒数第2位找到e
-
- ③ 倒数第2位意味着,模式串对母串的尝试匹配位置向右移动正数2位,然后重头尝试匹配母串
-
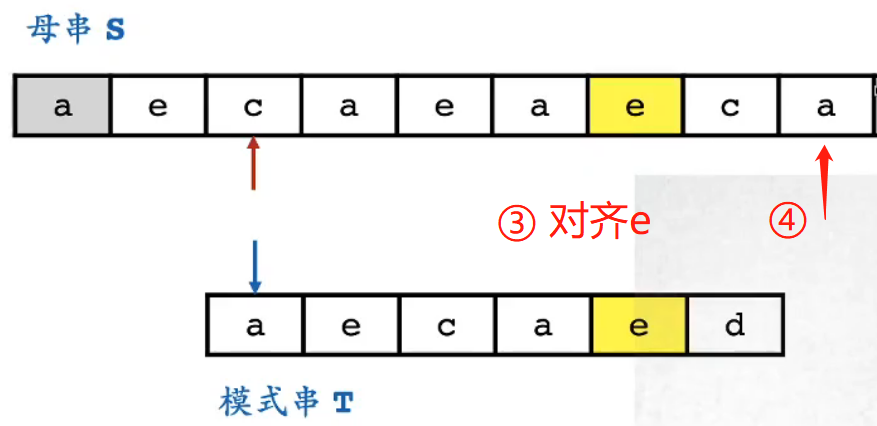
- [个人理解] 如果该右移要匹配成功,e位置必须对齐,因为总会经过e;找第一个e,是为了不漏答案
-
- ④ 上图仍然发生失配,此时再在模式串中,从后往前找第一个a,再对齐,匹配...直到成功匹配,或者匹配结束
- [PS] 如果找不到黄金对齐点位对应的字符,则右移的偏移量为整个模式串的长度+1
流程
- 预处理每一个字符在模式串中最后一次出现的位置
- 模拟暴力匹配算法过程,失配的时候,文本串指针根据上述预处理信息,向后移动相应位,然后重新匹配
- 最终,匹配成功返回下标,或者找不到
小结
- 核心:理解黄金对齐点位 [详见模拟操作]
- 如果匹配成功,其一定会出现在模式串中
- 其应该和模式串中最后一个出现该字符的位置对齐
- 右移操作:所找字符出现在模式串的倒数第几位,就将文本串指针右移几位
- 最快时间复杂度:
- 对应场景:要寻找的黄金对齐点位字符,在模式串中没有找到,文本串指针将向后移动整个模式串长度的距离
- [PS]
- 最坏时间复杂度:,但此种情况对应的字符串一般没有实际意义
- 使用场景:解决“一篇文章中查找一个单词”等简单的单模匹配问题 <工业中很常用>
- 对比KMP
- SUNDAY更好理解与实现
- 但KMP算法的思维方式更高级,应该学习 [状态机]
SHIFT-AND
非常优美的小众算法,考察想象力
状态机思想:NFA,非确定性有穷状态自动机
编码数组d
⭐将模式串转换为一种编码,转换完后匹配问题就和模式串没有一毛钱关系了
-
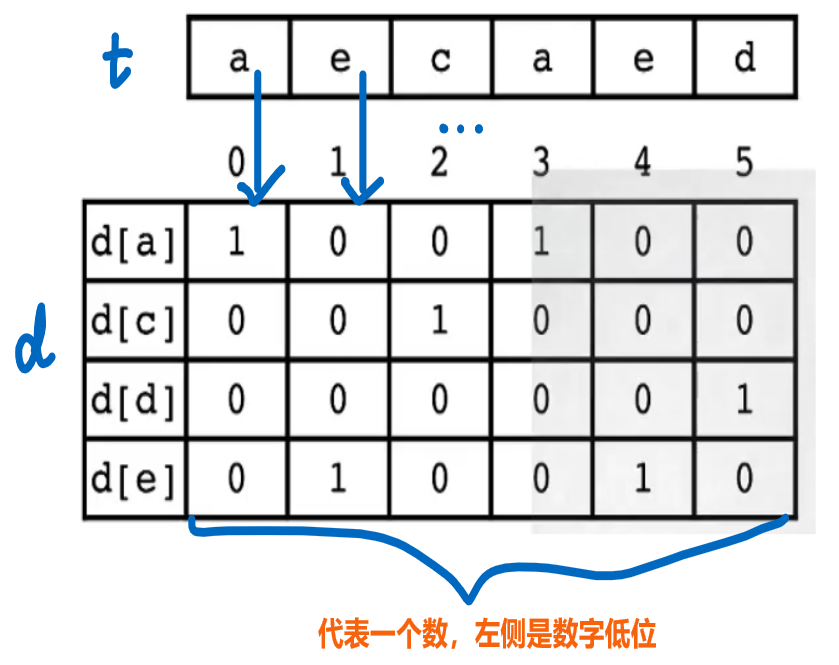
- 从第0位开始,依次读取模式串t的每一位
- 当在第0位出现'a'字符时,将数组中下标为'a'的元素第0位置1
- 当在第1位出现'e'字符时,将数组中下标为'e'的元素第1位置1
- 以此类推,得到数组
- [PS]
- 数组下标可以对应字符的ASCII码
- 数组元素可以存储int类型 [32位]、long long类型或者自定义类型,这决定可匹配的最长模式串长度
- 注意字符串序和数组元素的数字序,第0位字符对应后者的低位
状态信息p
理解状态定义,感受转移状态
- 状态定义:
- 在的二进制表示中,如果第位为1,则代表以文本串结尾时,可以成功匹配模式串的前位
- 图解,对照上述定义与下面的三对圆圈
-
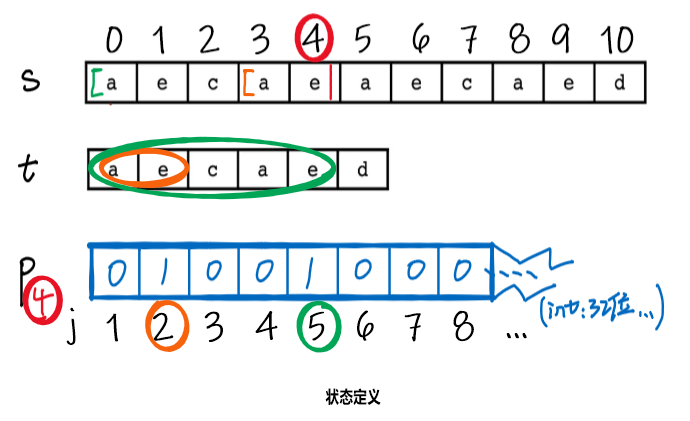
- 红色:代表以文本串结尾,为现在的匹配条件
- 橙色:的第2位为1,代表模式串的前2位可以满足上面匹配条件,即与匹配
- 绿色:的第5位为1,代表模式串的前5位可以满足上面匹配条件,即与匹配
- [PS]
- 的二进制长度取决于使用什么数据类型,同数组元素,如int:32位
- 暂不关注是如何来的,稍后看转移过程
-
- ⭐由此可见
- 中同时存储着多个匹配结果的信息❗
- 当的第位为1时,匹配成功,即
- 匹配位置为:
- 转移过程:
- ⭐关键公式⭐
- 此时已完全抛开模式串,通过的上一个状态和数组,即可得此时的值
- 原理分析,对照关键公式和下图的①②
-
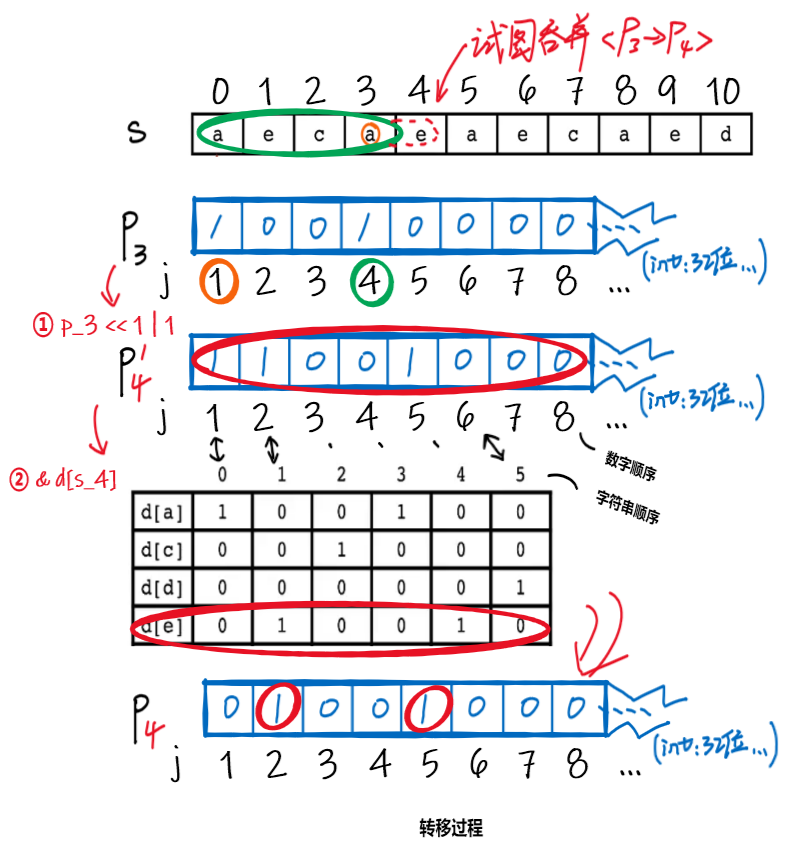
- 假设已知,当前可以匹配和
- ①左移1位+或1运算,得到过渡状态
- 左移1位:试图在前一个匹配基础上,吞并,即匹配和
- 匹配成功的条件在于后面的【与运算】
- [注意] 左移操作在图中表现为右移,因为数字顺序是低位在前
- 或1运算:留一个单独匹配的机会,匹配成功代表匹配这一个字符
- 左移1位:试图在前一个匹配基础上,吞并,即匹配和
- ②与运算
- 上面两个操作都只是尝试匹配,而真正成功与否取决于的表现
- 如果第位上与运算的结果为1,则代表成功匹配与
- 如、,匹配结果即状态定义部分的图解
-
- [PS]
- 的初始值为0,实际上是一个非确定性有穷状态自动机
- 习惯冲突:一般数字顺序右侧是低位,但在图中的左侧是低位;二进制数字最低位是1,字符串最低位是0;数组元素是数字,所以应该对应数字顺序,但上图是为了体现与模式串的对应位置关系,用的字符串顺序
- 准确理解的含义:上一次成功匹配4位,下一次才有可能成功匹配5位
- 对于多于64位的字符串匹配问题,需要自己创建数据类型
- 支持左移、或、与运算即可
- 再对应修改编码数组和状态信息的类型
小结
- ① 编码数组:将模式串中每一种字符出现的位置,转换成相应的二进制编码
- ② 状态信息:通过关键公式转移状态
- 时间复杂度:
- 完全不需要对模式串来回倒
- 但是严谨来说,不是纯,这和计算机的数据表示能力有关
- ❗ 可以解决正则表达式匹配问题
- 例如:
- ① 将上述模式串转换为编码数组
- 对于数组的每一纵列可以有多位,置1
- 即模式串的每一位可以让多个【数组的元素】的对应二进制位,置为1
- ② 之后就与模式串无关了,根据数组和关键公式解决问题
- [PS] 这里可以看出模式串之所以叫模式串,是因为它不只是指字符串,还可以是正则表达式(也可以看作一种有相关性的多模式)
代码演示
暴力匹配法
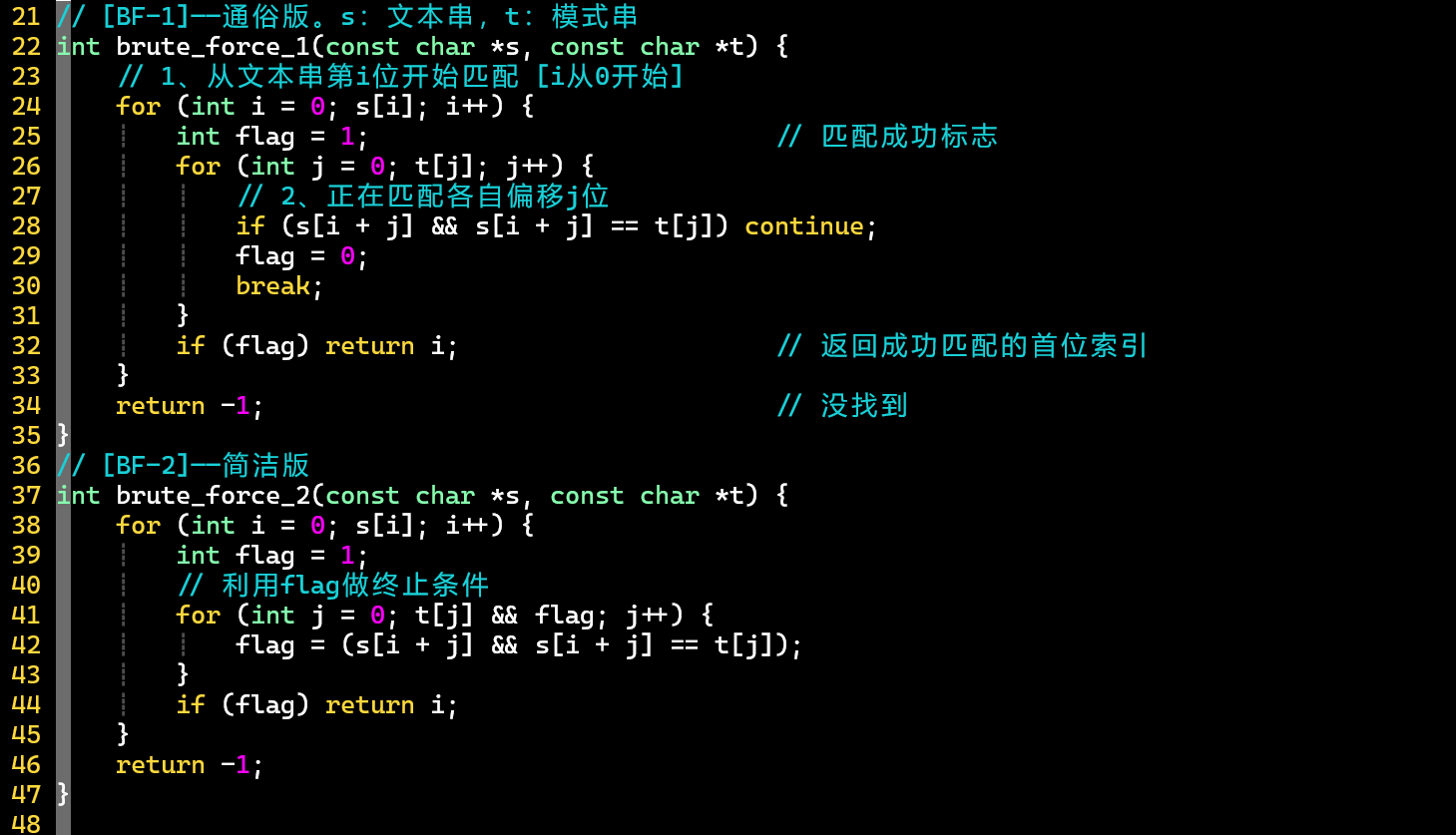
- 两种版本,学习简洁版的技巧,灵活运用
- 分别遍历文本串和模式串,逐位判等,若失配,将文本串指针右移一位
- 该思想是所有字符串匹配算法的基础
KMP
2种编程方式,后者更接近于算法的本质思想
- ① 普通编码:直接获得数组,再使用数组做失配偏移
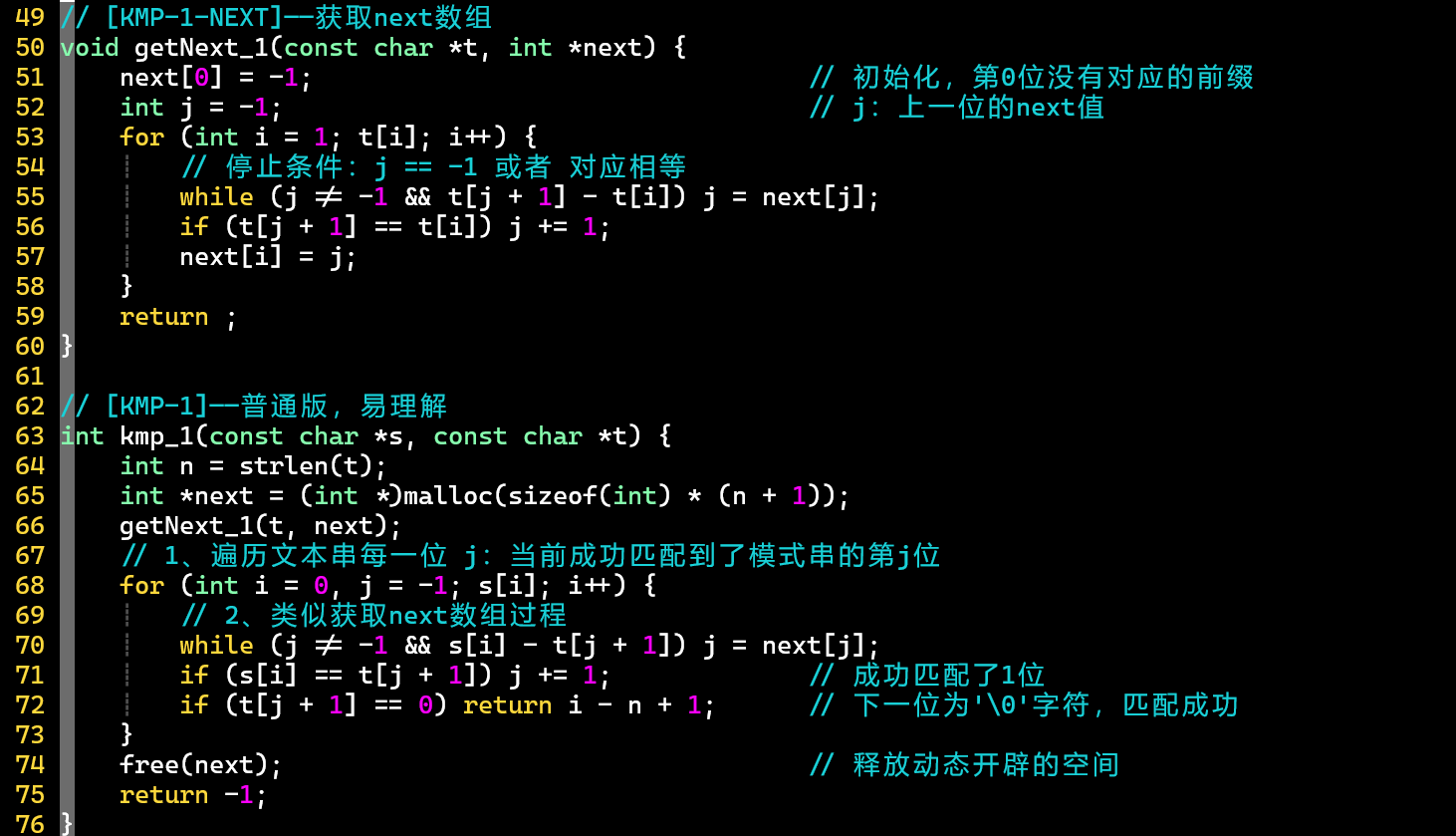
- 预处理数组→遍历文本串每一位→匹配模式串 [利用数组]
- ❗ 观察:获取数组的过程和匹配文本串的过程非常相似,基于状态机的思想,可将两部分整合
- ② 高级编程:基于状态机的思想,将获取值的过程转化成状态的改变过程
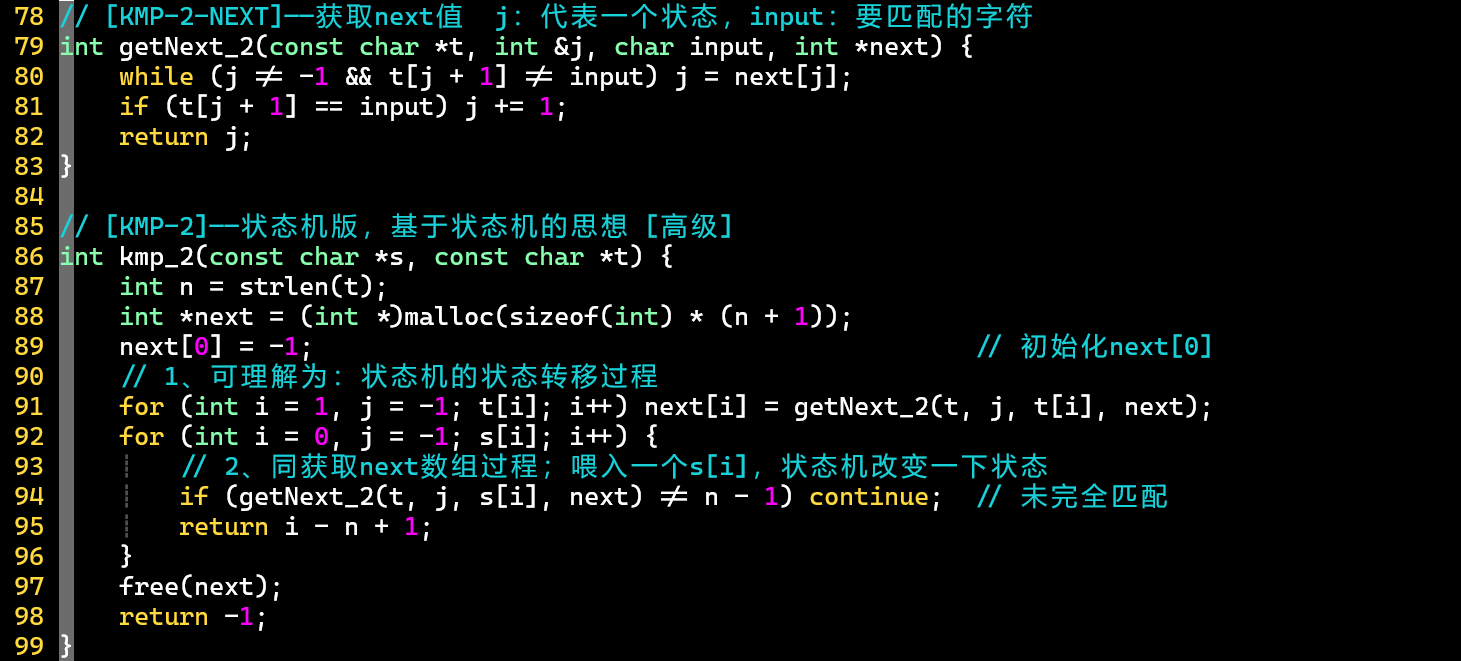
- 抽象化了一个状态机模型:所指向的就是状态机的位置,方法相当于根据输入字符,进行状态跳转,实际上就是改变的值
- 更接近KMP本质的思维方式
- PS:应该在匹配成功了返回前也对数组进行free
SUNDAY
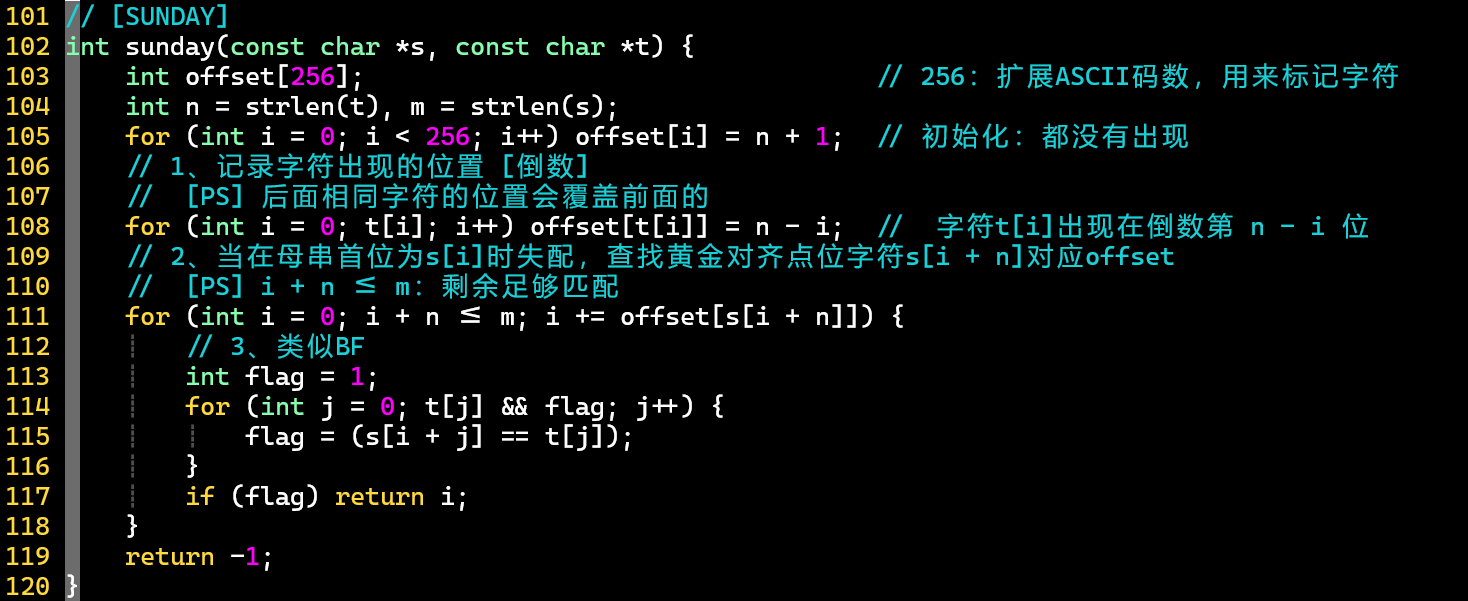
- ❗ 注意256的含义:用来记录每种字符在模式串中的位置
- 预处理数组的过程:先初始化为都没有出现的情况,表示文本串指针可以直接右移一个模式串长度+1的距离;在预处理过程中,后面相同字符出现的位置会覆盖前面的,正合SUNDAY意
- :黄金对齐点位对应的字符
- :合理地利用了、变量,表示文本串还够模式串匹配
- 相比KMP,SUNDAY更好理解,代码更好实现 [解决简单单模匹配问题的不二选择]
SHIFT-AND

- ⭐ 思想优美,代码简单
- 注意
- 与数字有关的数组元素和状态,最低位为1;而字符串对应为0
- 但转移过程是数字之间的运算,所以不用顾虑位置是否对齐
随堂练习
——Hash——
常用的解题套路
HZOJ-275:兔子与兔子

样例输入
aabbaabb
3
1 3 5 7
1 3 6 8
1 2 1 2
样例输出
Yes
No
Yes
- 思路
- 注意:查询次数特别多,查询区间非常大,暴力匹配一定超时
- 如何快速比较?👉 哈希匹配算法
- 通过哈希操作将字符串用数字 <哈希值> 表示
- 如果两个字符串对应的哈希值不同,两个字符串一定不相等
- 这样就剔除了大部分不相等的情况,而不需要再按位比较了
- 否则,再通过暴力匹配验证字符串是否相等
- 如果两个字符串相等,一次匹配就能成功
- [PS]
- 长字符串直接对应的哈希值可能太大,所以一般通过取余操作缩小哈希值
- 余数不一样 👉 字符串肯定不一样
- 设计哈希函数 [字符串->哈希值]
- :字符串的长度
- :第位字符对应的ASCII码值
- :位权 [素数]
- :模数 [素数]
- [PS] 字符在计算机底层是用二进制数字存储的
- ⭐本题中一个子串的哈希值
- 根据字符串与哈希值的关系,可以预先处理得到基于哈希的前缀和数组
- 从而得到子串基于哈希的区间和为
- 但是对于子串的哈希值,不应该包含子串在字符串中的位置信息、,即乘数因子应该从开始
- 所以,需要将区间和除以,但是对于取余运算,不能直接做除法,而需要借助逆元
- 最终子串的哈希值转换为
- :的逆元
- 逆元的快速求解请跳转到:快速求[模]逆元
- 根据字符串与哈希值的关系,可以预先处理得到基于哈希的前缀和数组
- 解题方式①
-
- 在文本串上,预先处理得到每一位基于哈希的前缀和,方便一会求区间和
-
- 通过区间和与逆元,求得某子串的哈希值:
-
- 比较两个子串的哈希值
- 如果不相等,子串一定不相同
- 否则,再用暴力匹配验证是否相同
- ❗ 两个子串不相同,但其哈希值相等的可能性为
-
- 解题方式②
- 基于方式①,设计两个哈希函数,对应、不同
- 比较两个子串对应的两个哈希值
- 都相等时,认定两个子串相同
- 否则,一定不相同
- ❗ 两个子串不相同,但其哈希值相等的可能性为
- 出错的概率极低,其实有很多算法都是概率性算法
- 代码
- 方式①:哈希匹配+暴力匹配
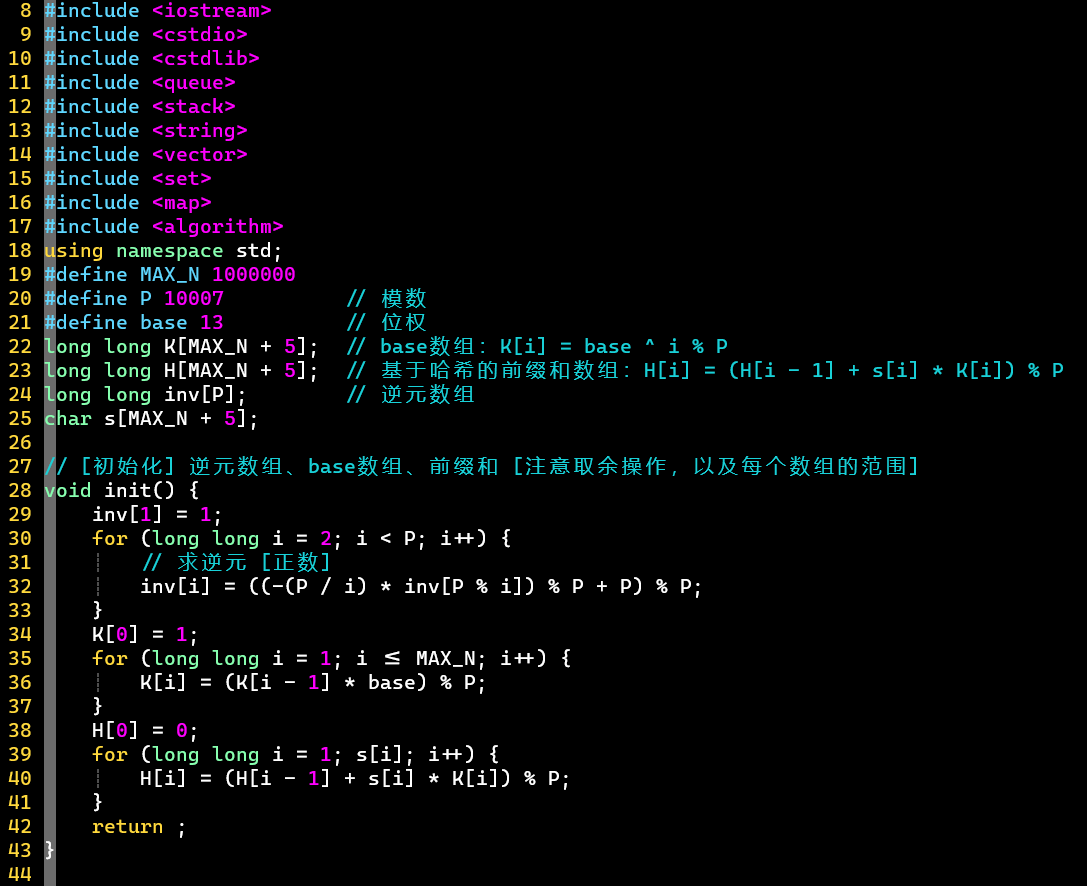
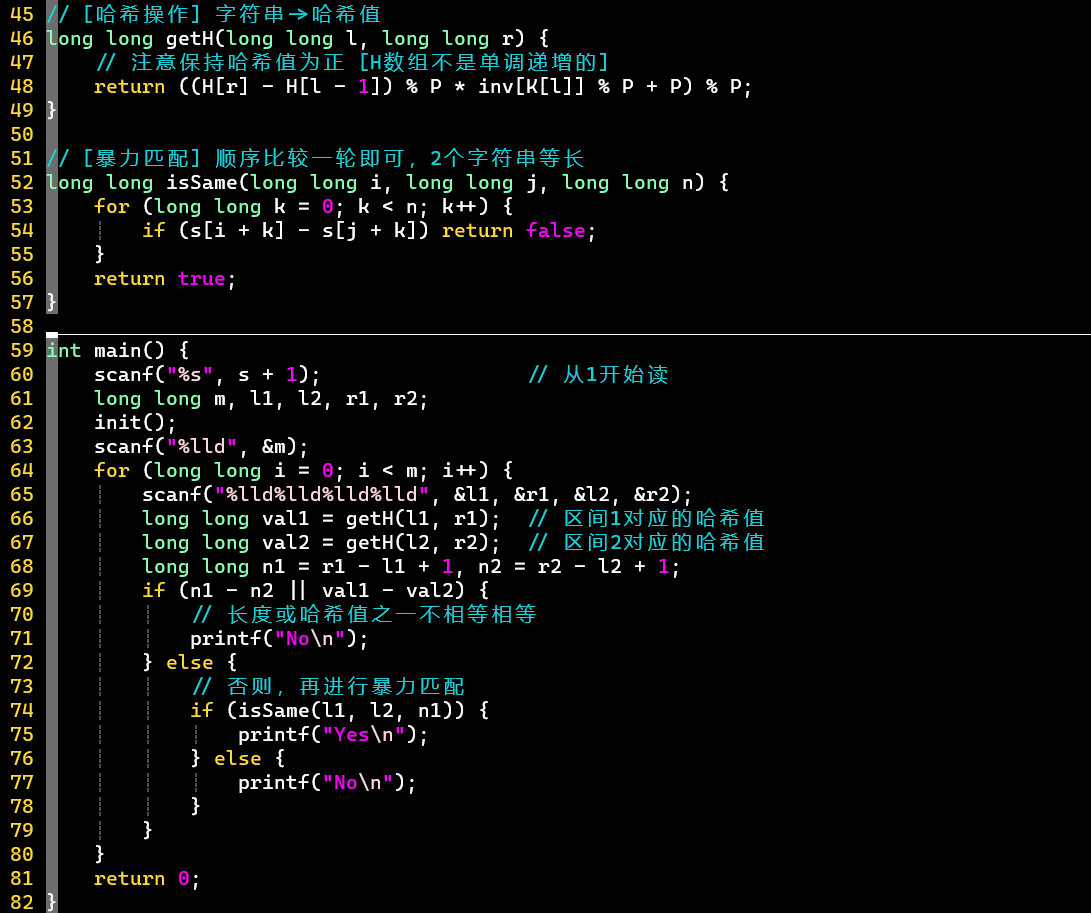
- ①值必须为素数,否则部分逆元没有意义,对应求出来的哈希值不正确
- 这会导致相同的子串也对应不同的哈希值
- 逆元存在的充分必要条件:互质
- ② 需要使用long long类型,中间过程的数值可能非常大
- 这会增大不同子串对应哈希值相同的概率,增加耗时 [暴力匹配]
- [PS]
- 时刻记得取余,防止数字超过表示范围,即使是long long
- 注意保证哈希值为正
- 基于哈希的前缀和数组不是单调递增的,因为求和时都有取余操作
- 值过小可能导致超时,暴力匹配次数过多
- 方式②:哈希匹配*2


- 注意:两个逆元数组分开初始化,保证初始化完全 [遍历的范围不一样]
- 或者使用相同的和不同的,可以一起初始化
- [PS] 为了保险,可以再加入暴力匹配验证
快速求[模]逆元
⭐推导过程
- 目标:求解中的
- [PS] 只考虑的情况,因为所有大于的都可以通过取余转换为小于的
- 令:
- 则:
- 最终将求的问题,转换为求的问题
- 而是模的余数,所以一定比更小
- 一个规模较大的问题 👉 一个规模较小的问题 [递推]
- 为保证逆元为正,再做一次处理
- [PS]
- 模逆元:逆元存在的充分必要条件是和互质
- 求逆元的方法很多,参考逆元知识普及(扫盲篇)——cnblogs
代码
-
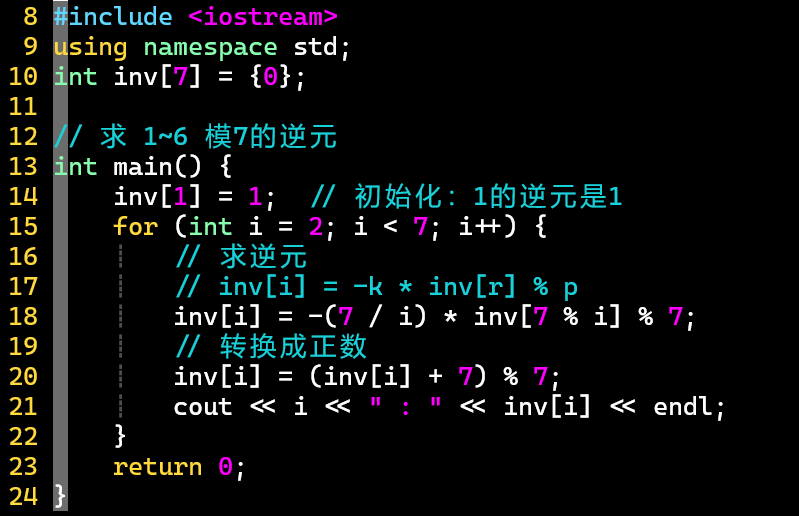
- 不管模数为几,1的逆元就是1 [初始化]
- 输出结果
-
- 可自行验证:原数与逆元相乘取余为1
-
附加知识点
- KMP、SHIFT-AND的本质思想:状态机 <在编译原理中会学到的知识>
- SUNDAY算法在生活中很常用,Hash匹配算法在解题中常用
- DFA、NFA是编译原理的知识
- 主要区别:DFA速度更快,NFA消耗内存更少
- 参考Difference between DFA and NFA——Stechies
Tips
- 上C++之前,一定先刷完预修课
- 成为算法领域里的内行,关键在提高自己的审美能力
- 生气是无能的表现,干正事!一步一步变好,不求一蹴而就


