多模匹配问题,与字符串匹配相关的数据结构
课程内容
多模匹配问题
有多个模式串的匹配问题,常规思路如下:
- Step1:多个模式串,建立成一棵字典树
- Step2:和文本串的每一位对齐匹配,模拟暴力匹配的过程
Trie
又名字典树、单词查找树,顾名思作用
看图理解
-
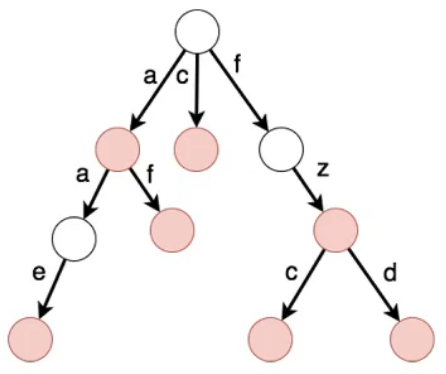
- 思考树的含义:结点代表集合,边代表关系
- 根结点可以理解为整个字典,第一个字母为'a'的单词放在第一个子树中,第一个字母为'c'的单词放在第二个子树中,以此类推
- 红色结点,代表从根结点到当前结点的路径上,经过的字母独立成词
- 当代表某字母的边存在时 [指向一个结点],表示存在以之前字母为前缀的单词集合
- [PS] 又名前缀树:每个字符串是按照前缀的顺序插入到该树形结构中的
常用场景
- ① 单词查找
- 根据代表某字母的边是否指向一个结点,判断某字母是否存在,从而查找一个单词
- ② 字符串排序
- 通过深度优先遍历一棵字典树,遇到成词标记输出字符串,即可完成字符串的有序输出
- 时间复杂度:,没有字符串大小比较
- ③ 多模匹配
- 一个字典树可以代表多个模式串,遍历文本串每一位,依次匹配字典树中的字符串,即可完成多模匹配
- 但该方式本质上是多模匹配下的暴力匹配方式
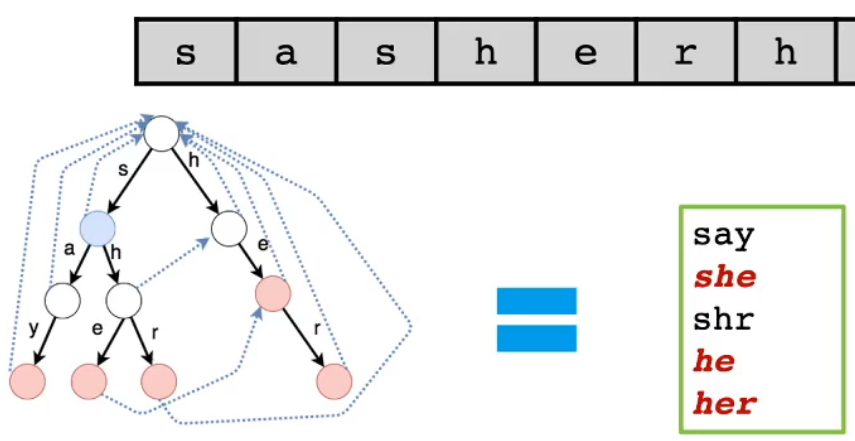
暴力匹配下的思考
-
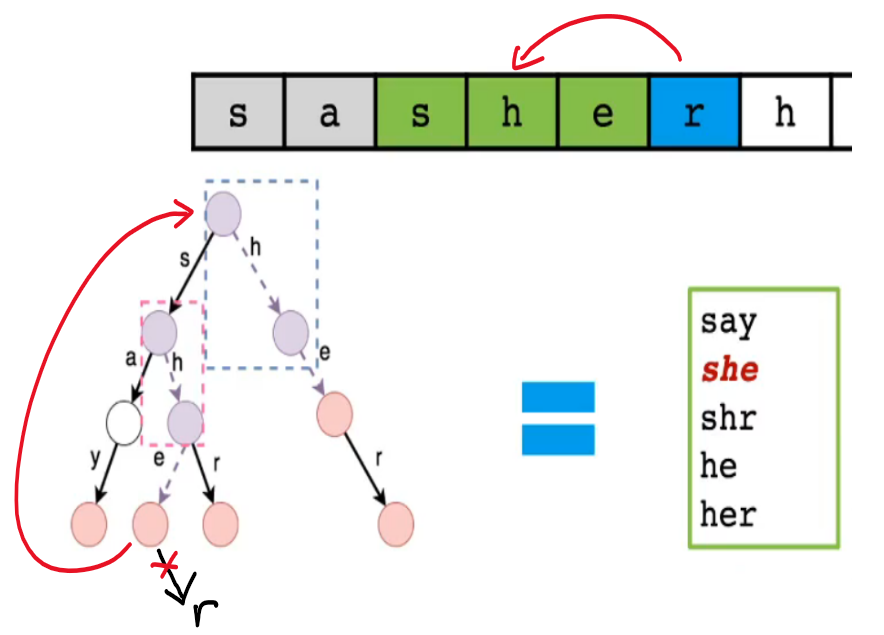
- 首先思考暴力匹配过程
- 当使用字典树成功匹配了文本串的"she"后,字典树再向下走一位,尝试匹配文本串的后一位'r'
- 但此时字典树下面已经没有结点了,匹配失败
- 文本串指针回溯到'h',字典树指针回到根结点继续尝试匹配,然后再成功匹配"her"
- 上述过程有一个明显的重复匹配过程
- 在成功匹配了"she"后,其实等价成功匹配了"he"
- 所以在文本串指针后移一位时,实际上应该可以成功匹配"her"
- 这其中就包含一种等价匹配关系[见下图红线]
-
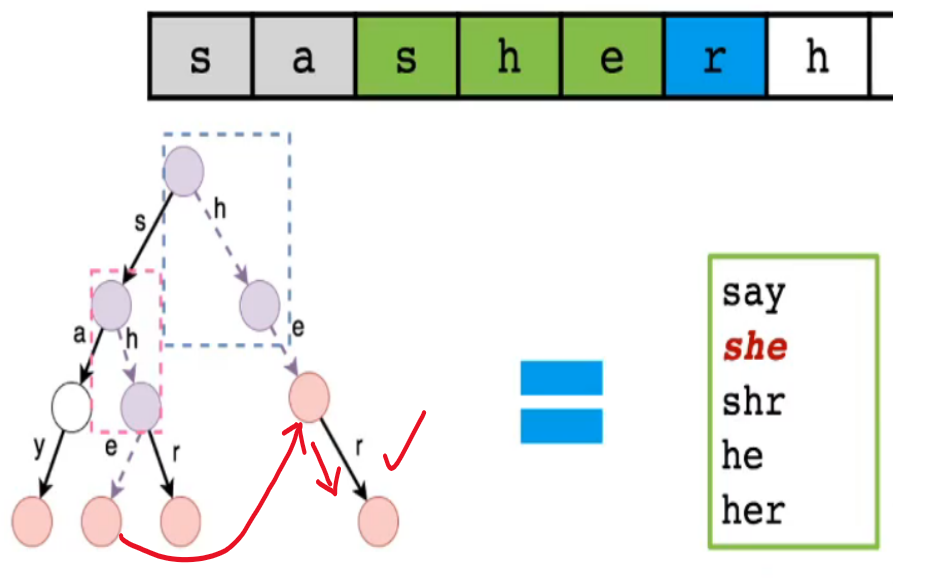
- 当字典树下方没有匹配的结点时,还可以看看等价匹配关系那边能不能匹配
- ❗ 是否可以通过等价匹配关系边加速匹配过程呢?AC自动机给出了答案 👇
-
AC自动机
状态机思想,解决多模匹配问题的效率问题
AC = Trie + fail [等价关系]
建立等价匹配关系
加速匹配过程
-
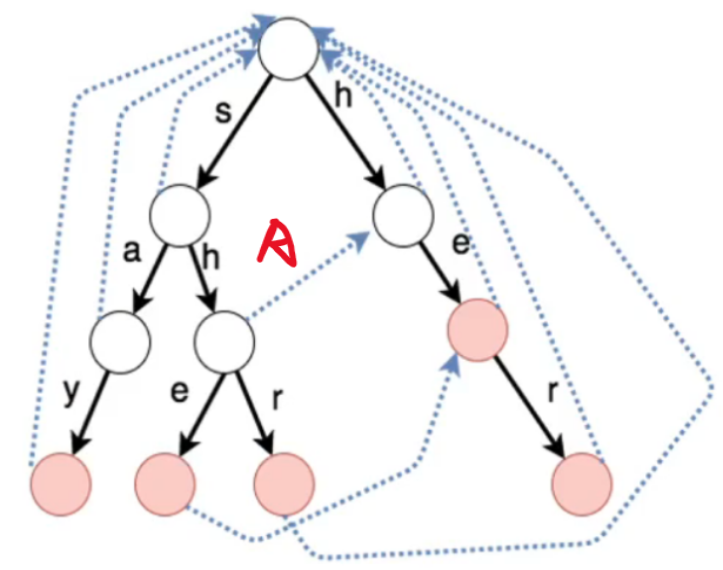
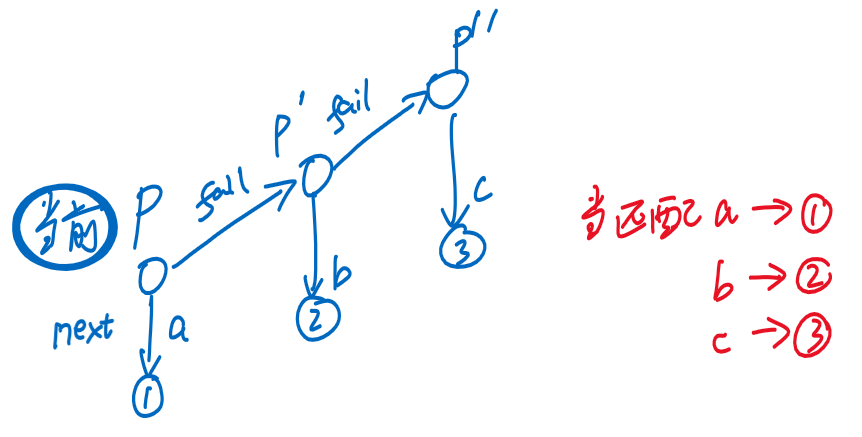
- ① 对于每一个子结点,其默认等价匹配关系是根结点
- ② 建立子结点的等价匹配关系时,会借助父结点的等价关系
- 如果找不到,还会往爷爷结点的等价关系找,直到到达根结点
- ❗ 不断往上找等价关系的思想和KMP中数组的建立思想一模一样,可跳转:《高级数据结构》——4 字符串匹配算法(上)
- 例如:在找's'->'h'的'h'的等价匹配关系时,会根据其父结点's'的等价匹配关系 [即根结点] 找等价匹配关系,而根结点下方恰好有'h',所以建立了等价匹配关系
- 注意
- 建立等价匹配关系时,要保证该结点上层的等价匹配关系已经建立,所以可以采用层序遍历的方式,使用队列
- 等价匹配关系通常叫做指针
匹配过程
在当前状态下匹配字符,匹配失败就到等价匹配关系上去匹配
- ① 状态转移
- 例如:"sas",在匹配第二个's'时匹配失败,所以会回到等价匹配关系——根结点,再次尝试匹配's';直到成功匹配,或等价匹配关系为空 [即根结点也找不到]
- [PS] 在程序实现中,根结点的等价匹配关系设为NULL更方便
- ② 取词
- 匹配到成词标记后,还需要往上判断等价匹配关系的成词标记
- 例如:当成功匹配文本串中的单词"she"时,也意味着成功匹配等价关系上的单词"he"
- 思考:此时的AC自动机,本质上是一个NFA[非确定性有穷自动机]
- [假设:"she"对应了字典树中的结点,"he"对应了字典树中的结点]
- 性质1:当前状态,在输入字符后,无法通过一步操作确定下一状态【满足】
- 性质2:当前状态,并不代表唯一状态 [也代表在状态]【满足】
- 时间复杂度:,有一个很大的常数
- 因为匹配过程中,通过等价关系向上跳的次数不固定
- 是否可以优化呢?基于路径压缩思想,见下
优化
让状态转移过程一步到位
- 思考:状态转移时,根据等价关系向上跳的过程,是否可以一步到位呢?
-
- 当前状态为,图左为的等价关系 []
- 在前面过程中,图右中的红色箭头→,需要通过指针做中间跳转
- 【目标】实现红色箭头的一步到位
-
- 优化:废物利用⭐
-
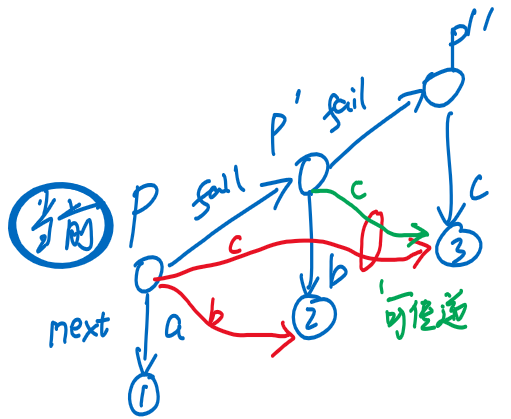
- 的数组中,和本来对应空结点,纯属浪费,那为什么不把它们用来指向等价关系的相应结点呢?同理,也是如此
- ❗ 注意可传递性:指向的边,可通过指向的边传递 [层序遍历,指向的关系已获得],所以在建立匹配关系的优化过程中,实际上不用根据关系向上跳
-
- 此时的AC自动机,本质上接近DFA[确定有穷状态自动机]
- 性质1:当前状态,在输入字符后,可以通过一步操作跳转到下一状态【满足】
- 性质2:当前状态,只代表唯一状态【不满足】
- 还是存在等价关系,只是跳转可一步到位
- 时间复杂度:
Double-Array Trie
双数组字典树,顾名思义,用两个数组代表一棵字典树
引入
- 完全二叉树
- 思维逻辑中的树形结构,实际的存储结构是一段连续的数组空间
- 相比普通二叉树:节省了大量存储边的空间 [记录左/右子孩子的地址]
- 优化思想:记录式 👉 计算式,节省空间
- n个结点的字典树
- 开辟了条边的空间
- 但只使用其中的条边
- 故浪费了条边的空间
- 👉 参考完全二叉树的优点,提出双数组字典树
- 同样通过计算获得子结点的地址,而不用存储边的信息
base数组
存储基准值
- 【帮助父结点找到子结点】
- :第个结点存储的值
- 它的第个子结点的下标等于
- [PS]值是自行设置的,可负,可重复
- 思考:如果只有数组,会有如下场景
-
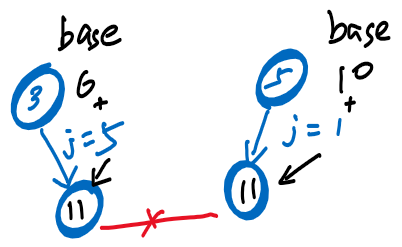
- ❌ 两个结点有编号相同的子结点,即11号结点可能对应多个父结点 [3、5]
- 所以需要确保设置值后,计算的子结点下标不与已使用的下标冲突
check数组
记录父结点的索引
- 【亲子鉴定,检查结点的父结点究竟是谁】
- :第个结点的父结点下标
- 当通过值计算的子结点下标已有爸爸时,可更换值
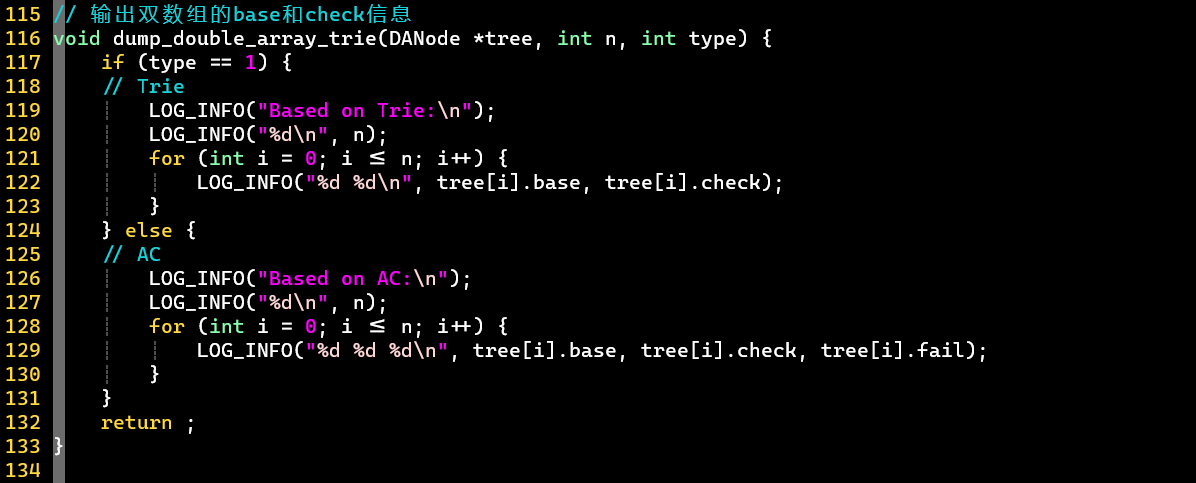
- ❗ 思考:如何记录成词结点
- 值可任意设置
- 而值代表的是下标,一定非负,又可让下标从1开始 [根结点]
- 👉 可用值的正负表示是否成词
- [PS]可代表下标i还没有被使用
公式化
- [PS]
- :第子结点下标,可对应一个字符信息
- :父结点下标
- ,
小结
- 通过两个数组存储字典树的两个重要信息
- ① 父子结点之间的树形结构关系 [+]
- ② 结点是否独立成词 []
- 从而节省了大量边的存储空间
- 一个字典树👉多个双数组,一个双数组👉一颗完整的字典树
- 此时,字典树也只是思维逻辑中的树形结构,实际存储的是两段连续的数组空间
- ❗ 离线存储结构
- 很方便传输、还原
- 但动态插入极其浪费时间
- 实际使用时,一次建立,多次使用 [查询]
+ 二叉字典树
顾名思义,每个结点只有两个分支
- 插入二进制串的字典树,可插入任意信息 [计算机中任何信息都可以看成一个二进制串]
- 极其节省空间,但浪费时间
- 减少了宽度,增加了深度
- 本质:时间换空间
- ⭐ 二叉字典树+哈夫曼编码
- 在节省空间的同时,最大限度节省了查找时间 [减少深度]
代码演示
Trie
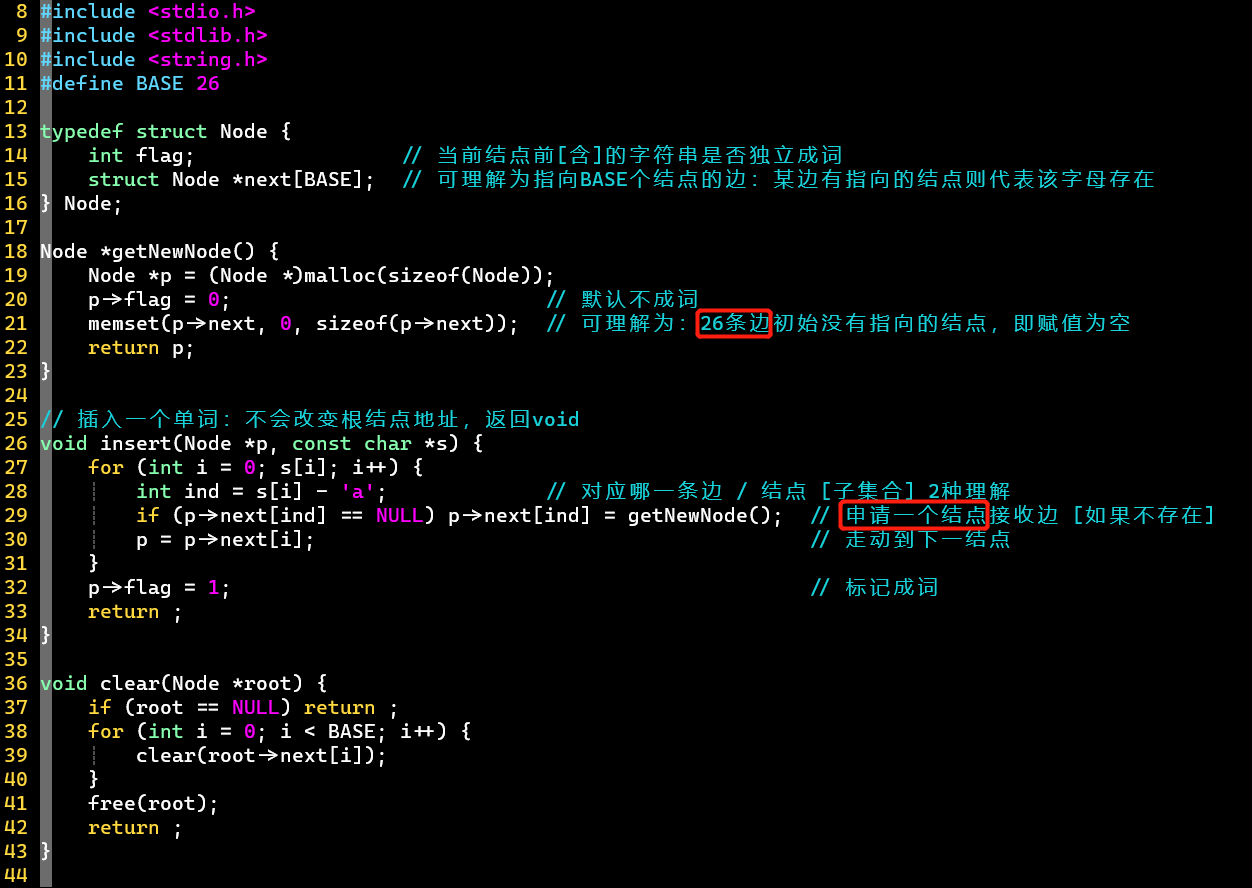
- 上为字典树的标准数据结构式的代码实现,用于刷题的技巧性实现方式见下 [HZOJ-282]
- 结构定义
- 对于26个字母,结点中对应存储26个结点,可理解为代表字母信息的26条边
- 通过,标记成词结点
- 结构操作
- 插入单词不会改变根结点地址,所以函数返回值为void
- 存在指向某索引的结点,就代表存在对应的字母信息
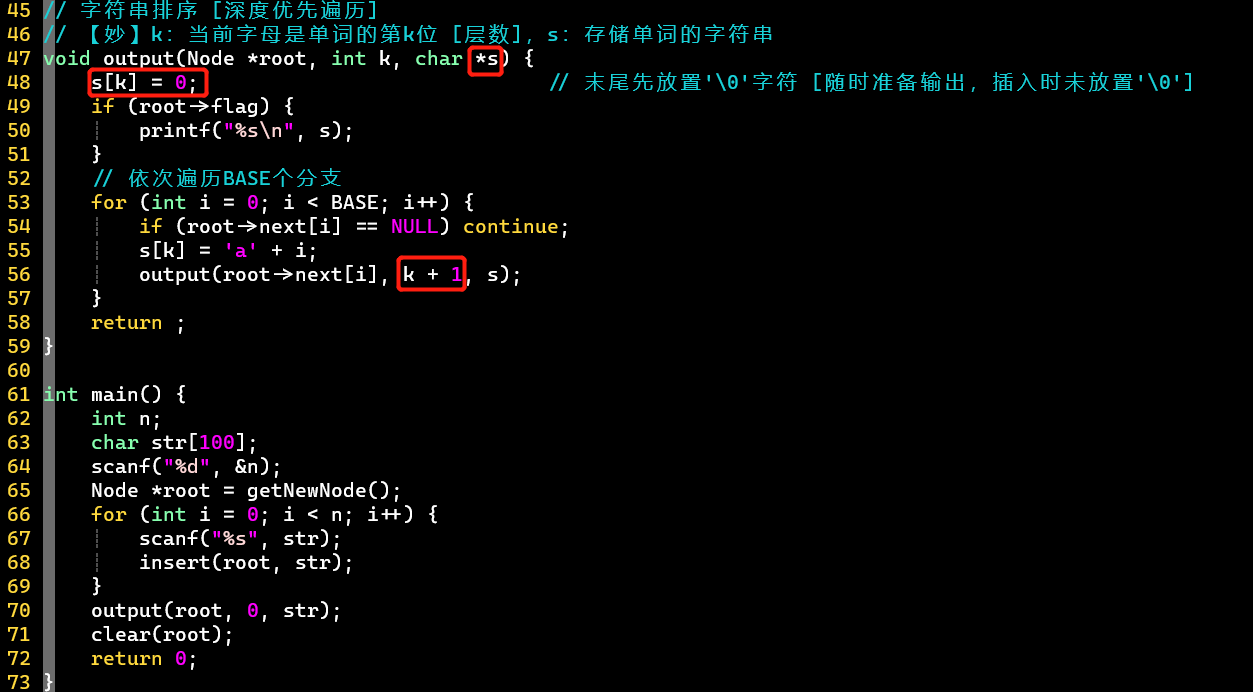
- ⭐字符串排序
- 通过指示当前所在层数,存储字符串信息,通过每次在末尾置0,随时准备输出字符串
- 利用递归的方式进行深度优先遍历,关键在于理解
AC自动机
普通版
数组未充分利用
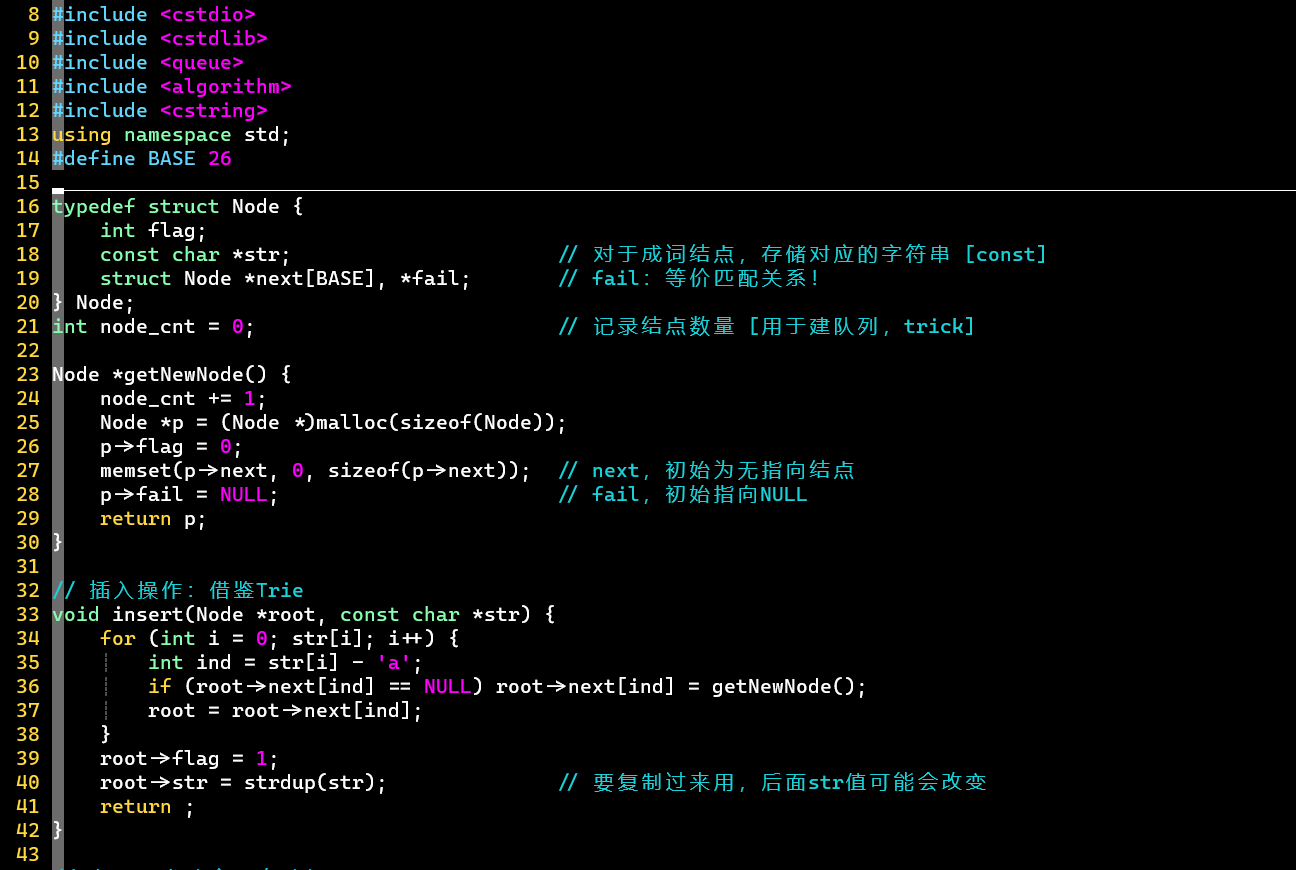
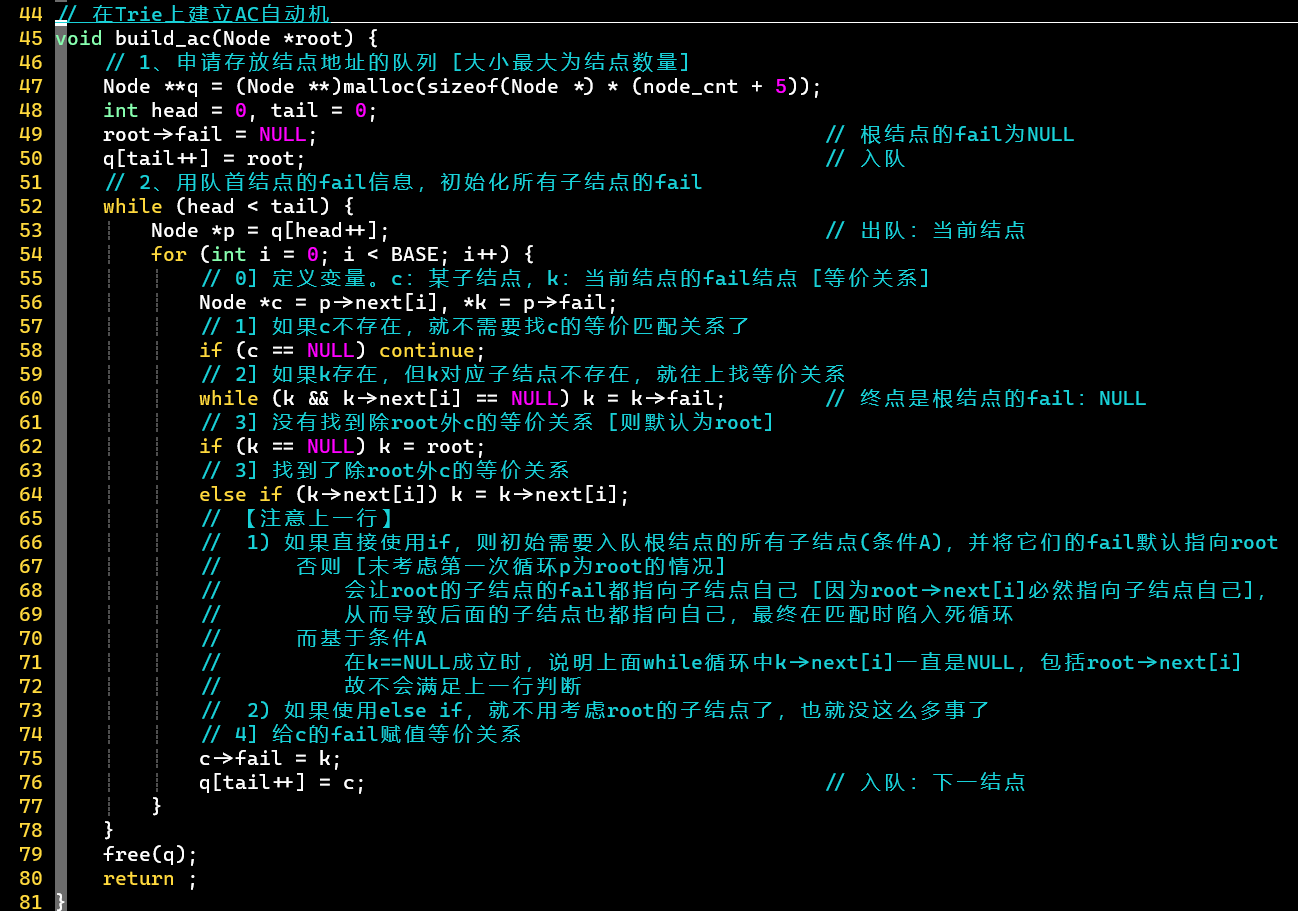
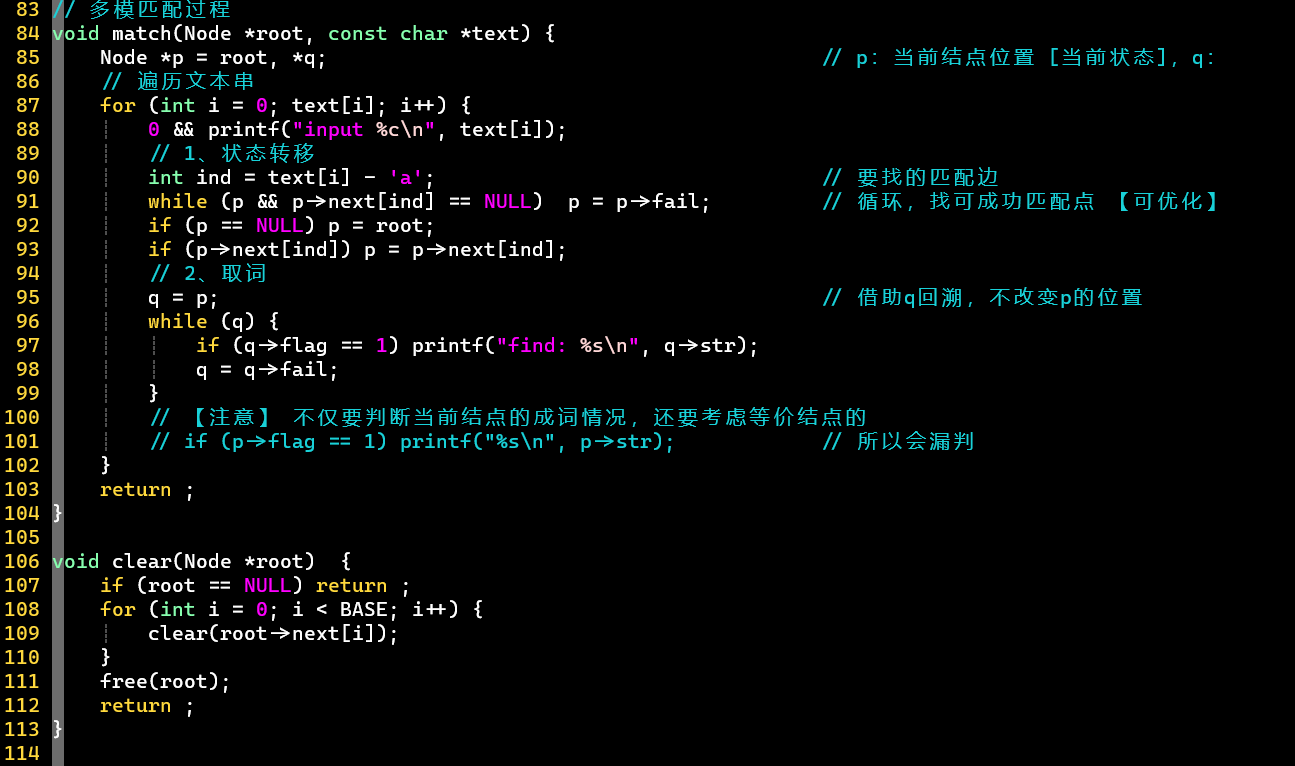

- 建立Trie树 👉 建立等价匹配关系 [队列、] 👉 匹配 [状态转移、取词]
- 注意
- 根据等价关系向上跳的操作,不仅发生在建立和使用匹配过程中,还发生在取词过程中
- 建立和使用等价匹配关系的while循环,耗时很大,可优化
- [思考:建立等价关系过程] 根结点的子结点的等价匹配关系必然指向根结点
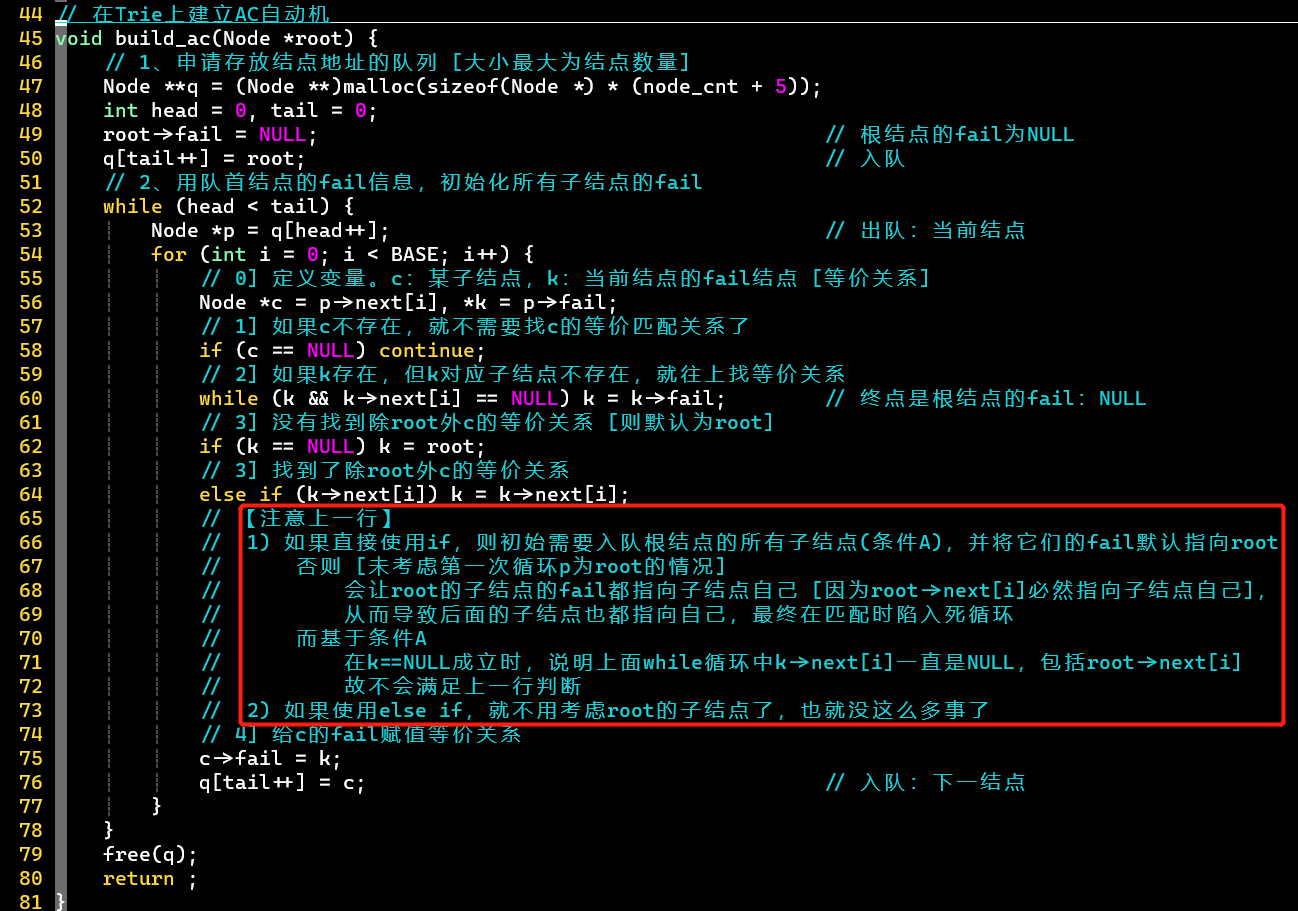
- 第64行若使用if,则需考虑第一次循环为root的情况
- 为root的子结点,直接为NULL,在第60行会直接跳出while循环,在第62行k赋值为root,但第64行若用if,root->next[i]必然成立,因为就是root的子结点自身
- 在这里,可以将根结点的子结点统一考虑,但在优化版中还是需要单独拿出来做处理
优化版
充分利用数组,建立和匹配过程都得到了优化
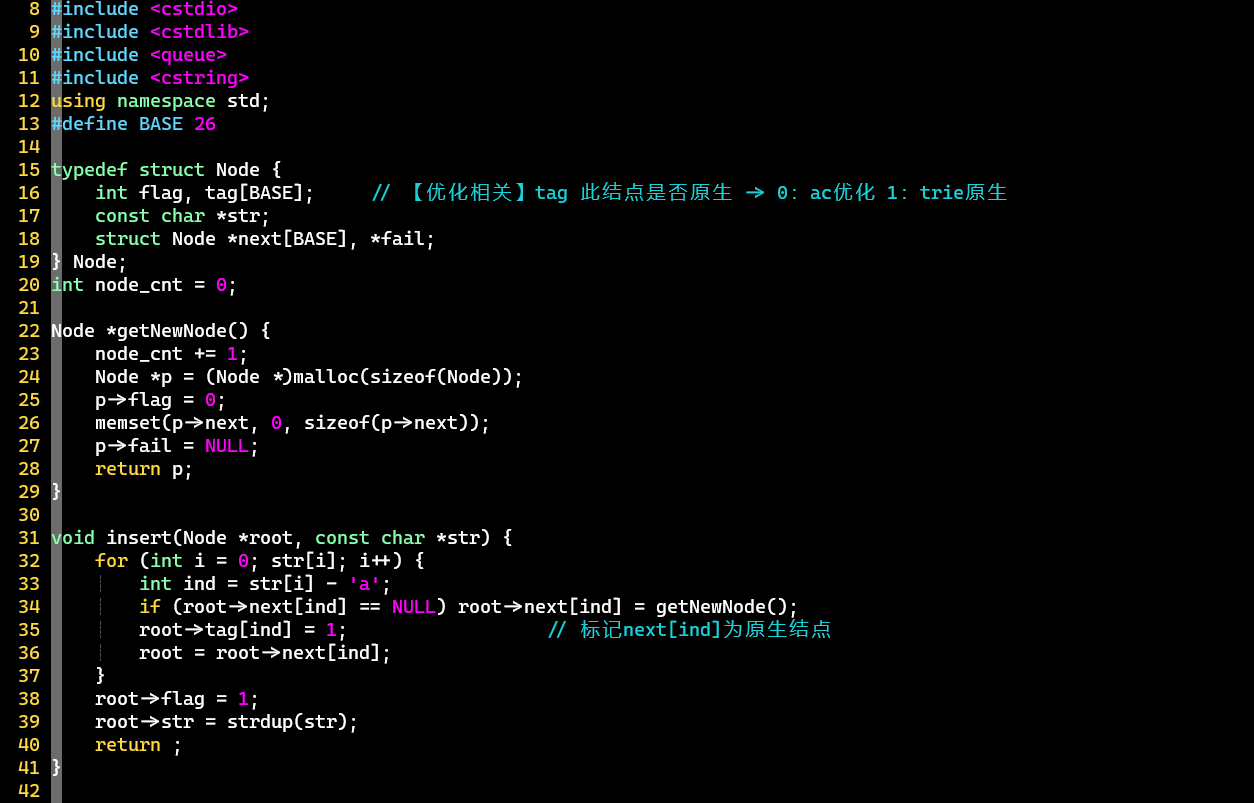
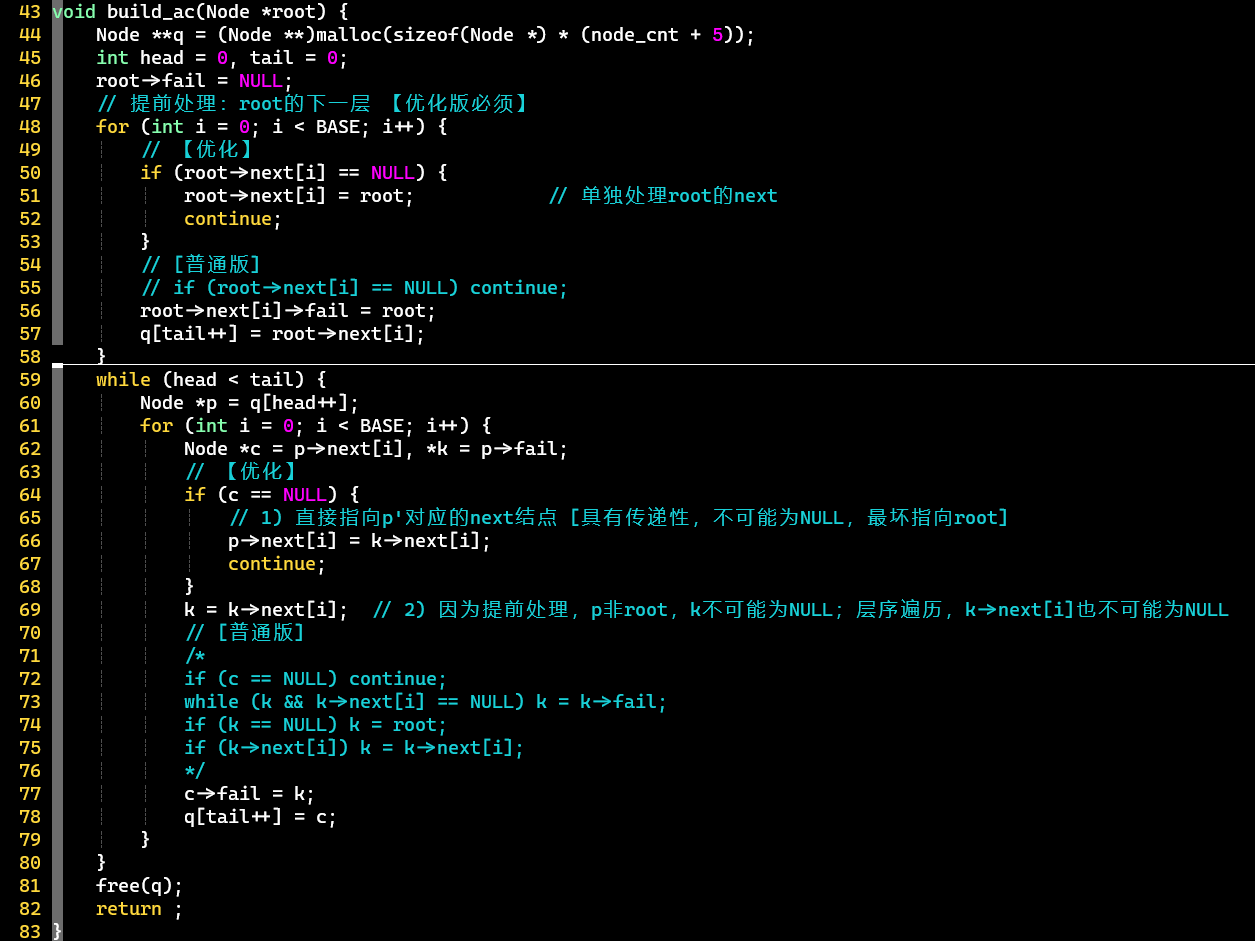
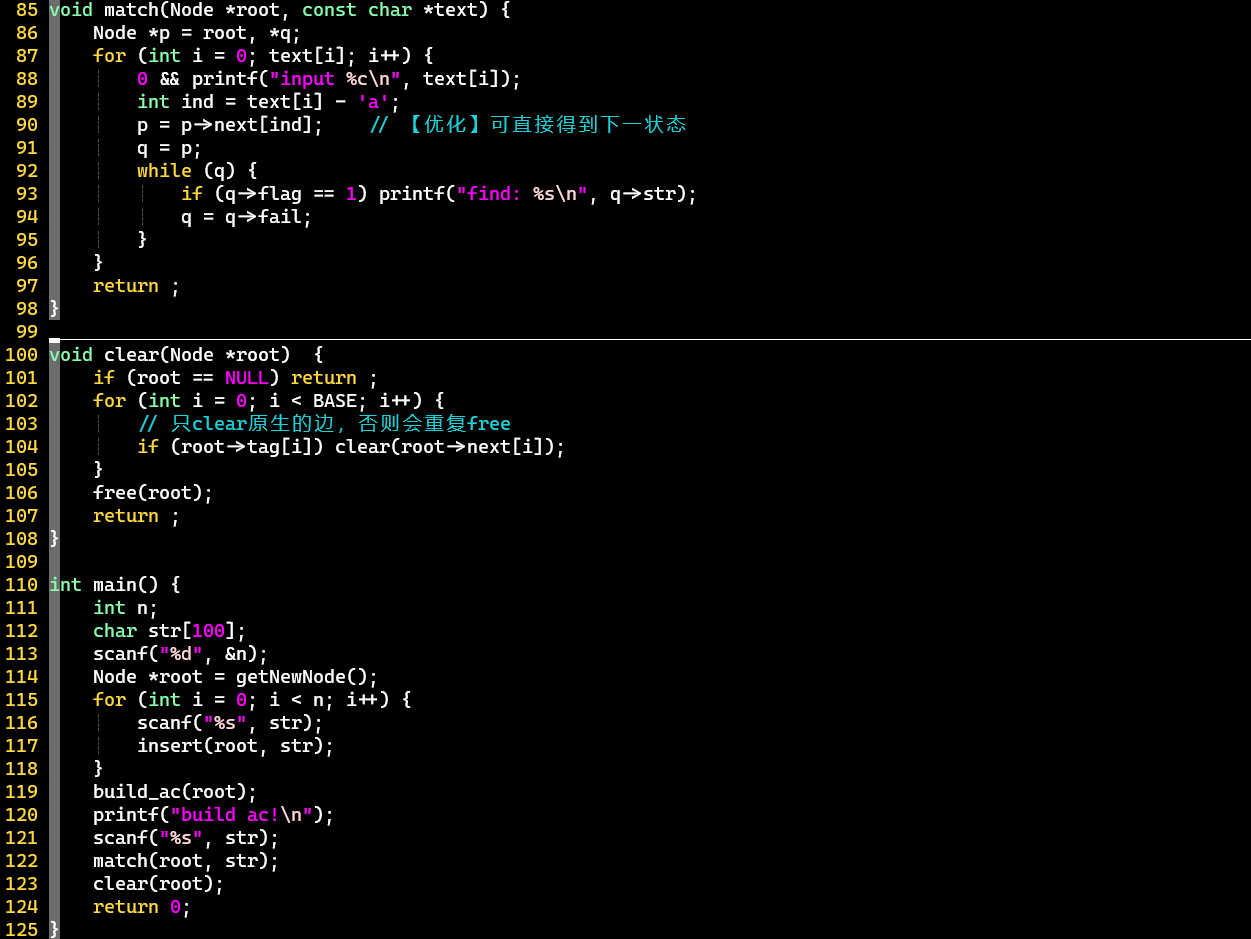
- 优化:在当前结点的为空时,直接将其赋值为等价关系的[①];否则,将当前结点的的等价关系指向①
- 注意:根结点需要特殊处理,两种情况都赋值为root自身 [②]
- [PS]
- 只有root的指向NULL
- 销毁时需要判断:结点是否为字典树原生,否则重复free可能引发错误
- AC优化使用的结点对应了原生结点
DAT [+AC自动机]
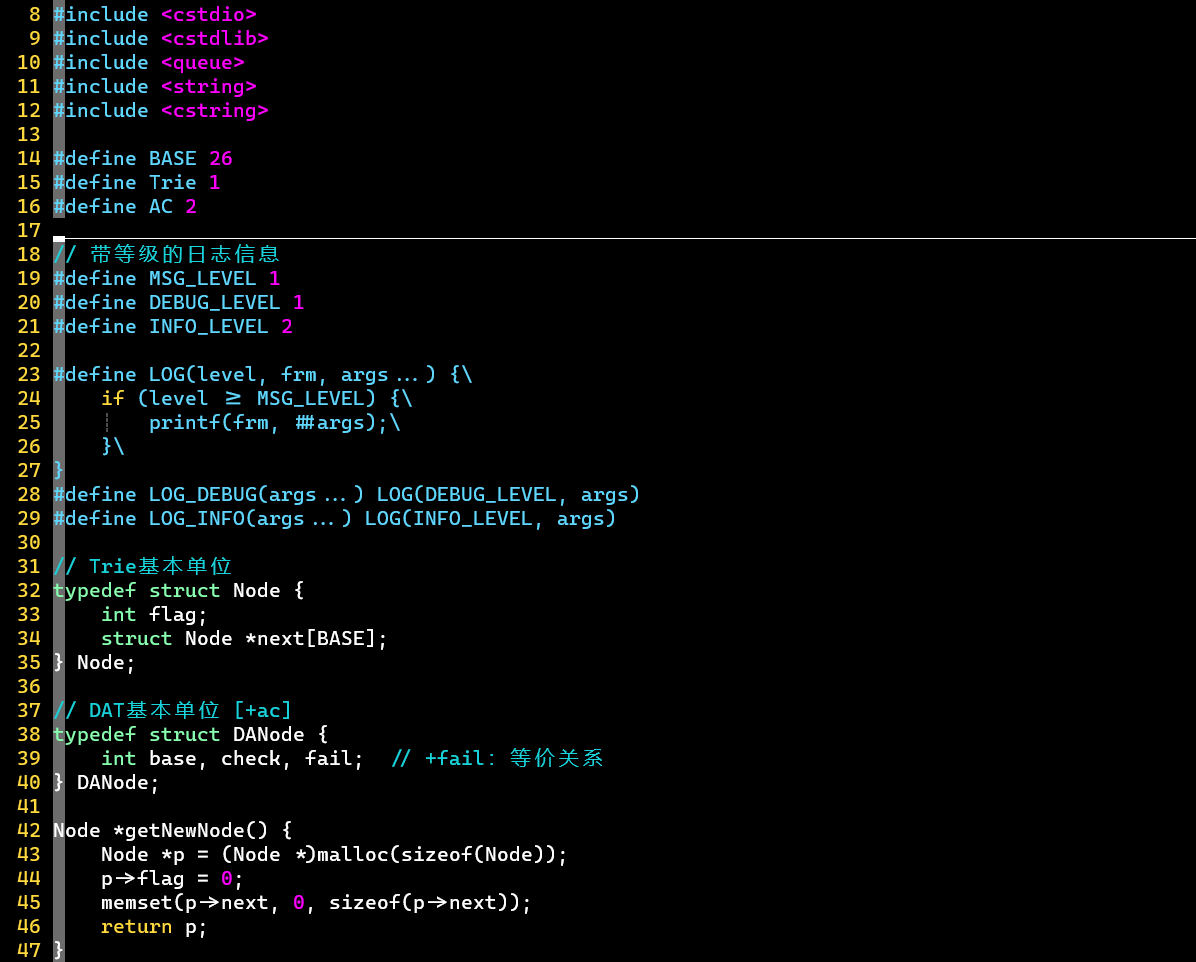
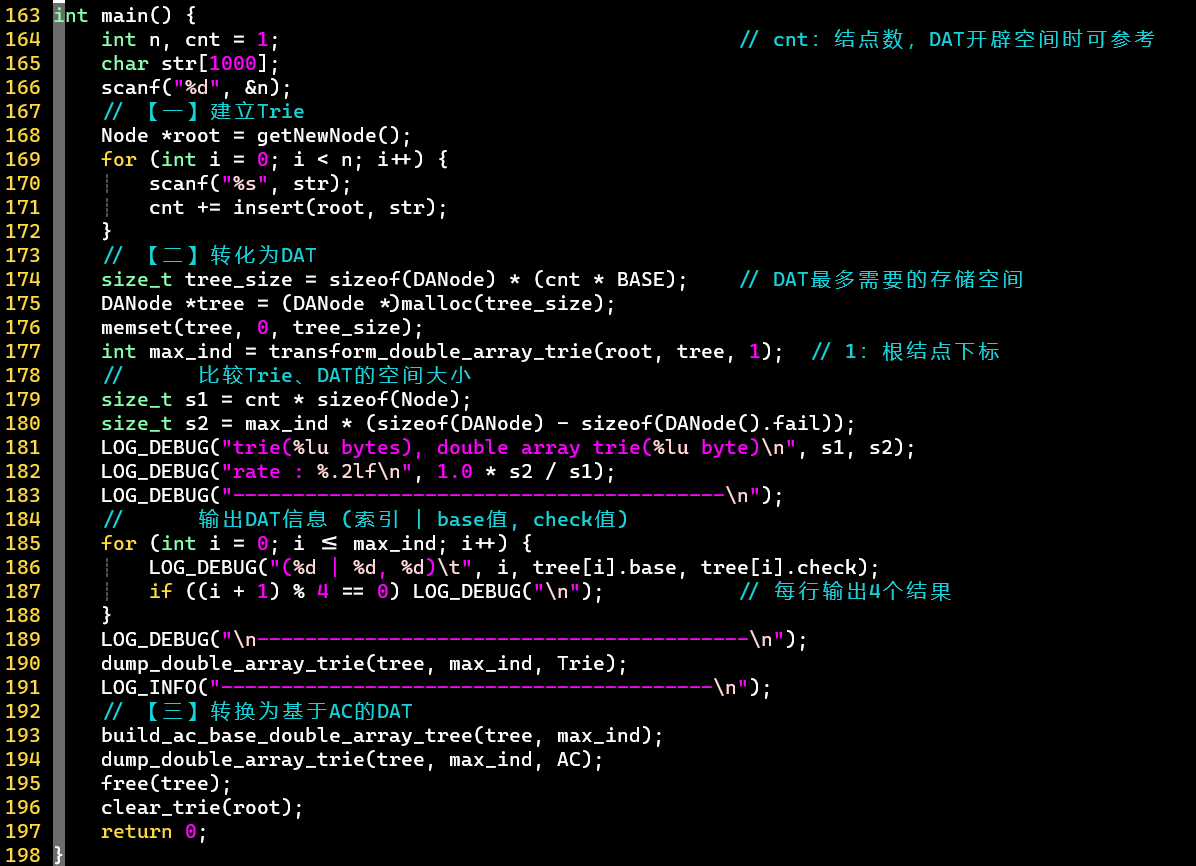
- 【一】先根据输入的单词们,建立Trie
- 为了方便,基于Trie来实现DAT
- :记录字典树的结点数
- 使用了内联函数,参考C中关键字 inline 用法解析——CSDN
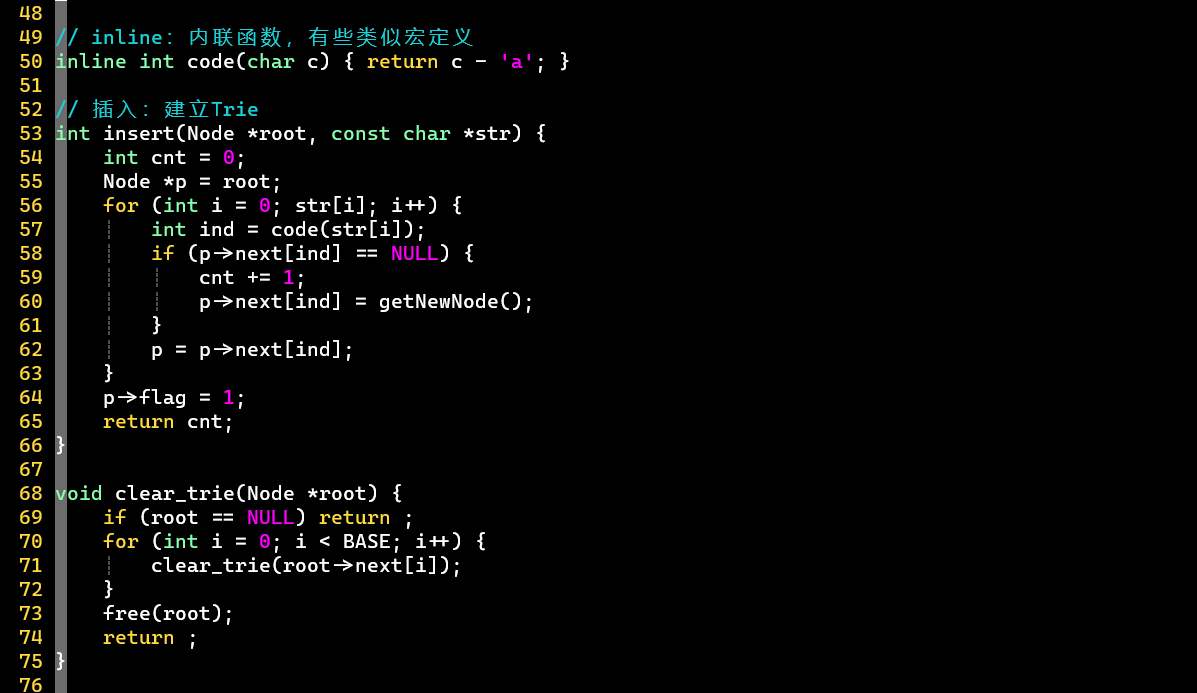
- 【二】将Trie转换为DAT
- 0] 若该结点成词,更新为负
- 1] 依次标记子结点的
- 2] 依次标记子结点的
- [PS]
- 记录最大下标
- 结点下标从1开始,值从1开始
- 值的确定方式有很多,这里采用的暴力方式
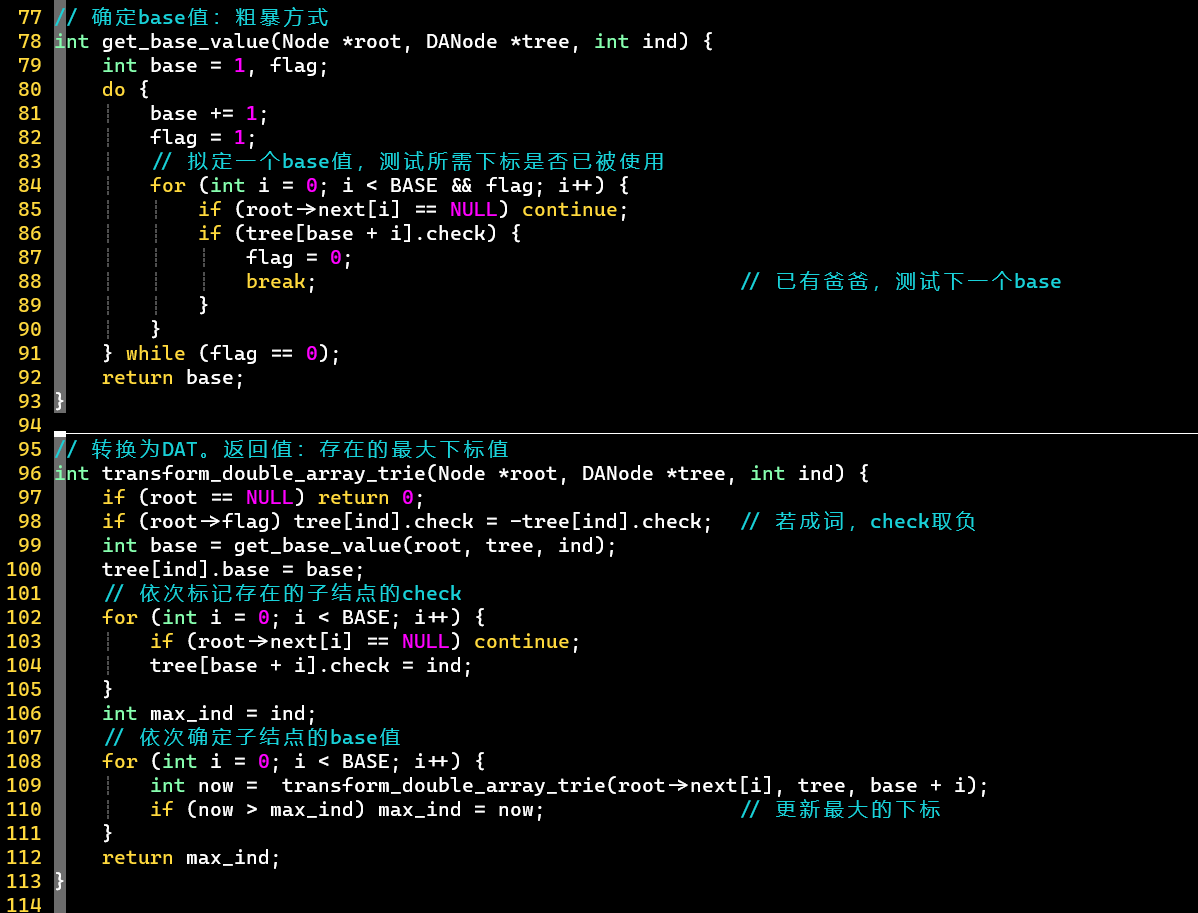
- ⭐ 通过下列信息(),即可转换出字典树信息
-
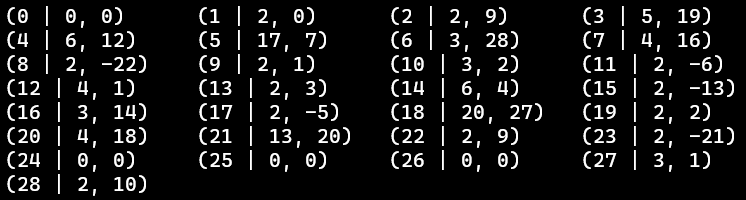
- 转换步骤
-
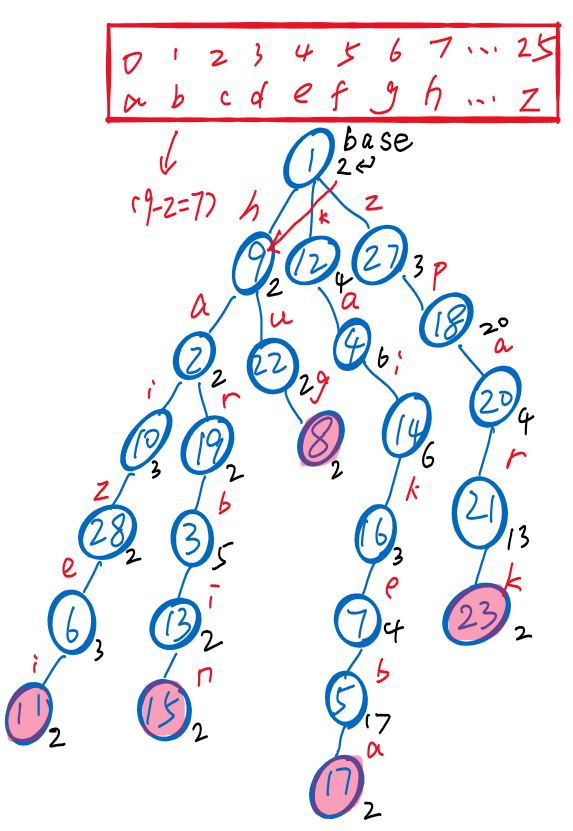
- ① 先画出根结点,找的三元组对应下标,即根结点的子结点下标
- ② 再依次找出子结点的子结点们的下标,进而画出整棵字典树的结构
- ③ 最后,根据父结点的值和子结点的编号之差,得到边对应的字符信息
- [PS]值为负→成词
-
- 👉 双数组非常方便输出到文件中,再进行机器之间的共享,即共享DAT
-
- 比较上面字典树信息对应的Trie和DAT实际空间大小
-

- DAT的压缩效率约25倍❗
- 可尝试利用真实数据集,测试DAT的压缩效率
-
- [PS] 实现了带等级的日志信息系统
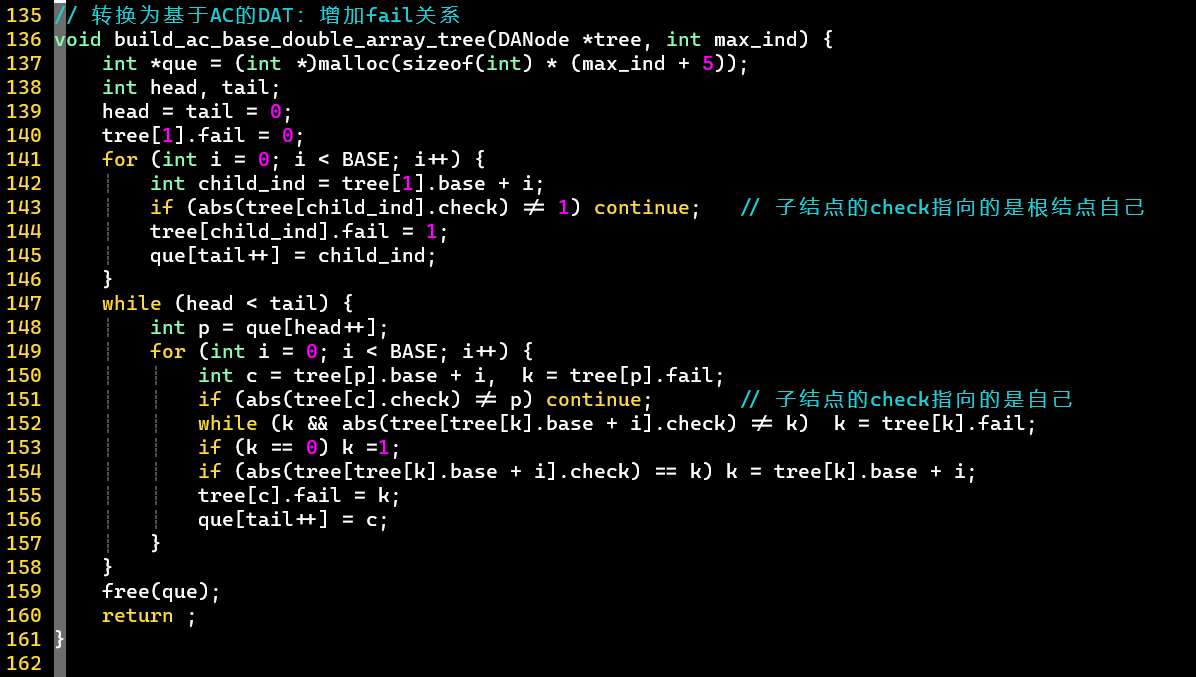
- 【三】增加指针,将DAT转换为基于AC自动机的DAT
- 逻辑不变,代码实现上注意
- 该结点有第个子结点 👉 该子结点编号对应的值指向自己的编号
- 无需使用路径压缩,本身就没有可利用的“废物”
- 逻辑不变,代码实现上注意
随堂练习
HZOJ-282:最大异或对 [Trie]
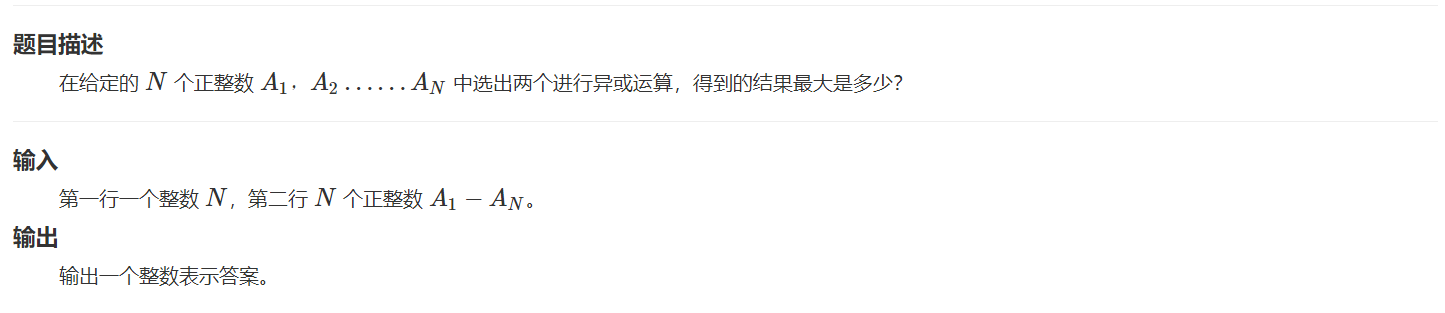
样例输入
3
1 2 3
样例输出
3
- 思路
- 【思考】如何使异或结果尽可能大
- 参与异或运算的两个数字,二进制表示的每一位尽可能不同
- 【问题转换】
- 确定一个数字
- 找从高位到低位尽可能不同的另外一个数字 [位置越高权重越大]
- 即找到最大异或对
- 【实现步骤】使用字典树
- ① 把每个数字看成一个二进制串,插入到字典树中
- ② 采用贪心的策略,遍历每个数字,找其对应异或值最大的另一个数字
- ③ 最终得到最大的异或值
- 【思考】如何使异或结果尽可能大
- 代码
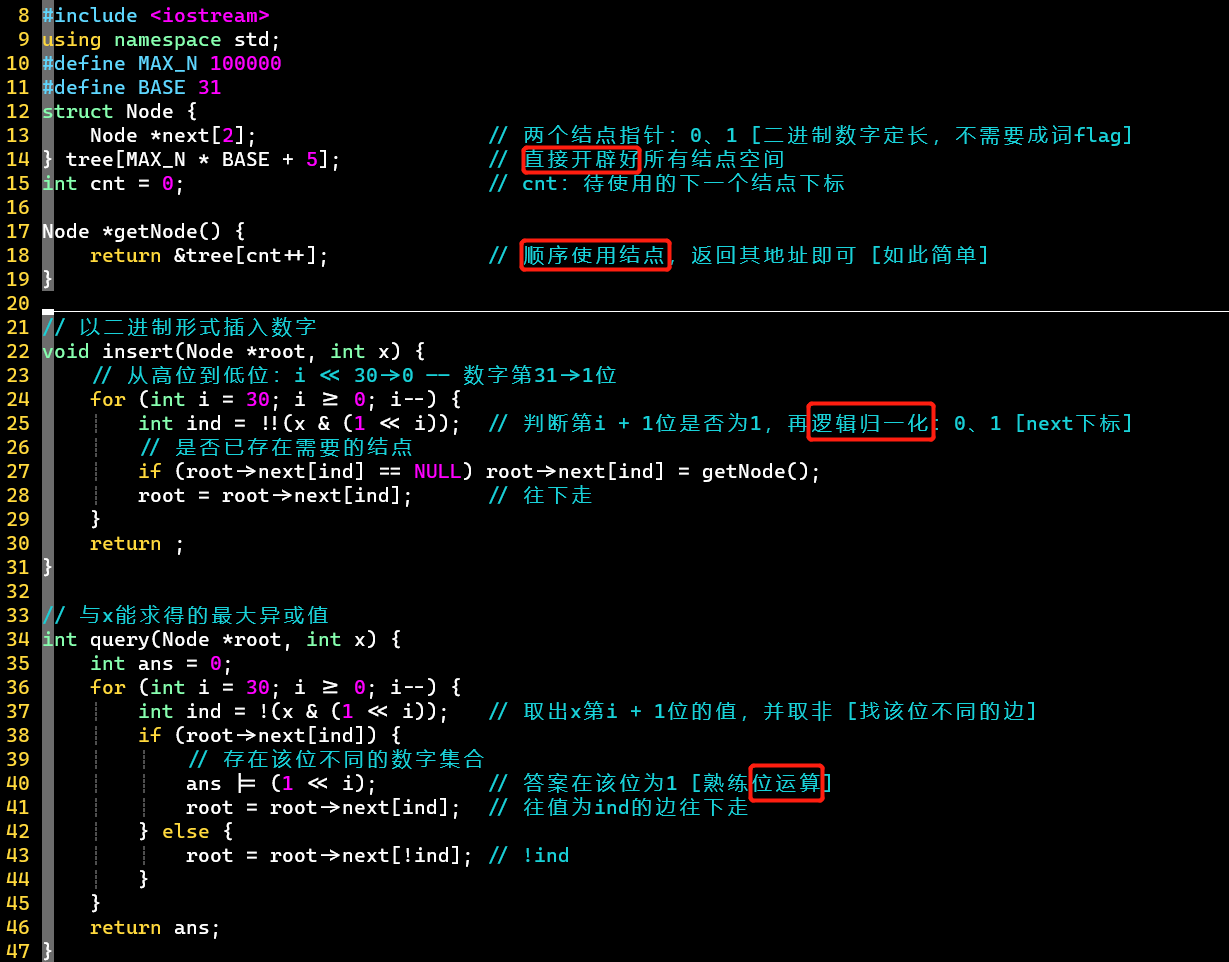

- ⭐亮点很多:直接开辟所有结点空间、顺序使用结点空间;擅用位运算;贪心遍历,边查询边插入
- 结构定义
- 根据题意,最多需要个结点,直接开辟好
- 有符号int型的有效位为定长位,所以不需要成词的
- 结构操作
- 从高位到低位插入数字的每一位
- 利用逻辑归一化将有效位转换为1,作数组的下标用 [只有0、1]
- 贪心遍历
- 查询时不需要和自己异或,所以查询完再插入到字典树
- 当某一位可以异或得1,擅用位或运算加到答案里
伴随编程:字符串统计 [AC]
【预习】数据结构(C++版)

样例输入
2
ab
bca
abcabc
样例输出
0: 2
1: 1
- 思路
- 多模匹配问题 [AC自动机裸题]
- 关键
- ① 使用解题套路版代码实现:直接开辟大数组
- ② 维护每一个单词的计数量:使用幼儿园必知必会的指针技巧
- 注意:输入数据中给的模式串中有可能重复
- 代码
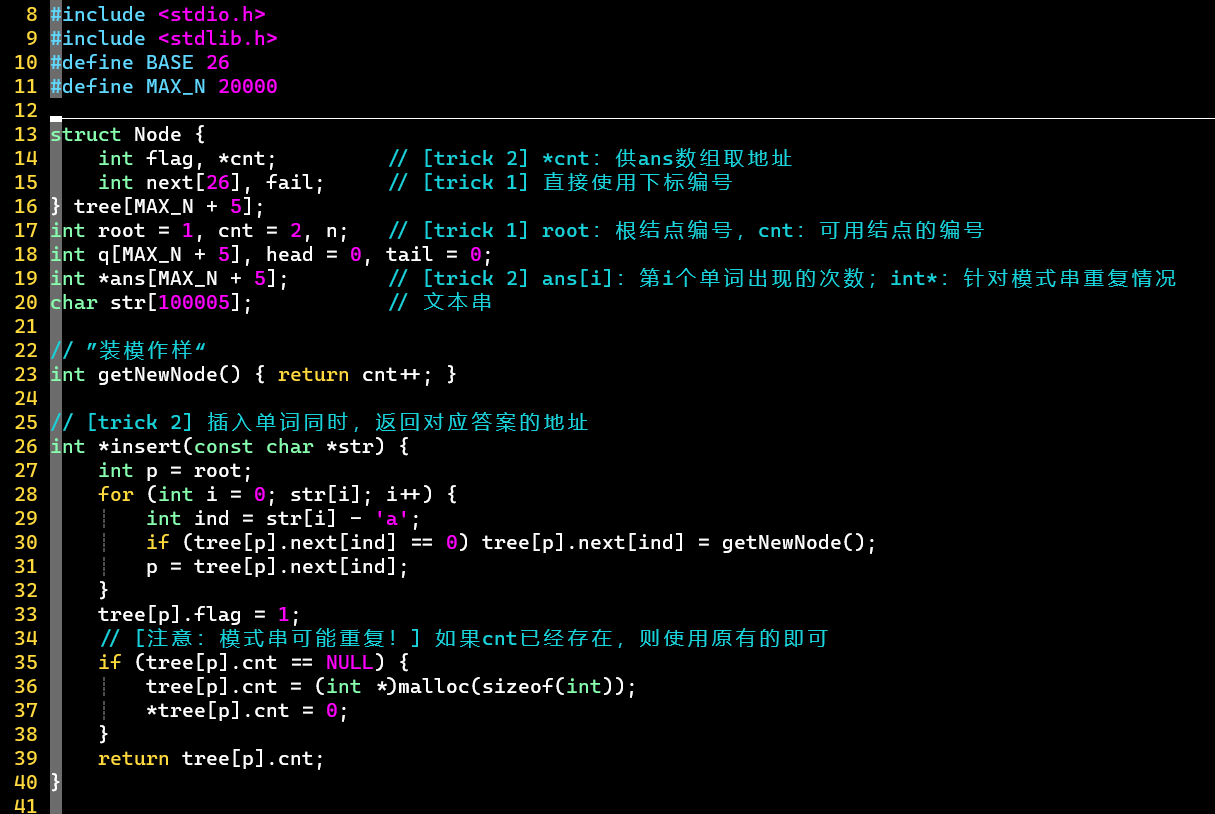
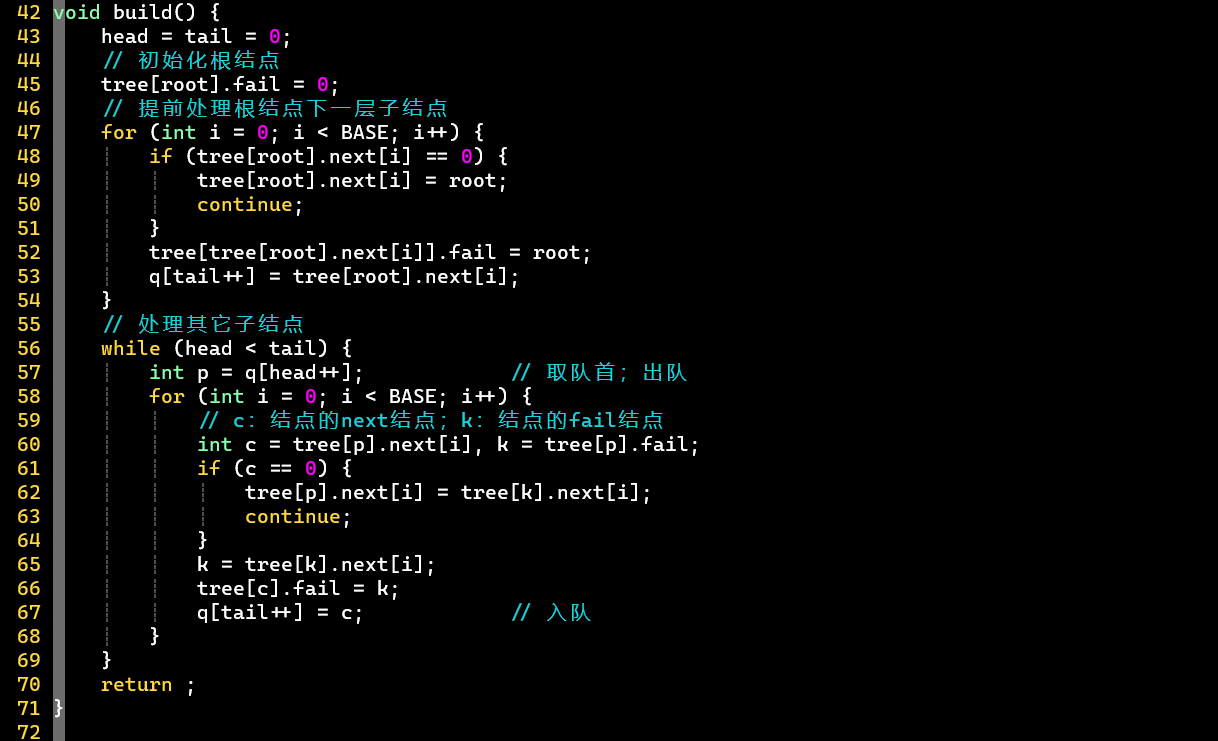
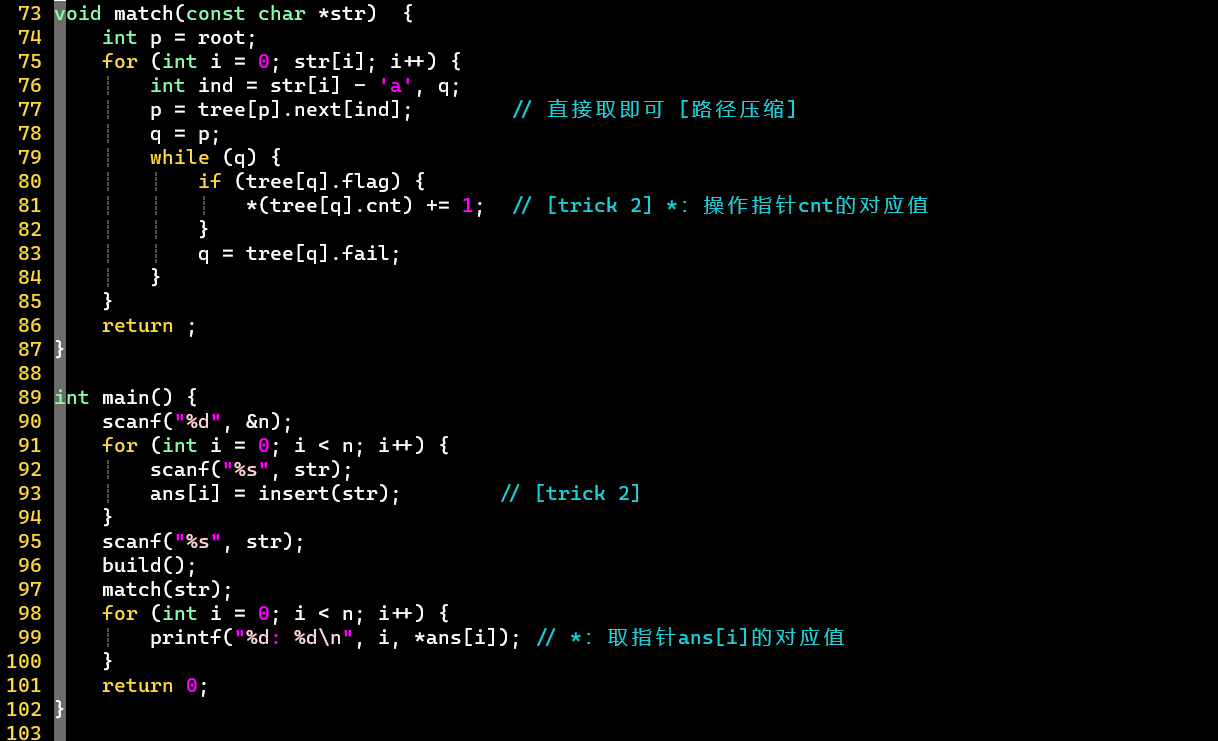
- [考验代码功底]
- 2 tricks ⭐
- ① 开辟大数组,用下标代表结点
- 数组大小 [结点数量]:最多
- 空结点用0表示,记录下一可用结点编号
- 使用下标时,注意代码实现思维的转换
- ② 利用指针绑定模式串与答案,并固定答案的顺序,可实时更新
- 针对模式串重复可能,数组也使用int*类型,相同模式串的答案可指向同一地址
- 匹配时,操作指针地址上的值即可
- ① 开辟大数组,用下标代表结点
附加知识点
- 字典树的本质:字典数据的另外一种表现形式,等价于一本字典
- AC自动机的本质:状态机
- 在实际应用中,AC自动机不如字典树暴力匹配广泛 [在开发效率和执行效率中的平衡]
- DFA、NFA是编译原理的知识
- 主要区别:DFA速度更快,NFA消耗内存更少
- 参考Difference between DFA and NFA——Stechies
Tips
- 建议:多看几本基本的算法书、数论基础书,多接触离散型数学思维
- 错误式学习:学习什么是错的,减少错误的概率
- 得道者多助,失道者寡助;万物都有成熟的时令;不积硅步,无以至千里;不积小流,无以成江海
- 寄语:以吾之矛,武装汝身


