计算机中的树与现实中的形态相反,是一棵倒挂的树~
课程内容
树
- 树的组成:结点 + 边
- 结点 👉 集合,边 👉 关系
- 根结点:全集;子结点:子集
- 根结点的所有子结点的集合并集 = 全集
- 【思想】大问题抽象为树,小问题抽象为子结点
结构定义
【结点 + 边】
-

-
一叉树是链表结构,只有一个分支的树形结构
-
对于三叉树,则将链表的next指针变成next[3]数组即可
属性、性质
-

-
深度、高度
- 树的深度和高度是一个值:最大层数
- 结点的深度和高度不一样
- 深度:从根结点往下数,该结点是第几层
- 高度:从最深的层数往上数,该结点是第几层
-
度:有几个子孩子
-
⭐【重要公式】结点数 = 边数 + 1
二叉树
- 二进制可以转换成任何进制,二叉树同理
- 首先简单
- 且可以表示所有的树形结构
- 方法:左孩子、右兄弟法,又称十字链表法
-

- 从上往下,从左往右,结点的孩子放在左边,结点的相邻兄弟放在右边
- 对于n叉树,n不确定,而二叉树是确定的
- n叉树可以用二叉树来实现
- 所以,利用二叉树可以将非确定性问题 → 计算机能解决的确定性问题
- ⭐【重要公式】二叉树中,度为0的结点比度为2的结点多1个
- 利用另一重要公式:结点数 = 边数 + 1
- 令ni表示度为i的结点个数
- 则:[结点数] n0 + n1 + n2 = n1 + 2 * n2 + 1 [边数 + 1]
- 得:n0 = n2 + 1
- 遍历方式:取决于什么时候[最先、中间、最后]访问根节点
- 前序遍历:根 左 右
- 中序遍历:左 根 右
- 后序遍历:左 右 根
- 遍历时的左、右可以分别代表左、右子树
- 左右的相对顺序一直是左在前,右在后
- 二叉树分类【国际版】,参考Binary tree: Types of binary trees-维基百科
-

- 完全二叉树:除了最后一层最右边可以缺少若干连续结点,其他地方都满满当当
- 满二叉树:度为0或2即可
- 完美二叉树:度均为2,所有叶结点在同一层
- PS:中国版只分完全二叉树和满二叉树,满二叉树的定义同国际版的完美二叉树
-
- 完全二叉树的特点 [完美二叉树同样满足]
- 编号为 i 的结点的左右孩子编号分别是2 * i、2 * i + 1
- 可以用连续空间(数组)存储,用于算法优化:记录式👉计算式
- 不再需要用结构体存储孩子结点的地址,直接通过公式可计算其在数组中的索引
- 广义表:树的字符串化
-
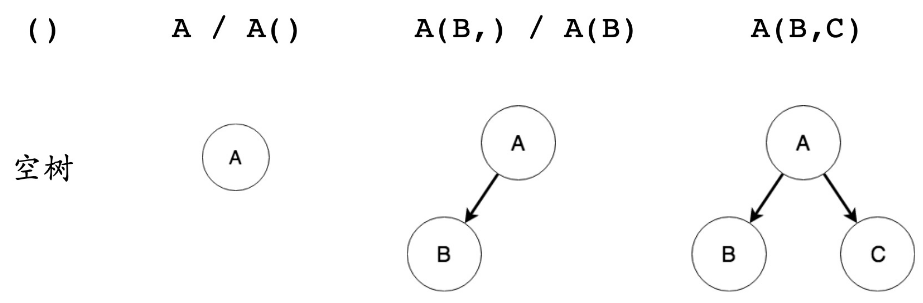
-
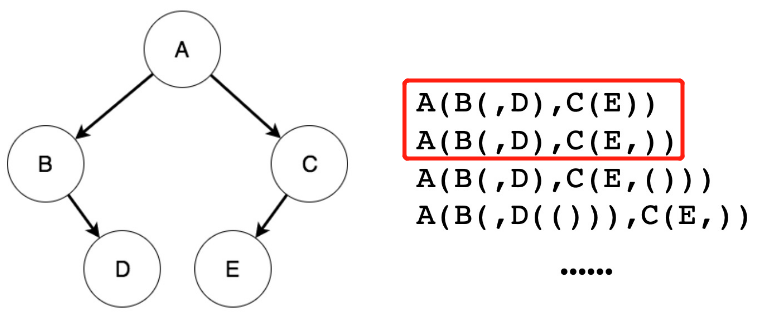
- 有很多种表示方法,一般怎么简单怎么来,见上图红框:方式一、方式二
-
- 对于二叉搜索树,中序遍历是顺序的
- 根据两种遍历可得第三种遍历结果
- 前序遍历/后序遍历可得根结点,中序遍历可得左右孩子的位置
- 【必须】要有中序遍历,只有它才能确定孩子的左右
代码演示
二叉搜索树
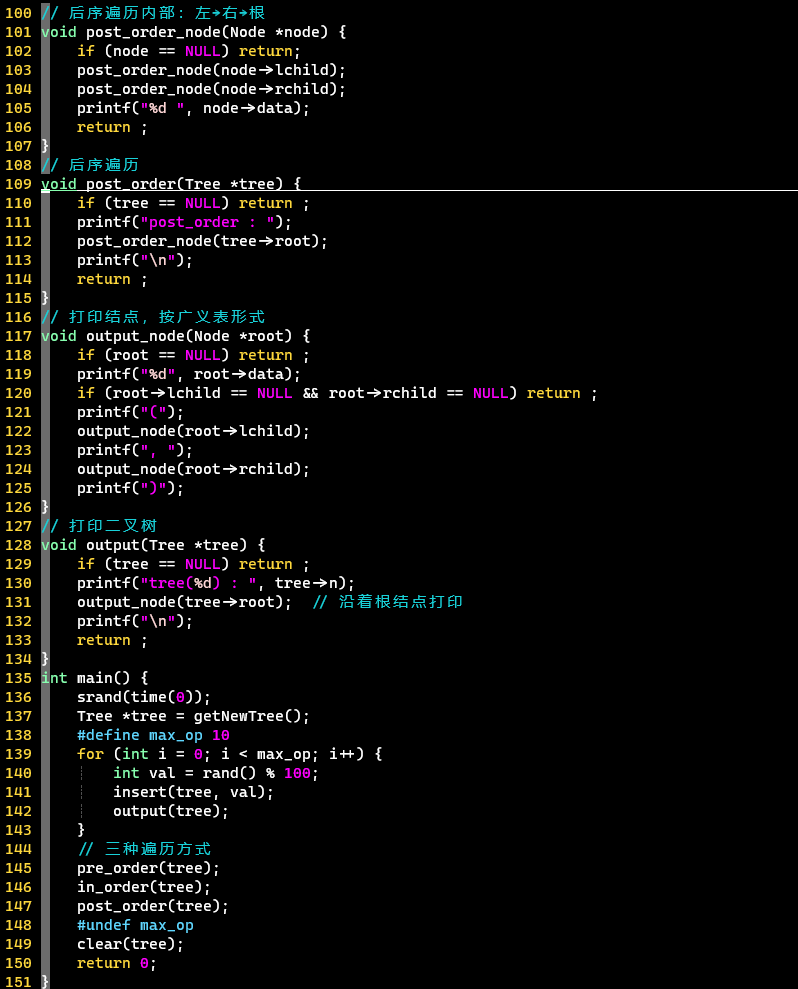
结构定义、结构操作、遍历结果显示
-
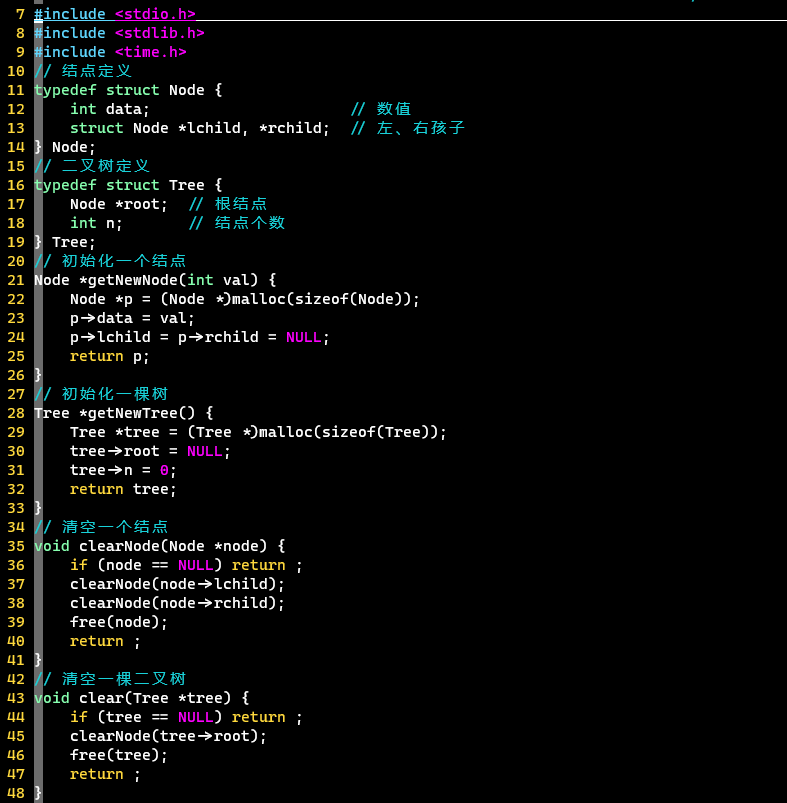
-
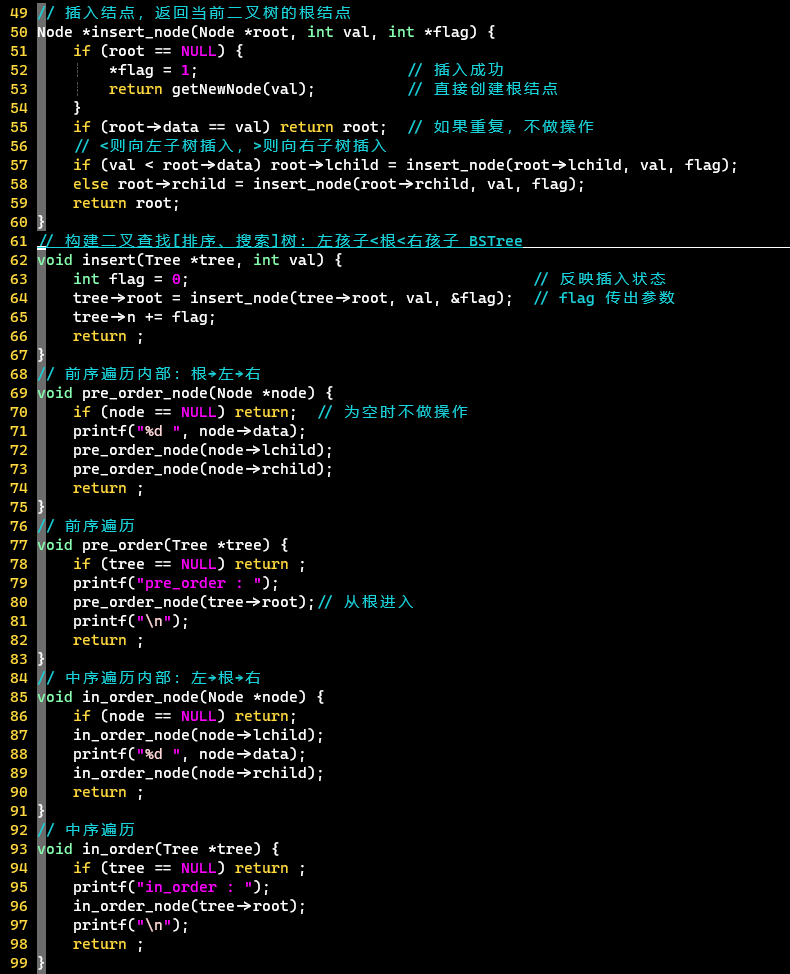
-
-
树和结点的操作是分开实现的,独立封装
-
插入操作
- 使用flag获取插入状态
- 二叉搜索树没有重复值
-
遍历操作
- 三种遍历的内部实现,就调换一下访问左右根的顺序即可
- 二叉搜索树的中序遍历是有序的,从小到大排序
-
输出:广义表形式为前述第二种方式
-
❓结构体里的结点都定义为指针形式,自己的理解是
- 结点是一个结构体,用指针存储地址更省空间
- 结构体指针调用成员更方便:->
- 方便free结点
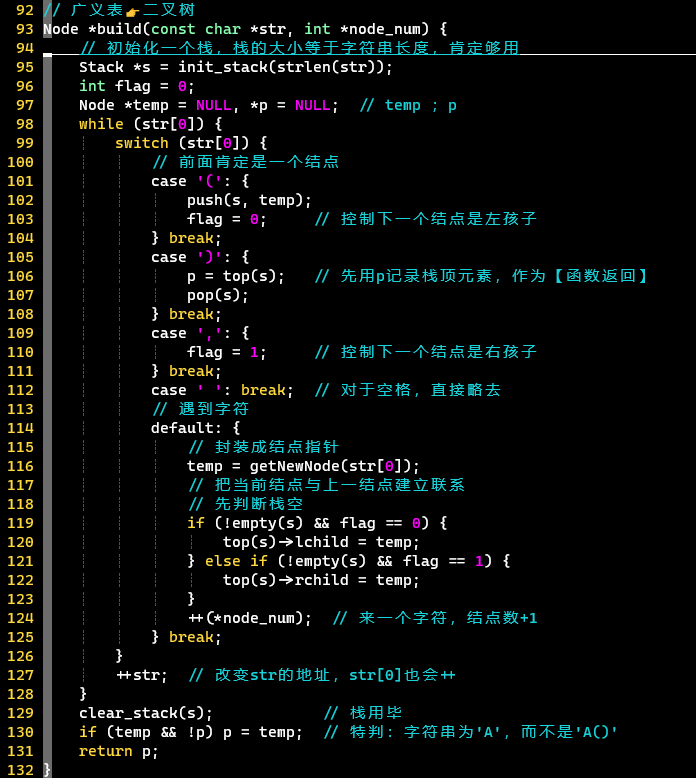
广义表还原二叉树
-
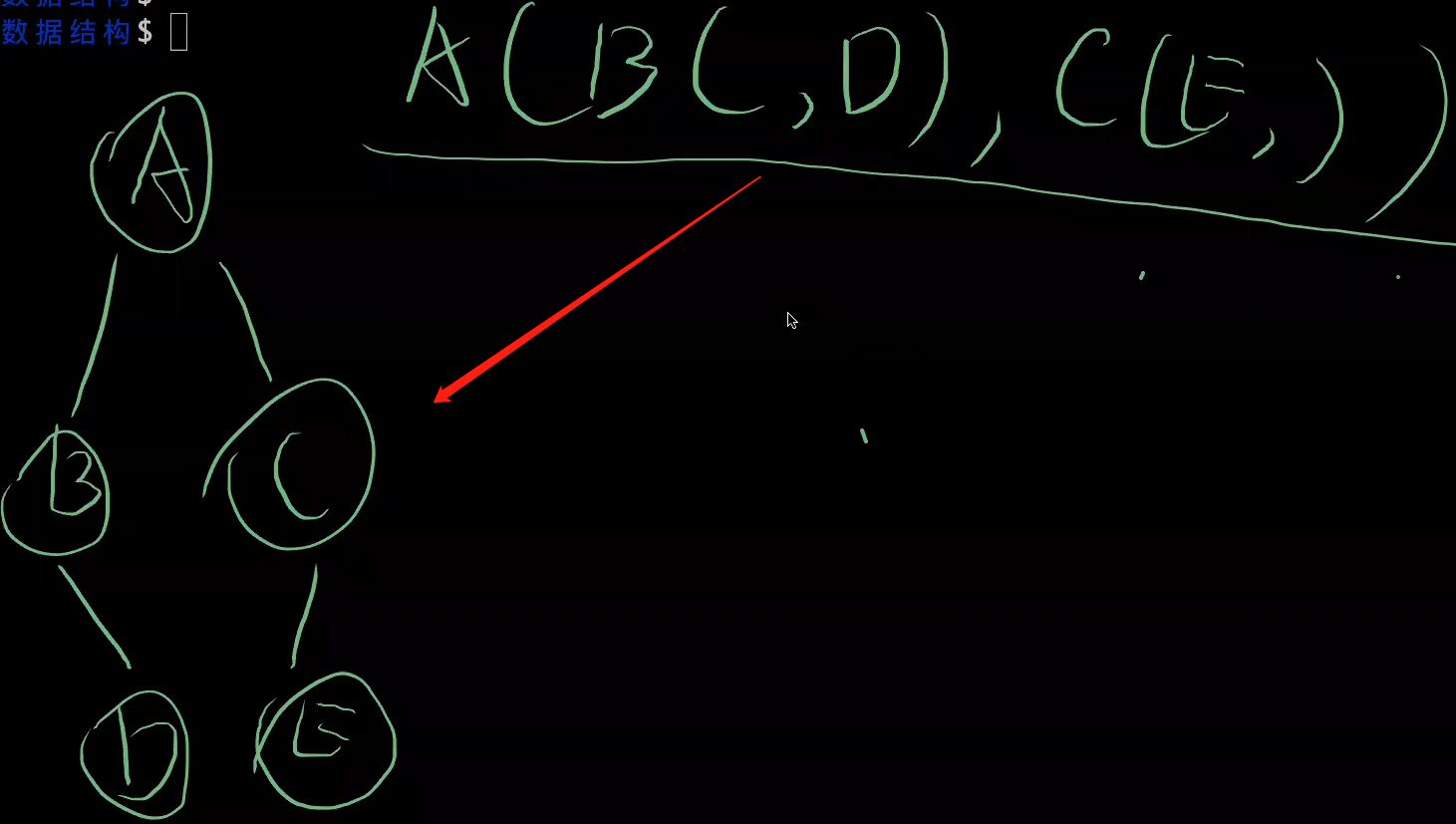
-
具有完全包含关系的问题,使用栈
-
栈里存储结点地址[Node *]:把广义表中的字符看成结点
-
转换过程
|(|,|)|其他字符【字母】|
|:----😐:----😐:----😐:----😐
|【将元素入栈】
下一个','前的元素为左孩子|决定下一个字符封装的元素为【右孩子】|记录栈顶,【将元素弹栈】|①将字符【封装】成结点指针类型,作为栈的元素
②【关系确定】如果栈不为空,则根据该字符相对于','的位置,成为栈顶元素的左孩子或右孩子|
代码
-
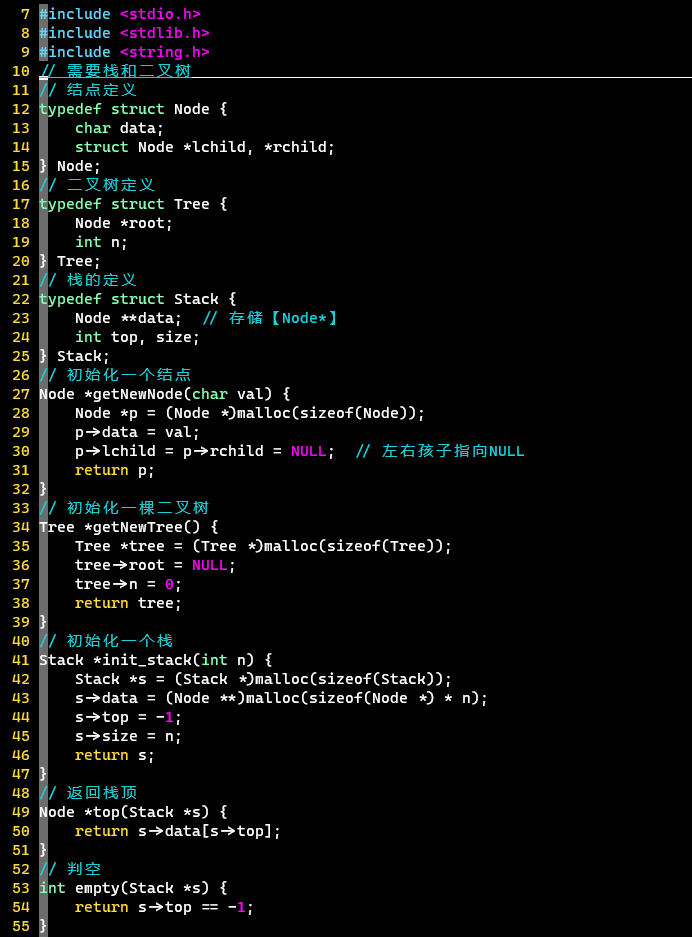
-
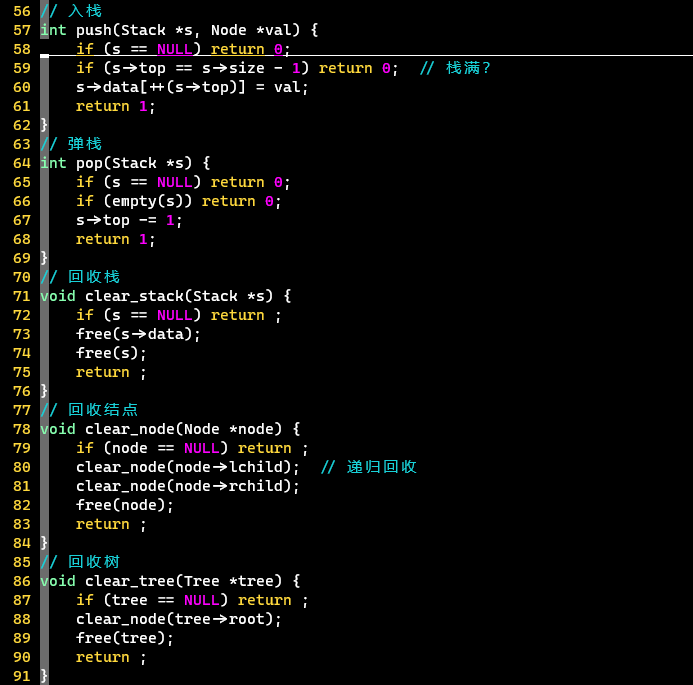
-
-

-

-
结构定义、操作定义:栈、二叉树
-
【关键】转换的匹配规则
Tips
- 节点和结点的区别
- 节点是一个实体,它具有处理的能力
- 结点是一个交叉点、一个标记
- 算法中的点一般都称为结点,数据集合中的每一个数据元素都用中间标有元素值的方框来表示,我们称它为结点
- 参考节点和结点有什么区别-php中文网
- 在工业界,除了红黑树,其他树都是玩具级的树形结构
-




