课程内容
回顾[完全二叉树]
-

-
完全二叉树默认从1开始编号
- 这样可以保证左孩子、右孩子编号简洁
- [否则] 左孩子编号需为2 * i + 1,右孩子编号需为2 * i + 2
-
可编号的性质→可用顺序结构存储,而不需要保存下一个结点的地址
-
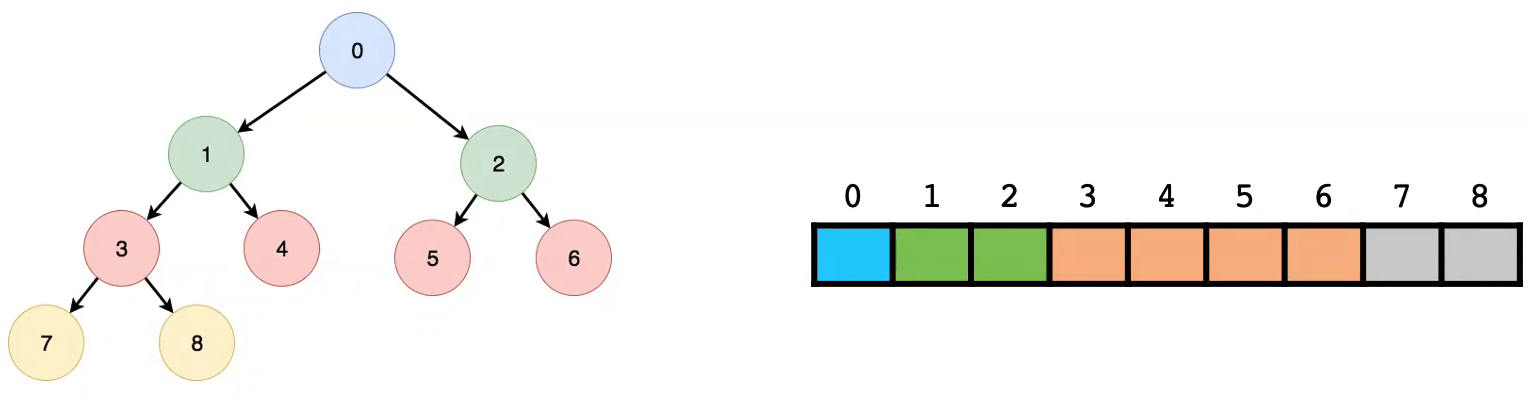
- 二叉树→数组的转换
- 按层序遍历的顺序存储在数组中,每一层的结点存储是连续的
- 这里是从0号存储的,也🆗,但不🆒
-
堆[优先队列]
本质思想是优先队列,但堆只是优先队列的一种实现方式;堆是在完全二叉树的基础上维护的
结构定义
- 结构与完全二叉树一样,但多维护了一种性质👇
- 大顶堆:对于任意三元组,根结点值最大
- 小顶堆:对于任意三元组,根结点值最小
结构操作
一切操作都要维护自己的性质!
- 尾部插入【+调整】
- 在尾部插入该元素,再自下向上调整,最远调整到根结点
- 在三元组里不断调整,依次与父结点比较,只要交换了就不停止,直到到达根结点
- 交换时只会改变交换元素的相对大小,整个结构的相对大小关系不变
- 比较的编号其实就是i 与 i / 2
- 时间复杂度:O(log[2]N),即树高
- 在尾部插入该元素,再自下向上调整,最远调整到根结点
- 头部弹出【+调整】
- 将最后一个元素拿到堆顶,再自上向下调整,直到该元素没有子结点
- 在三元组里不断调整,依次与孩子结点比较,只要交换了就不停止,直到没有孩子
- 为什么选择最后一个元素放到堆顶?
- 因为,如果拿其他位置的元素,谁来补这个元素的缺口呢
- 比较的编号其实就是i、2 * i 与 2 * i + 1
- 时间复杂度:同为树高
- 将最后一个元素拿到堆顶,再自上向下调整,直到该元素没有子结点
- [PS]
- 大顶堆:方便查找第1大和第2大的元素 [根结点、第二层中]
- 找第3大、第4大...就不那么简单,不方便确定所在层数
- ❗ 上面这个过程
- 队尾进元素,队首出元素👉同队列
- 而出队的元素是最值👉又名优先队列
- 大顶堆:方便查找第1大和第2大的元素 [根结点、第二层中]
堆排序
- 根据其性质,全部弹出,将得到一个排好序的序列
- ⭐思维转变:堆顶元素的弹出操作 ==> 堆顶元素与堆尾元素交换
- 【如此操作】
- 大顶堆的元素全部弹出👉原数组存储了一个从小到大的排序序列
- [至此,从大顶堆,得到一个特殊的小顶堆,因为一般将弹出元素放在原数组尾部]
- 时间复杂度:O(NlogN)
- 消耗的时间在于调整操作,每次调整的时间复杂度是O(logN),共N个元素,需调整N - 1次
- 弹出操作的时间复杂度是O(1)的
- 时间效率一定不会退化
建堆
【若要使用堆排序,首先需要维护一个堆,也就是用普通的序列建堆,下面有2种思路】
常规思路
又叫插入建堆法
- 按照前述尾部插入的调整方法:自下向上
- 从第0层 [默认根结点在第0层] 开始,计算每一层的最多调整次数:
-
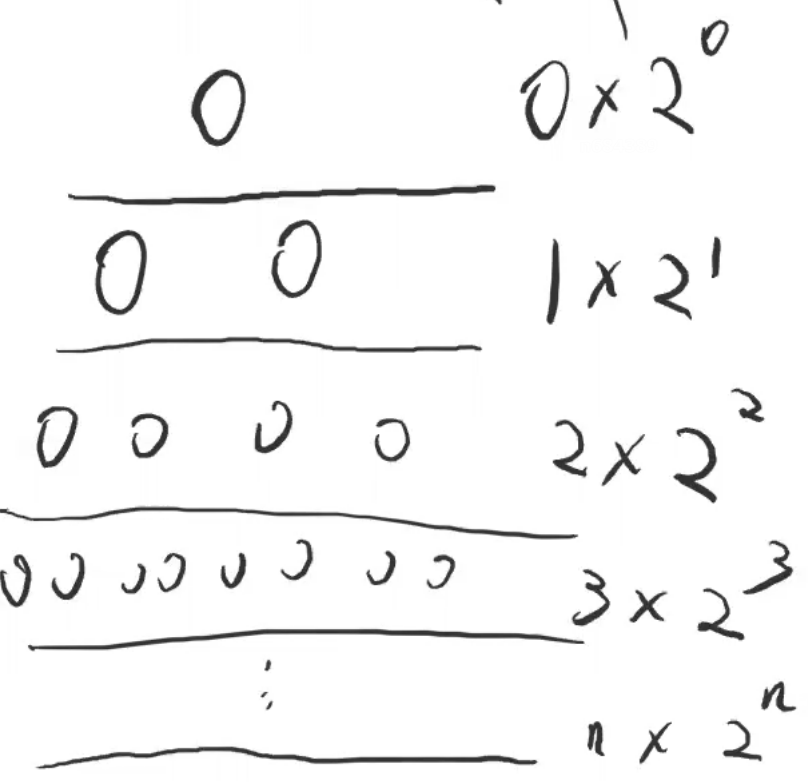
- 第 i 层元素的调整次数为 i,第 i 层的结点数为2 ^ i→ 第 i 层的总调整次数为 i * (2 ^ i)
- 最坏的建堆时间复杂度O(NlogN),计算过程如下:
- 总的调整次数 S = (n - 1) * 2 ^ (n + 1) + 1,过程如下:
-
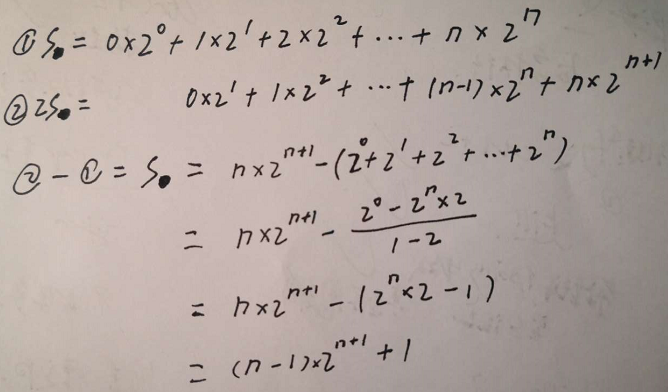
- 利用裂项相消法
-
- 上面的n对应【层数 - 1】 [从第0层开始,到第n层,层数为n+1],若令总的结点数为N,则n ≈ log[2]N
- ❗【层数n→结点数N的换算】将n ≈ log[2]N代入S,得到S ≈ Nlog[2]N
- 即最坏的时间复杂度为:O(NlogN)
- 总的调整次数 S = (n - 1) * 2 ^ (n + 1) + 1,过程如下:
线性思路⭐
也就是【线性建堆法】
-
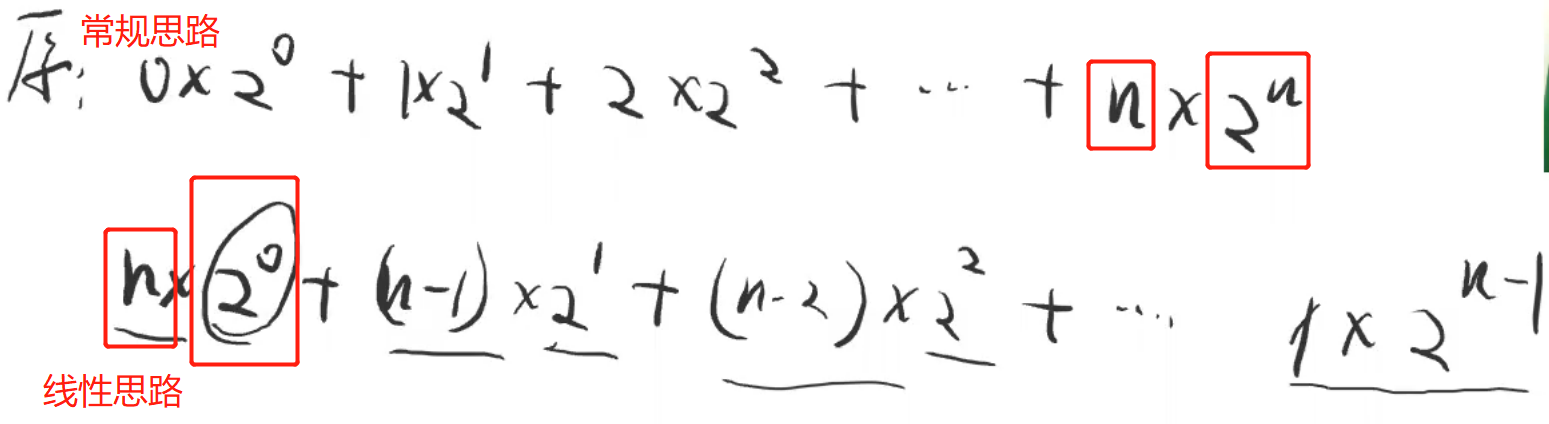
-
如图所示
- 常规思路:越到下面层,需要的调整次数越多,也就是权重越大
- ❗ 那是否可以思维反转,把大权重放到前面,让下面结点数多的层的权重减小
- 线性思路:可以!从倒数第二层开始排,【自上向下】调整
-
🆒最坏的建堆时间复杂度O(N)
- 同样利用裂项相消法得到总的调整次数 S = 2 ^ (n + 1) - 2 - n
- 把层数n换算到结点数N,得到S ≈ 2N - 2 - log[2]N
- 即最坏的时间复杂度为:O(N)
-
⭐推荐视频Linear Time BuildHeap——Youtube
- 比较了常规建堆和线性建堆两种思路,并有直观的动画演示,加深印象
代码演示
堆[优先队列]
-
-
-
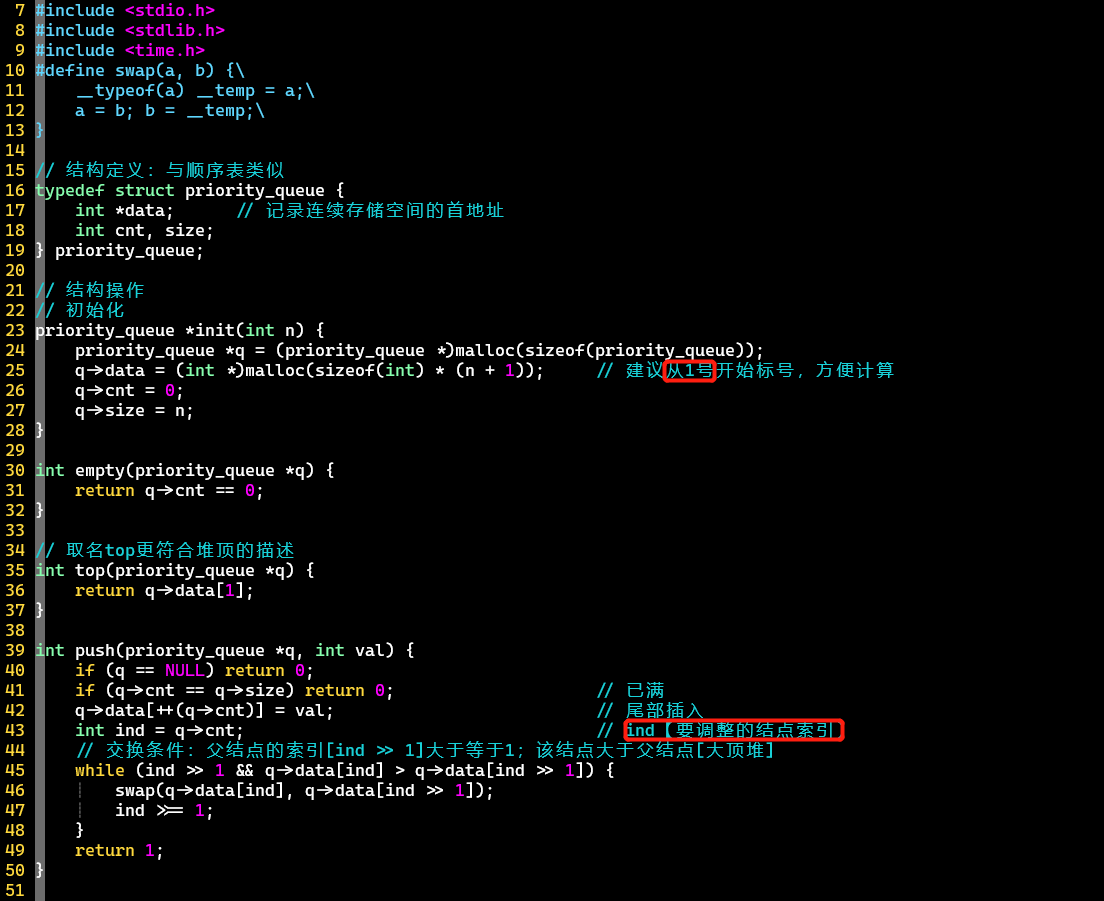
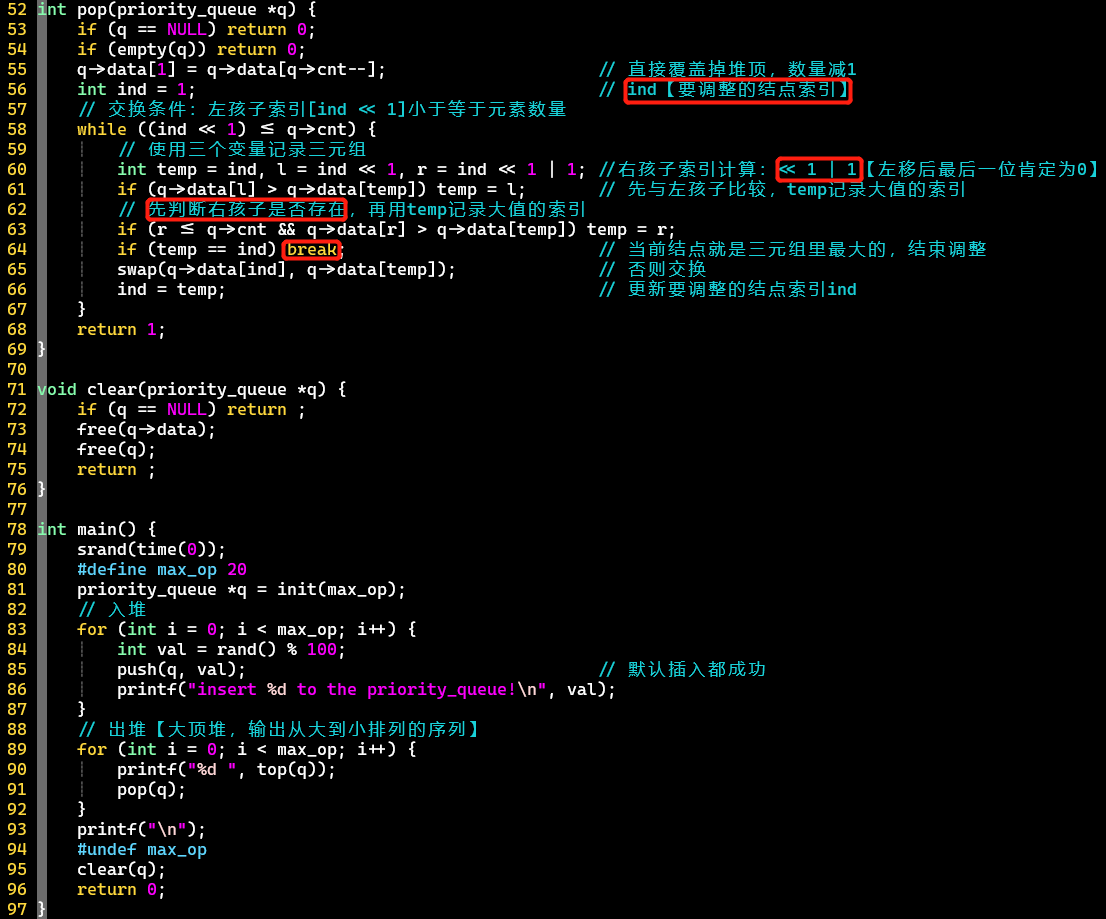
调整操作,巧妙使用变量ind,还有temp、l、r
- ind到一定条件就停止调整
- 注意判断ind[入堆、出堆]、r[出堆]是否存在
线性建堆法
-
-
-
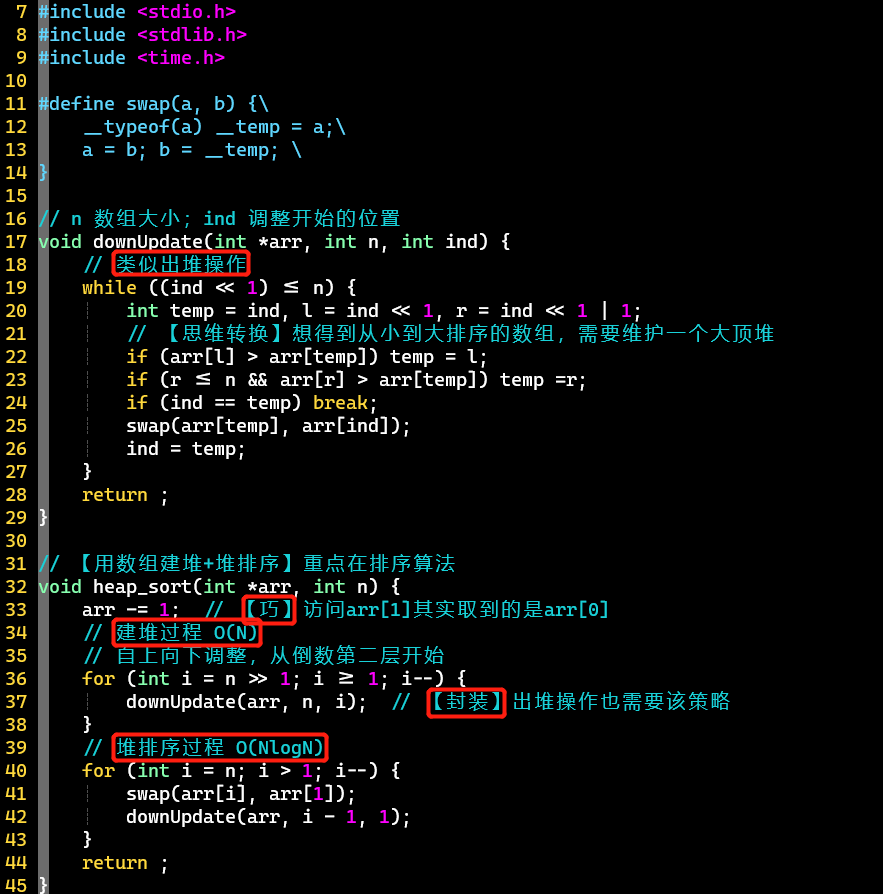
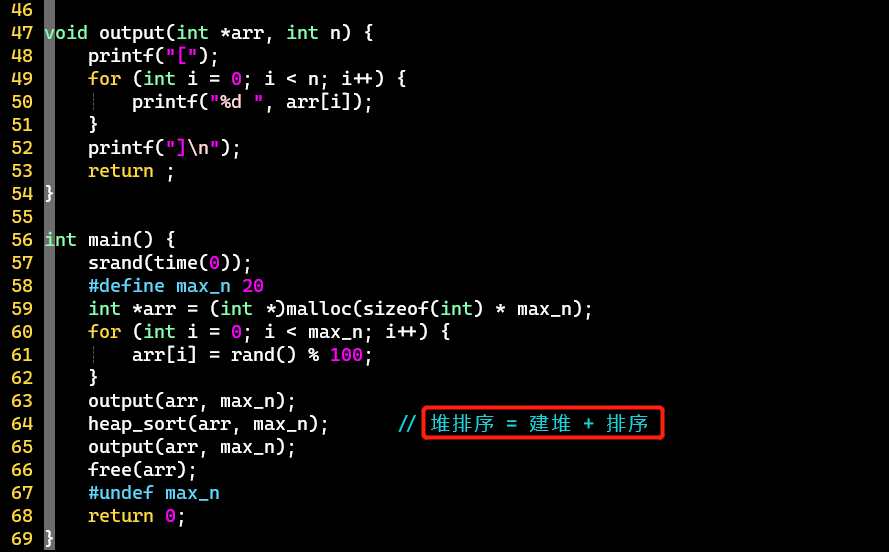
这里的【堆排序】考虑了【建堆】+【排序】
- O(N) + O(NlogN) = O(NlogN)
-
没有定义堆结构,用数组模拟堆
-
第33行:堆结点编号从1开始更方便,所以这里arr-1是让数组的索引统一向左偏移1个int大小
-
封装了自上向下的调整方法,从下图可以看出最先调整的位置,来自前面的推荐视频Linear Time BuildHeap——Youtube
-
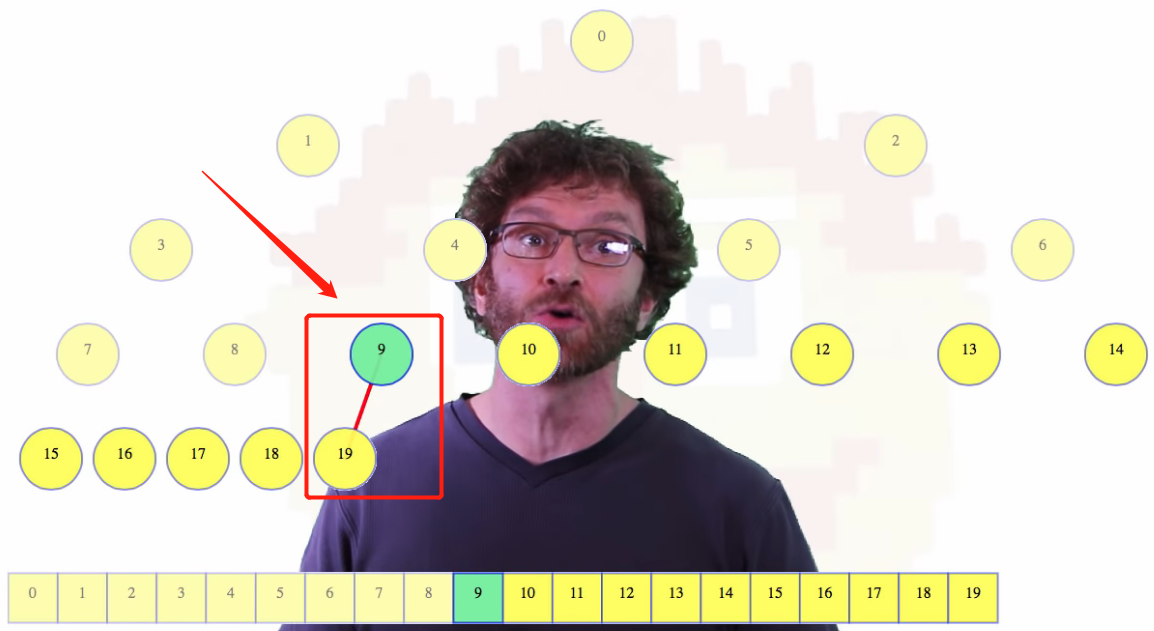
思考点
- ❌n层循环对应的时间复杂度就是O(N^n),要摈弃固化的思维,分析本质!
-