课程内容

• 并查集：合并集合[建立连通关系]、查找集合中的连通关系[判断某两个点是否连通]

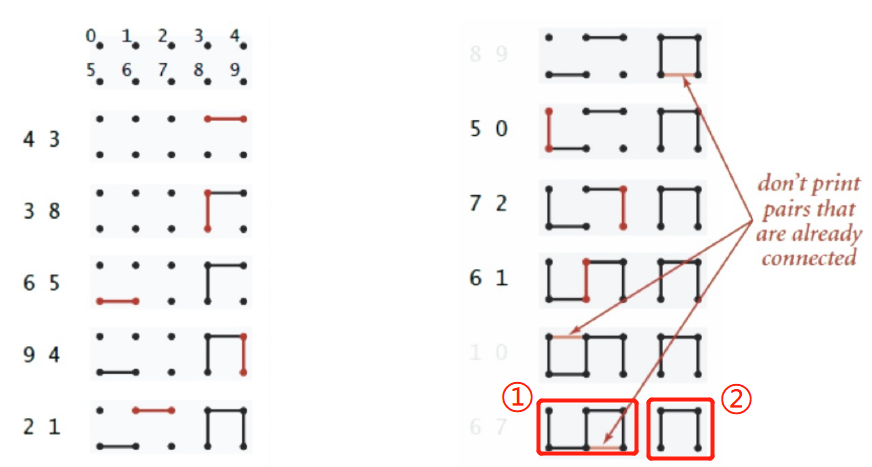
连通性问题

• 

• 规则：已经具有连通关系的点不能重复连接

• 将所有点分成了2个集合：①、②

• [PS] 点与点的关系(合并、判断连通)→也可以是→集合与集合的关系

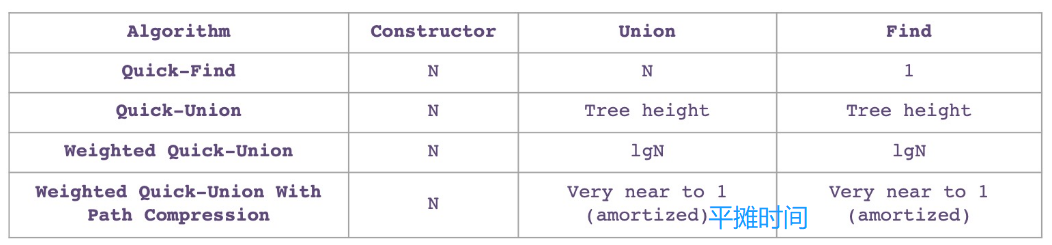
Quick-Find算法

• 核心思想：染色
  • 一个颜色，对应一个类别
  • 初始化：个体独立，都写成自己的索引，属于一个独立的集合里
  • ⭐把和自己连通的所有点的颜色改成要染的颜色
• 时间复杂度
  • 连通判断：O(1)——查找快，所以叫Quick-Find
  • 合并操作：O(N)——需要遍历所有的点才能确定是否要合并
• 🆒引发思考：为什么又叫森林呢？
  • 关键在于合并操作，几个点与几个点的合并，集合与集合的合并
  • 类似于子树与子树之间的合并，或是将一棵树作为另一棵树的子树
  • 所有的集合放在一起，类似于所有的树放在一起，就是森林
• 那么，除了染色还有其他方式吗？
  • 思考：染成了什么颜色并不重要，只需要知道和哪些点的颜色相同，即连通

Quick-Union算法

• 生活启发：找大哥，找领导
• 核心思想：找代表元素 [根结点]
  • 存的值就是其代表元素
  • 初始化：个体独立，都写成自己的索引，属于一个独立的集合里
  • ⭐找到两点的代表元素，修改其中一个代表元素里的值为另一个代表元素里的值
  • 代表元素：里面的值就是它自己
  • 联想：大哥或他的小弟叛变了，都从大哥开始叛变，叛变到另一个小弟的大哥那
    • 与Quick-Find的结果一样，都是把一棵子树整体合并到另一棵子树，不过是通过代表元素来实现的
    • 只能是根结点指向根结点
• 时间复杂度
  • 都得找根结点，与树高相关
  • 连通操作：O(树高)
  • 合并操作：O(树高)
  • ❗ 2种情况
    • 正常状态→均为O(logN)
    • 退化为一个链表→均为O(N)
• 对于退化情况，如何解决呢？👇

weighted Quick-Union算法

【按秩合并】

• 如何避免退化？→保证枝繁叶茂
  • 合并依据1：树高，矮树挂在高树下[两两结合]
    • 高度为 h 的树，至少需要的结点个数N为2 ^ (h - 1)
    • 即树高h = log[2]N + 1 ≈ log[2]N
    • [PS] 只有两棵一样树高的树合并，才会使高度增加
  • 合并依据2：结点数量，结点少的树挂在结点多的树下
  • 两种优化方式都能得到O(logN)，但是合并依据2【结点数量】更优秀一些
• ⭐为什么合并依据2更优秀
  • 【示例】什么是平均查找次数
    • 如下图所示，计算了A、B树的平均查找次数
    • 
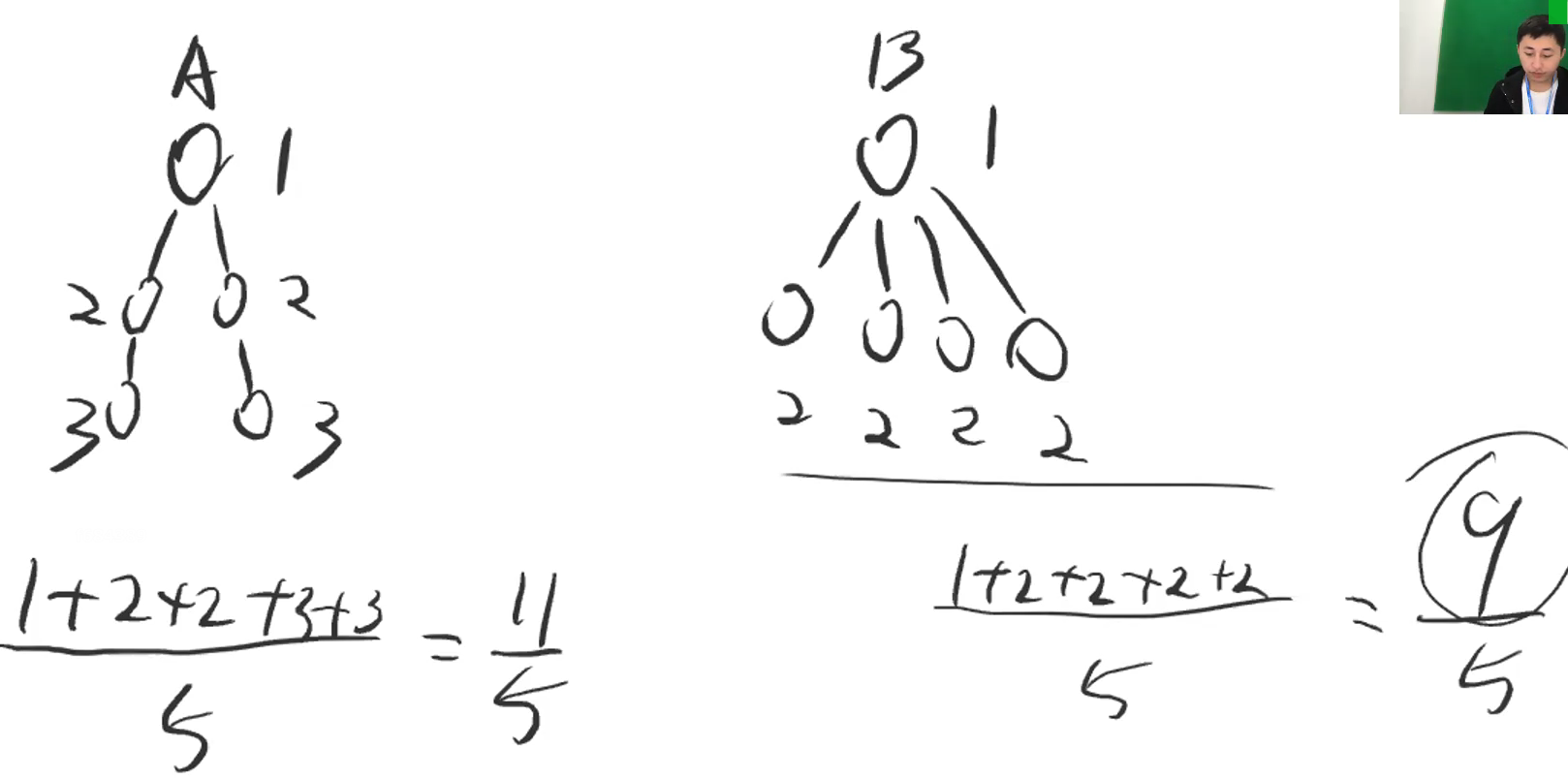
    • 结点深度即为结点的查找次数，平均查找次数 = 总查找次数 / 总结点数
    • 此示例，B树的查找操作更快
  • 【推导】合并依据2直接决定平均查找次数
    • 对于有SA、SB个结点的A、B树，它们的总查找次数LA、LB分别为：
      • 
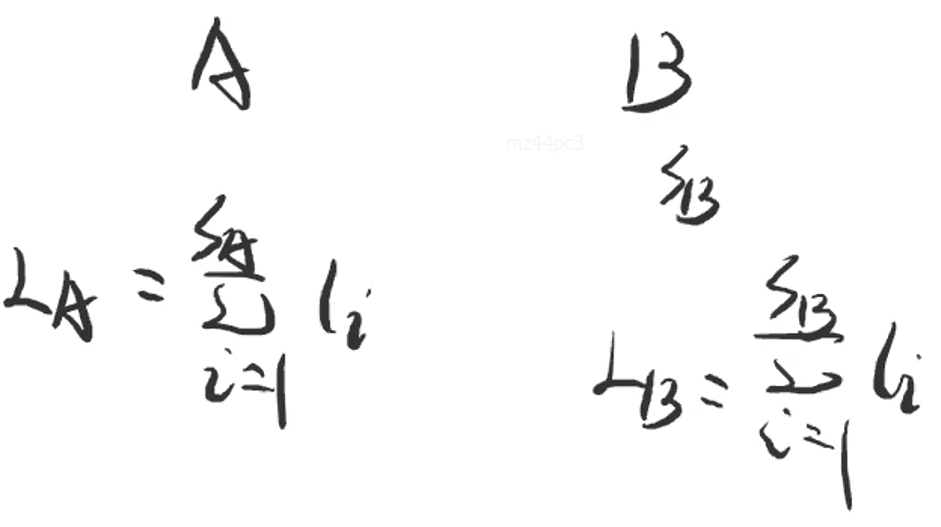
      • 其中，li 代表第 i 个结点的深度
    • 此时进行合并操作，分别计算①A→B和②B→A的平均查找次数
      • ①当A树作为子树合并到B树时，为
        • 
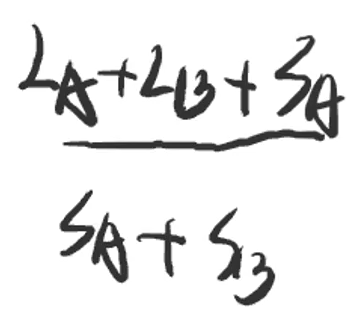
        • A树中的所有结点需要多查找一次
      • ②当B树作为子树合并到A树时，为
        • 
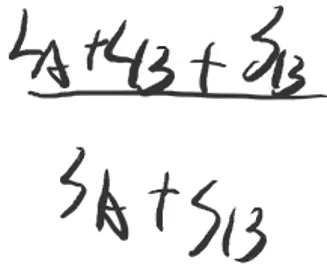
        • B树中的所有结点需要多查找一次
    • ❗【比较两种方式的平均查找次数】
      • 和树高[LA、LB]没有直接关系，而分子的结点数量[SA、SB]【直接】决定查找次数，次数越小越好
      • 👉谁的结点数少，就作为子树被合并
      • ❓思考：上面的推导是否证明高度无法作为合并依据呢？
        • ❌否，高度间接影响着结点数量，一般情况高度越低，结点数量越少
        • 但是，对于特殊情况，A树比B树高，而A树结点数量却比B树少时，还是按照【结点数量】作为合并依据，将A树作为子树合并到B树里
  • 所以以结点数作为合并依据更优秀！👇合并思路如下
• 在合并两棵子树时
  • 如果结点数一样，就按照普通Quick-Union的思路换
  • 如果不一样，结点数少的子树的根结点接在👉结点数多的子树的根结点下面
• [PS]换句话说
  • 在换大哥时
  • 如果小弟数量一样，就按照普通Quick-Union的思路换
  • 如果不一样，小弟少的大哥得跟👉小弟多的大哥混

+ 路径压缩

• 参考随堂练习2中weighted Quick-Union的可视化结果
  • 
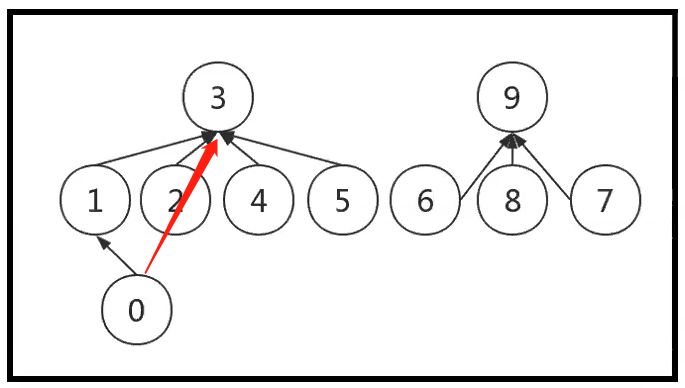
  • 0的位置有些尴尬
  • ❗ 不管0的代表元素为1还是3，并没区别，将0直接挂载3的下面，还能减小树高
  • 【方法】让每一个非根结点直接指向根结点，让结构扁平化

上述算法的效率比较

随堂练习

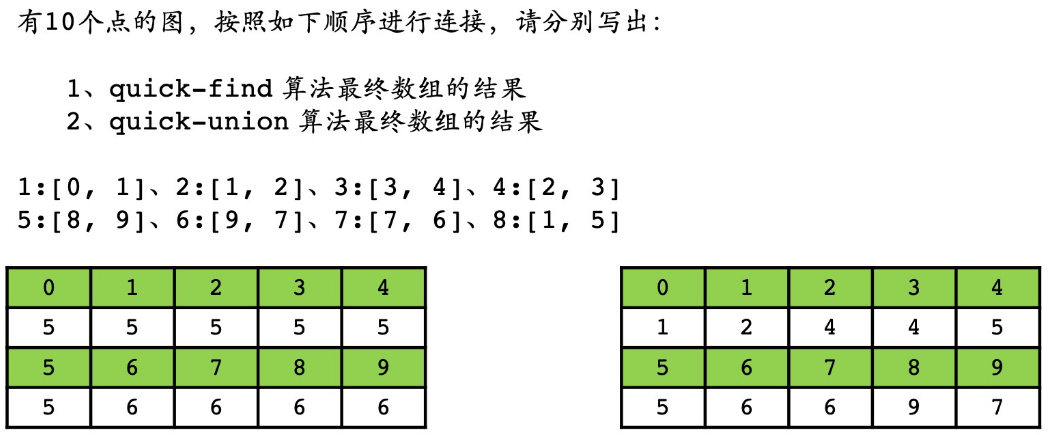
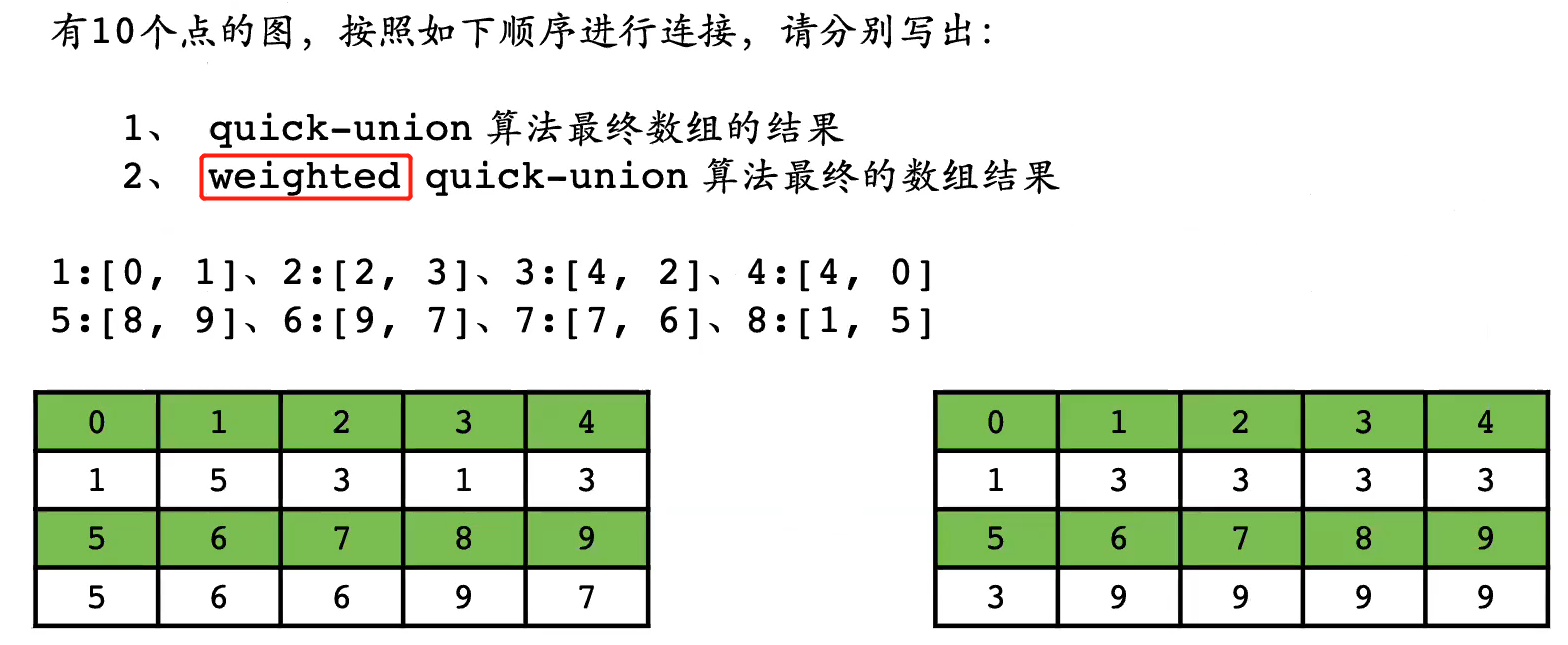
Quick-Find vs. Quick-Union

• 

• 【关键】理解Quick-Union

  • 0->1->2->4->5、3->4->5；8->9->7->6
  • 查找、合并边界：自己的代表元素就是本身时，停止

Quick-Union vs. weighted Quick-Union

• 

• 【关键】理解weighted的含义

  • 当两个集合的元素个数不一样时
  • 元素少的集合的代表元素的值👉元素多的集合的代表元素的值
  • 小弟少的大哥得跟着小弟多的大哥混

• 结果可视化

  • 
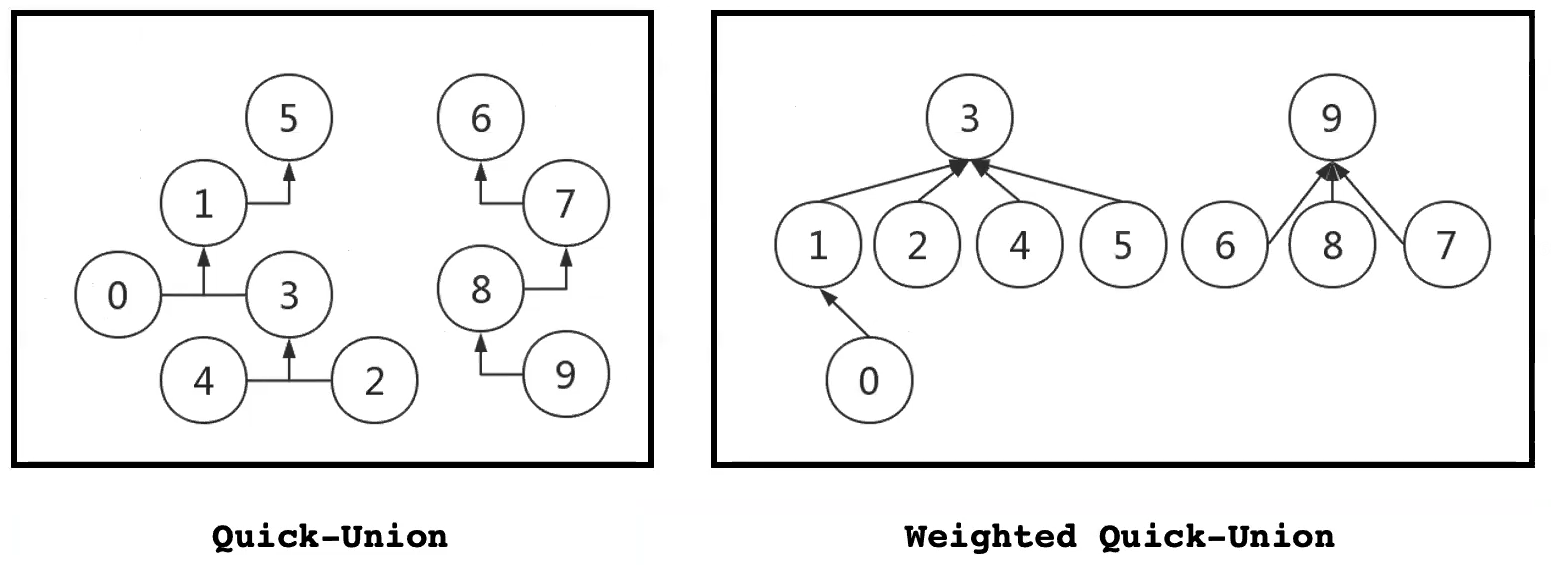
  • 很明显，weighted方法得到的树更矮，合并、查找效率更高

代码演示

HZOJ-71：朋友圈

样例输入

6 5
1 1 2
2 1 3
1 2 4
1 4 3
2 1 3

样例输出

No
Yes

• 思路
  • 使用数据结构——并查集
  • 1即合并操作，2即查找操作
  • 分别测试Quick-Find、Quick-Union [+weighted、+路径压缩、-weighted]的算法效率
• 代码

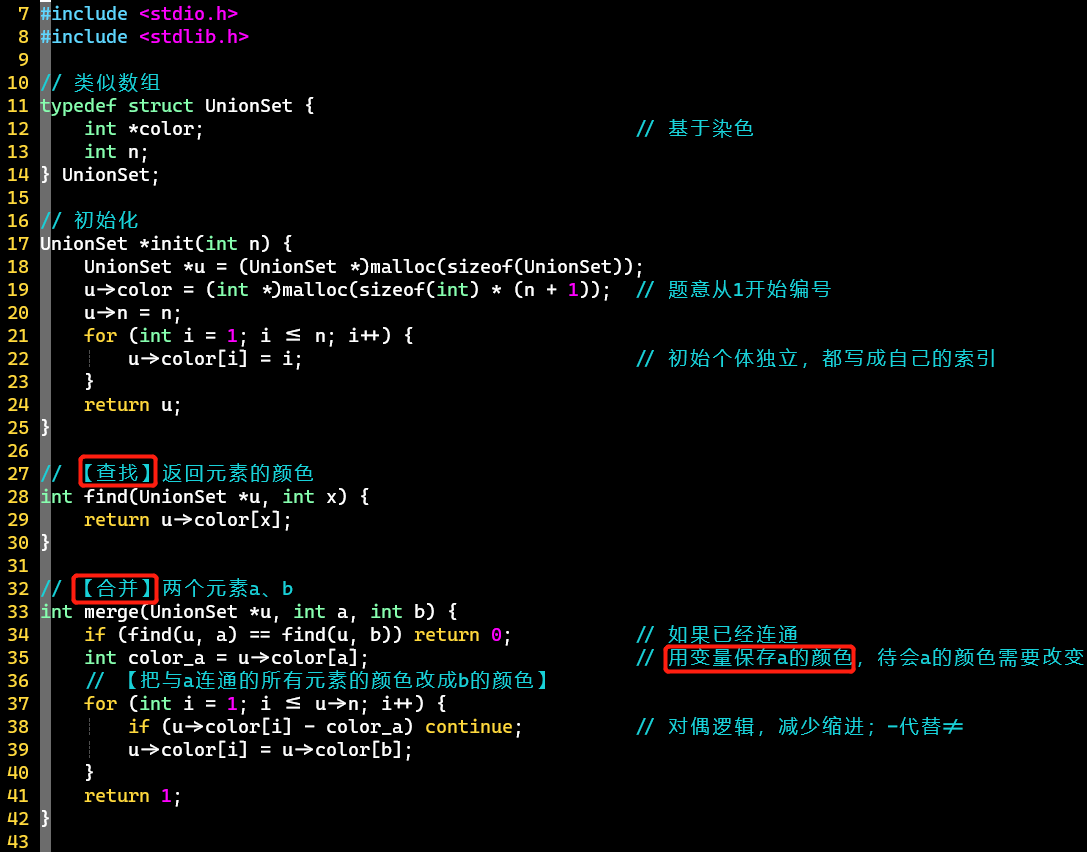
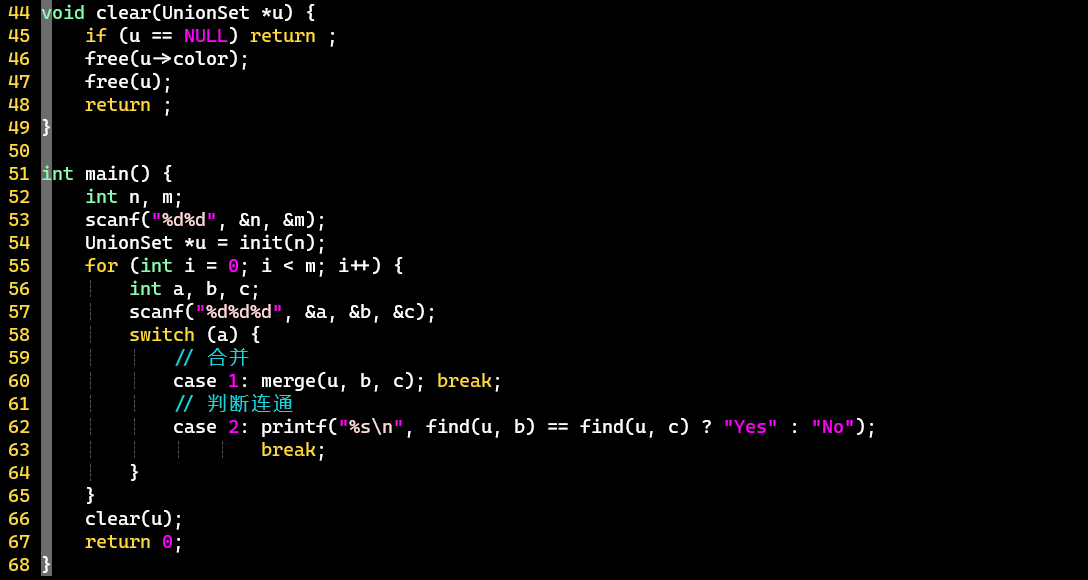
Quick-Find

• 
• 

• 查找、合并策略：基于染色

Quick-Union

• 

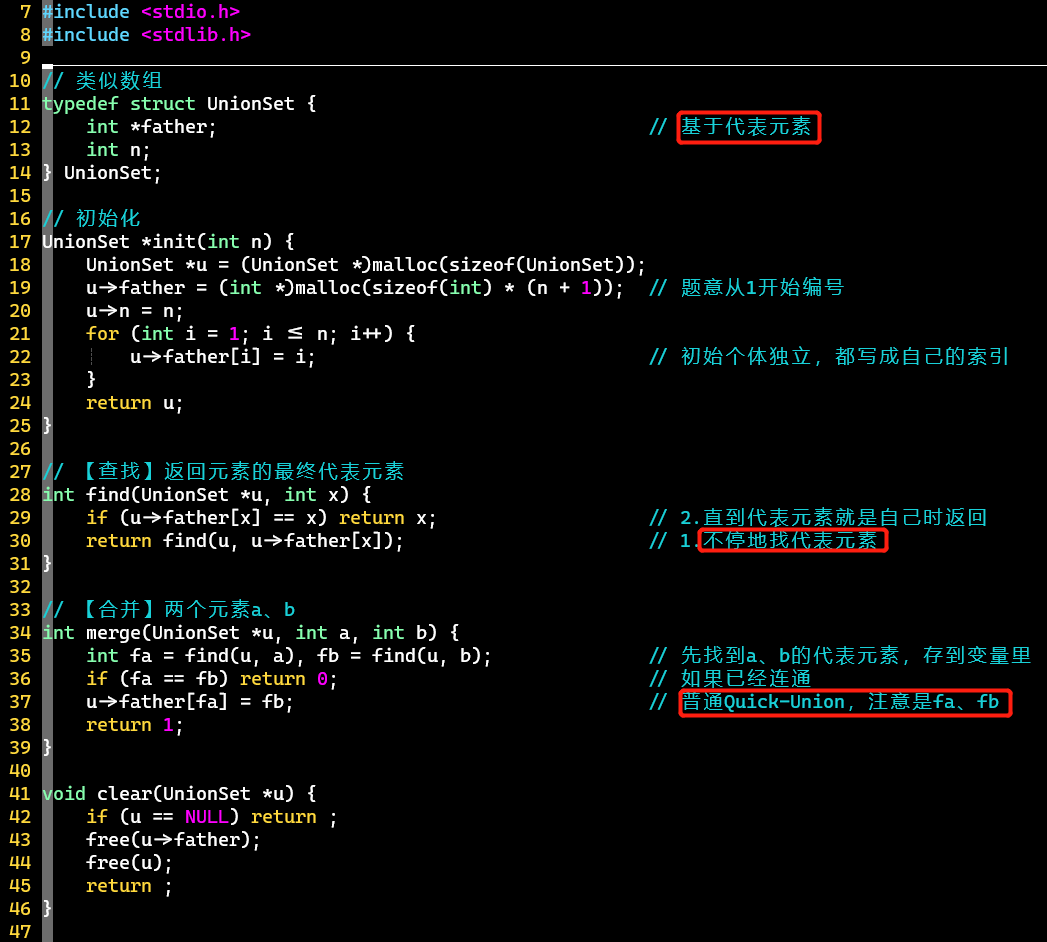
• 基于Quick-find

  • 修改结构定义的color为代表元素father
  • 修改查找操作：需要找到底
  • 修改合并操作：也要找到两个元素的底，才合并

• 易出现退化为链表的问题，下面进行优化

+ weighted

• 

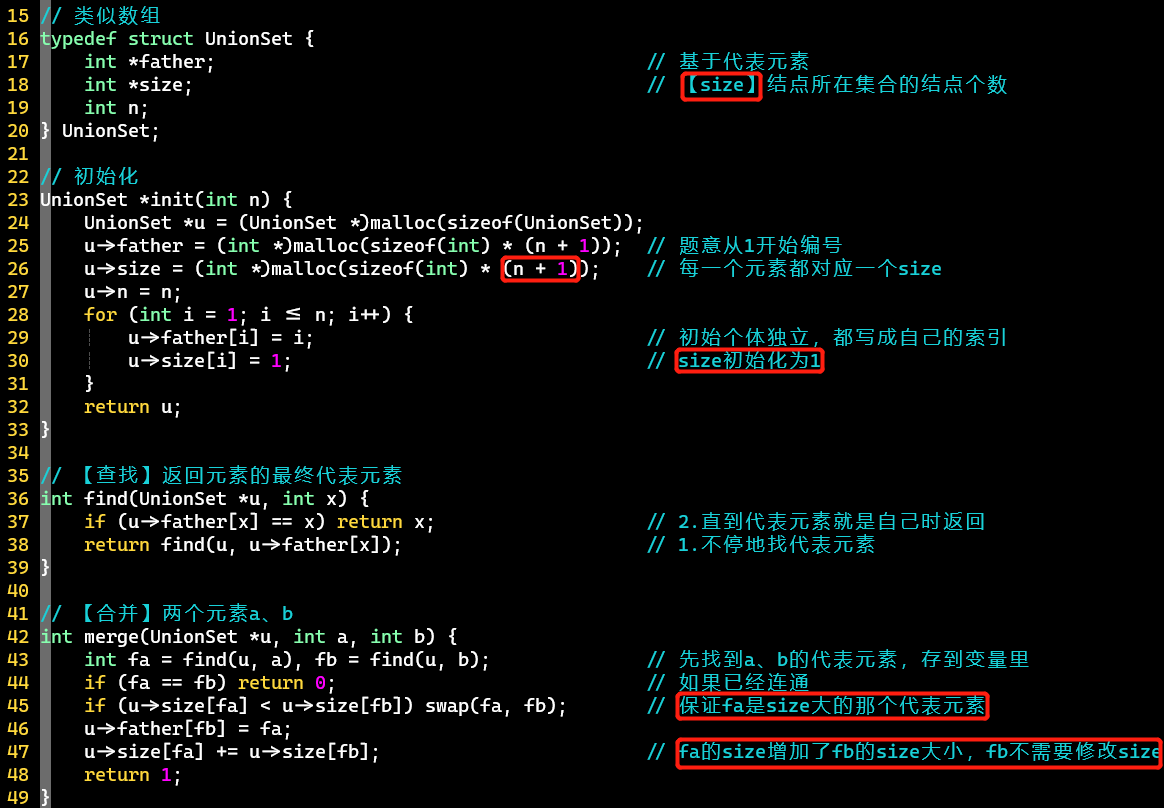
• 基于Quick-Union

• 添加size属性，记录结点所在集合的结点个数，以此作为合并策略

+ 路径压缩

• 

• 每次查找就会做一次路径压缩，将【查找元素】到【根代表元素】区间的所有元素都指向根代表元素 [根结点]

－weighted

• 
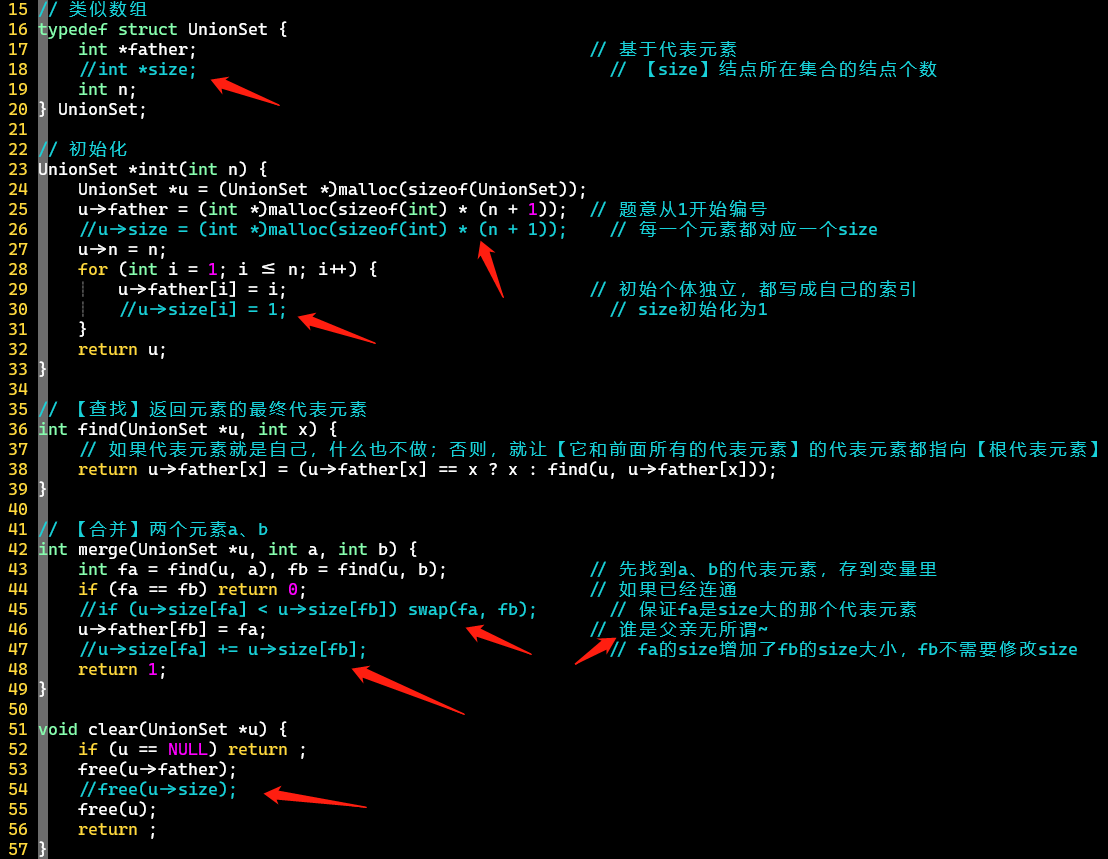
• 抹掉所有与size相关的操作
• 有了路径压缩后，不按秩合并[去除size属性]也能达到很好的效果

HZOJ平台上题目测试用时

• Quick-Union出现了退化问题
• 加了路径压缩后，不按秩合并也能达到很好的效果
• 🆒后三个方法都有不错的效果！

思考点

• 在weighted Quick-Union算法部分，结点数更优秀的推导是否证明高度无法作为合并依据呢？
  • ❌否，高度间接影响着结点数量，一般情况高度越低，结点数量越少
  • 但是，对于特殊情况，A树比B树高，而A树结点数量却比B树少时
    • 需按照【结点数量】作为合并依据❗ 将A树作为子树合并到B树里

Tips

• 《C++ Primer》建议当工具书使用
• 

课程速记