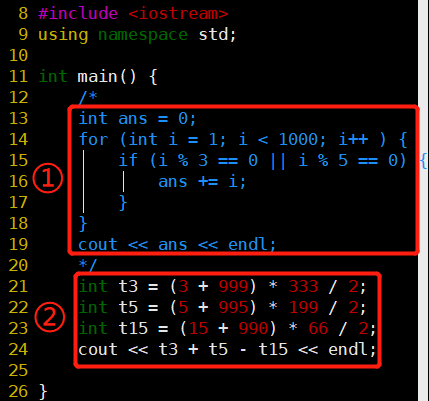
Euler-1:3或5的倍数

-
思路
- ①普通解法:遍历1-1000,判断能不能被3或5整除,可以就加入sum
- 时间复杂度:O(N)
- ②更优解:直接计算3或5倍数的和
- 利用等差数列,要注意有重复计算
- 公式:(首项 + 末项) * 项数 / 2
- 3~999的3的倍数和 + 5~1000的5的倍数和 - 15~985的15的倍数和
- 时间复杂度:O(1)
- 利用等差数列,要注意有重复计算
- ①普通解法:遍历1-1000,判断能不能被3或5整除,可以就加入sum
-
代码
-
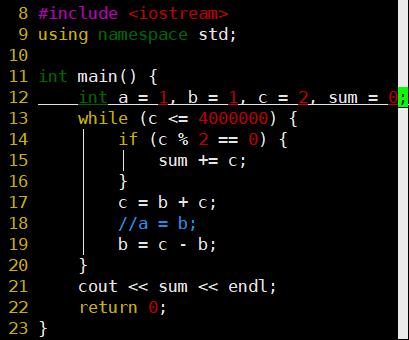
Euler-2:偶斐波那契数

-
思路
- 普通解法:用一个数组存储前面的值,递推,当是偶数时加入sum
- 空间复杂度:O(N),需要大量的额外空间
- 更优解:就用两个变量来回倒(老师说的是3个,实际a用不到)
- b、c:每次迭代,c = c + b; b = c - b;
- 空间复杂度:O(1)
- 普通解法:用一个数组存储前面的值,递推,当是偶数时加入sum
-
代码
-
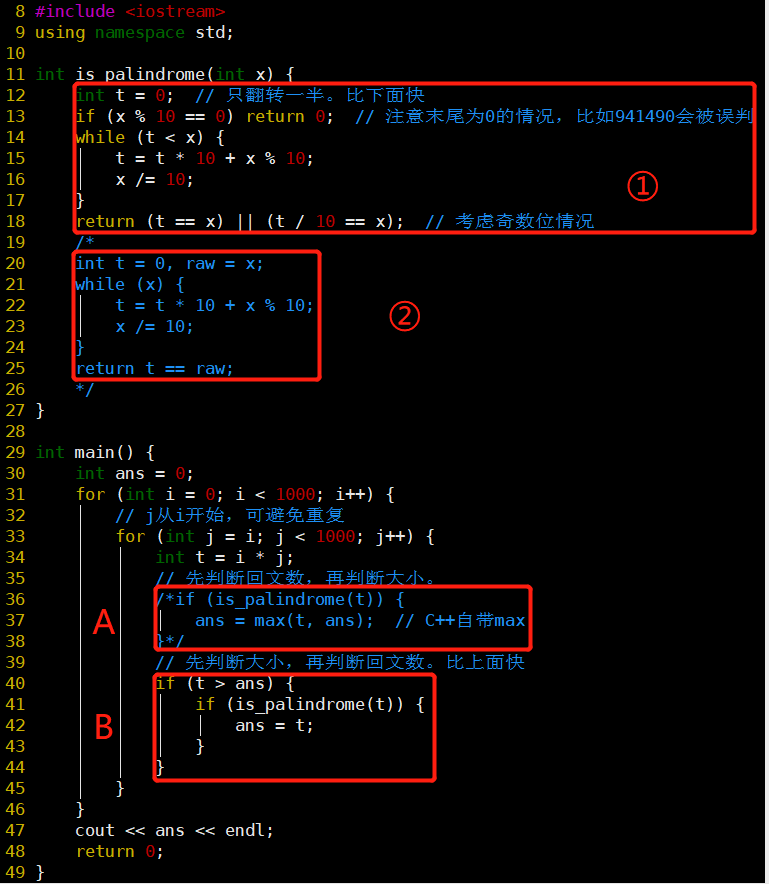
Euler-4:最大回文乘积

- 思路
- 判断回文数的思路
- 两个指针分别从头尾对应判等
- √更方便:把数字反过来,再做判等
- 其实还可以只反过来一半位数即可,循环成立条件是翻转的数字<剩余翻转的数字
- 但要注意:奇数位的情况;末尾含0的情况
- 其实还可以只反过来一半位数即可,循环成立条件是翻转的数字<剩余翻转的数字
- 枚举所有的3位数相乘,判断回文数,找最大
- 判断回文数的思路
- 代码
-
- 使用time *./a.out分别计算两两组合的时间花费
-
| time | ① 只翻转一半位数 | ② 翻转全部位数 |
|---|---|---|
| A 先判断回文数 | 0.013 | 0.017 |
| B 先判断大小 | 0.005 | 0.005 |
-
- j从i开始,可以避免重复乘积
- C++自带max函数
- 此外,利用短路原则还可以优化B,速度还有提升:0.004s

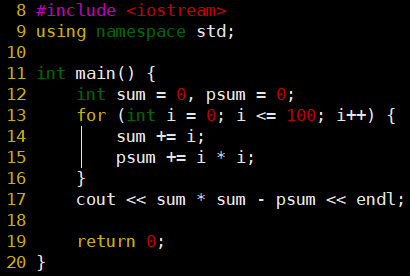
Euler-6:和的平方与平方的和之差

- 思路
- 简单循环:分别计算1~100的平方和、和,再用和的平方 - 平方和即可
- 代码
Euler-8:连续数字最大乘积
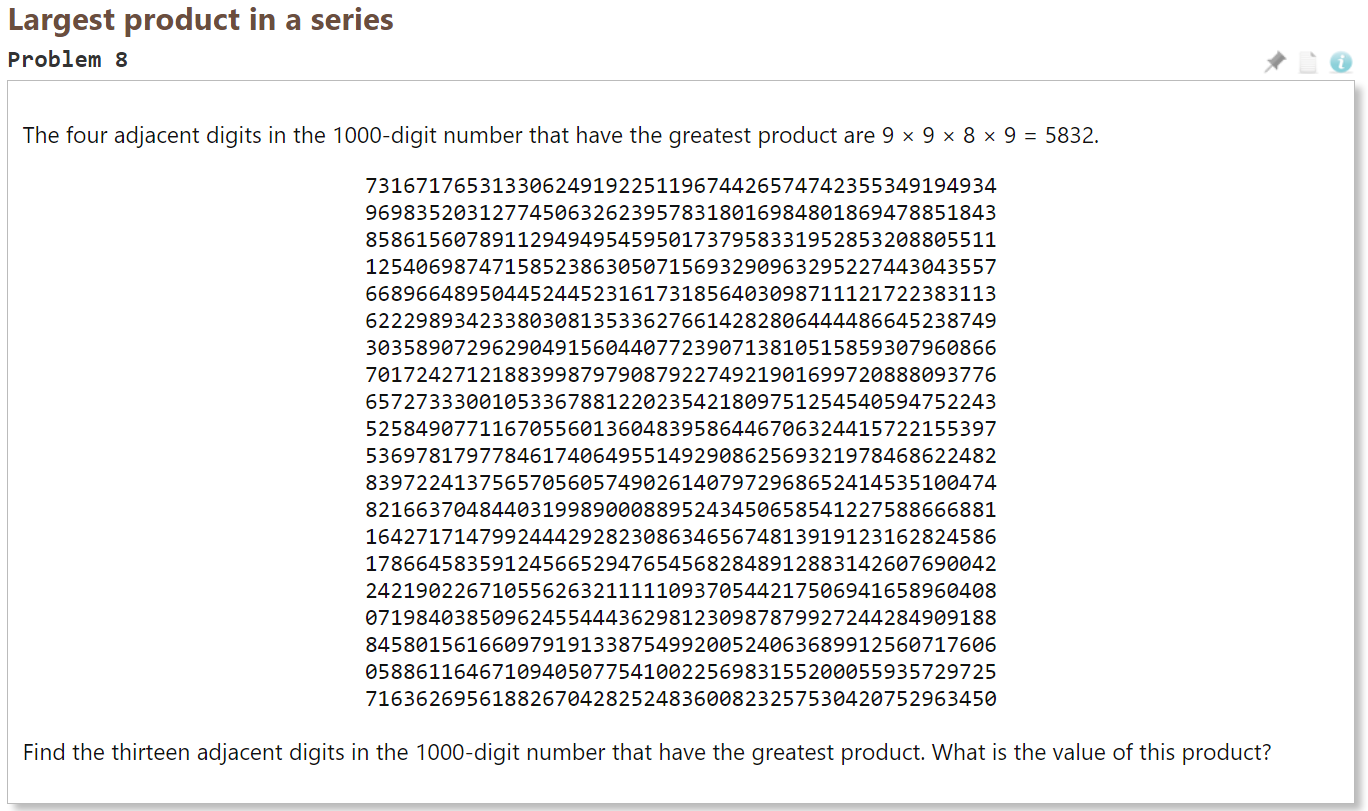
- 思路
- 首先将数据复制,保存在本地为字符串
- 检查复制后的格式:删掉空格、换行
- 读入时用数组存储,读取每位时需转换为数字(- '0')
- 滑动窗口法
- 静态窗口:固定窗口大小
- 动态窗口:一般称为双指针
- 解法:使用滑动窗口法——静态窗口
- 只需考虑窗口进的数和出的数,可以减少运算次数
- 出:除以
- 进:乘以
- 注意值是否为0
- 只需考虑窗口进的数和出的数,可以减少运算次数
- 代码
-
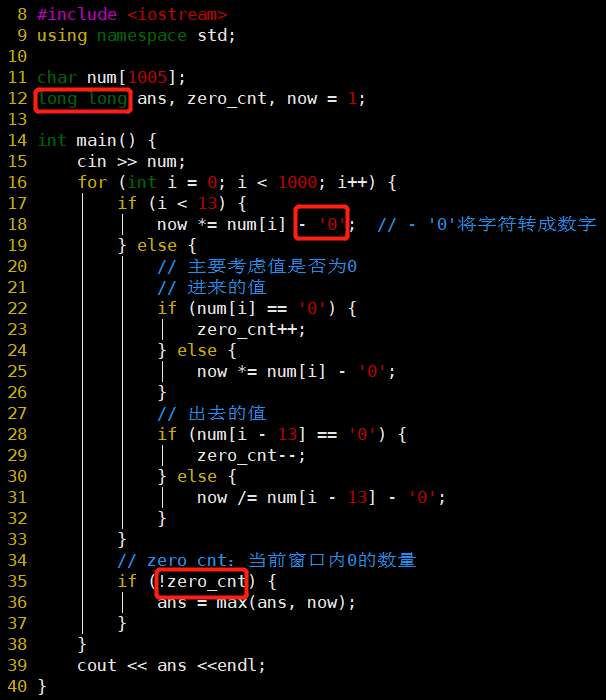
- 前13位不含0,可以直接计算now
- 注意窗口内0的情况
- ❗定义一个0的计数器
- ❌是否可以碰见0就将乘积变为1?
- 不行,需要存除除0以外数的乘积
- ❌是否可以将0直接变为1?可以减少判断次数,只需要对进来的值判断0
- 但这样是不可以的,因为有可能不满13位的两个0之间的数很大
- 比如11022340111111111111111111
- 执行时报错:floating point exception
- 除以0了可能会导致该错误
- 错误地估计了上界,9^13肯定超过了int类型的上界,所以使用long long
-
- 首先将数据复制,保存在本地为字符串

Euler-11:方阵中的最大乘积
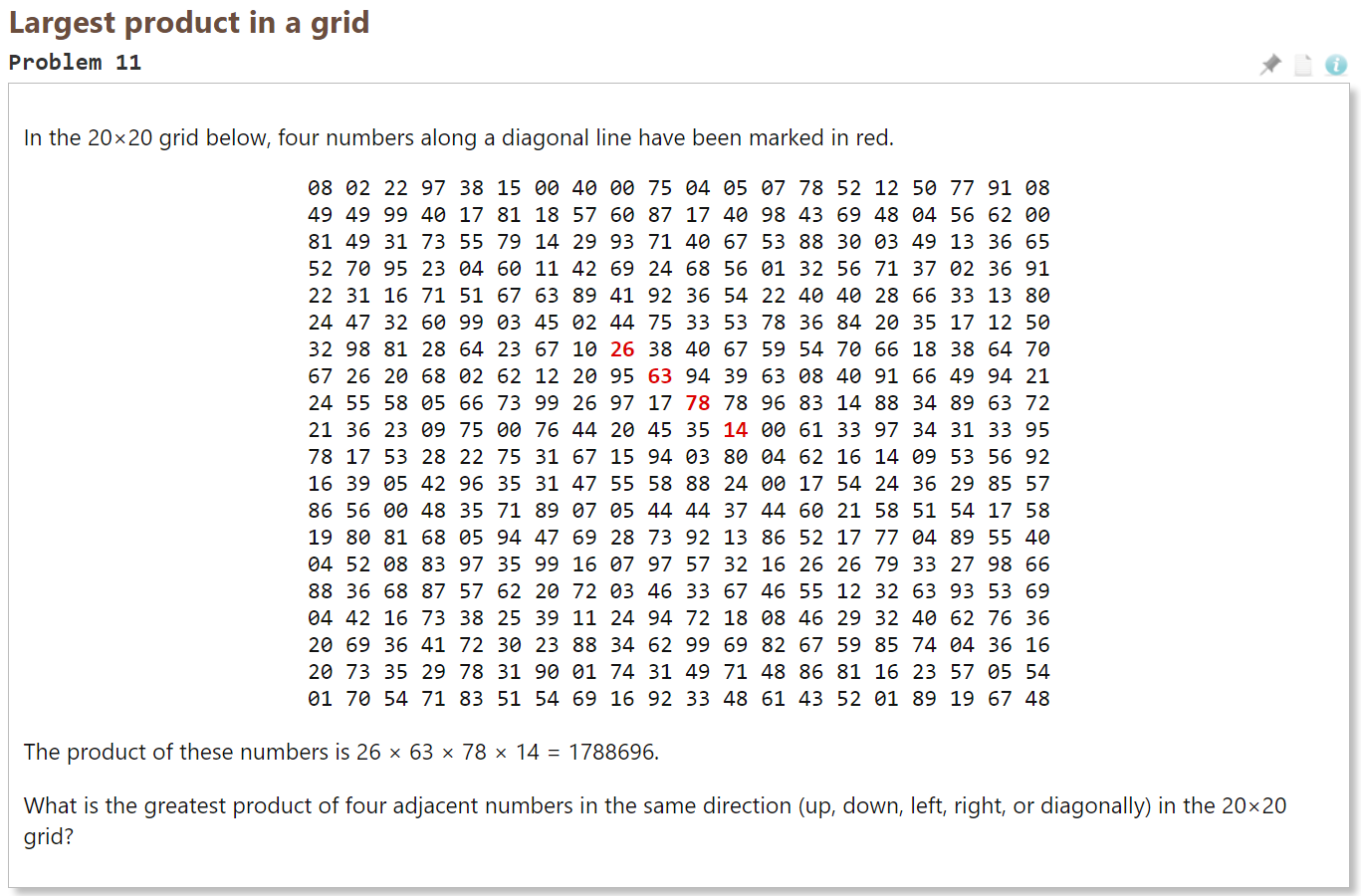
- 思路
- 方向数组
- 通过矩阵中的一个数的坐标,推算出某个方向的数的坐标
- 计算某个数各个方向的连续4个数的乘积,找出最大值
- 计算问题:只需取连续的4个方向来计算。避免重复计算
- 边界问题:①判断边界;√②边界补0(至少3圈0)。解决越界问题
- 方向数组
- 代码
-

- 学会定义方向数组
- 利用变量 l 控制某方向的第 l 位
- 在C语言循环中写声明变量的语句,编译器只会创建一次。如32、33行
- 参考C语言之重复声明变量-CSDN
-
Euler-14:最长考拉兹序列(记忆数组)
-

-
斐波那契数列
- 两种方法:递归、递推
- 递归
- 常规
- 很慢,因为有重复计算,但有优化版👇
- 使用记忆数组
- 递归+记忆化 ≈ 递推
-
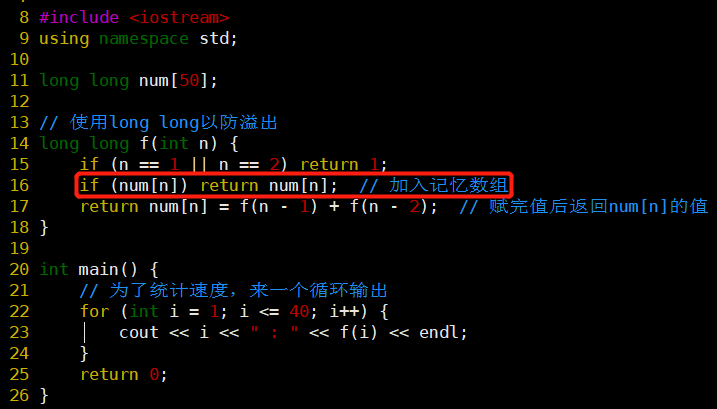
- 记忆化前→后:1.804s→0.002s
- 常规
- 递推:速度快,也占用空间,是不是可用euler2里的两个变量来回倒?
- 数组存储;num[i] = num[i - 1] + num[i - 2];
-
思路
- 同样利用递归 + 记忆数组
- 注意题中注:序列开始生成后允许其中的项超过一百万
- 不需要额外的计数器,可在每次计算下一个数时+1
-
代码
-
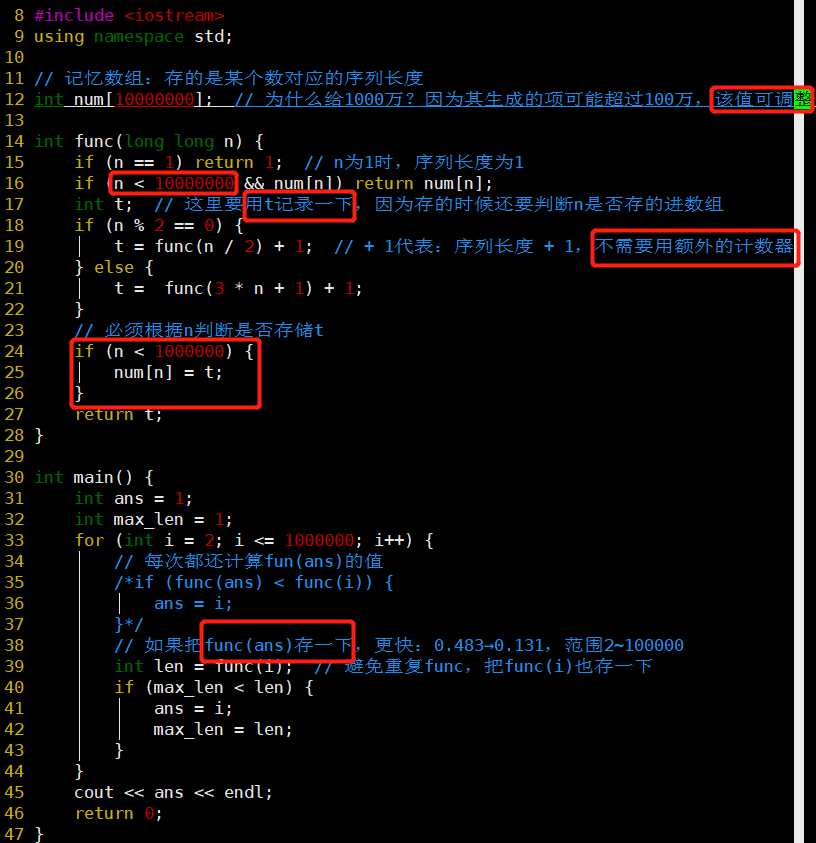
- 详见标注
- num数组长度越大,速度越快,空间消耗也越大
- 用t记录函数结果,好在存进数组前做一个判断
- main函数里把func(ans)值先存一下可以加快速度
-
Euler-13:大和(大整数加法)
- 思路
- 参照大整数加法
- 代码
- 参照大整数加法
➕大整数加法
- 大整数:用long long也存不下,一般用字符串存储
- ⭐数组方法
-
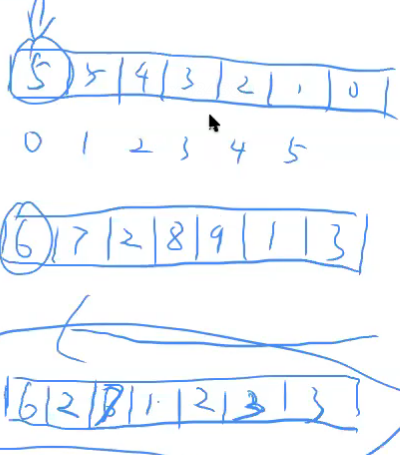
- 两个数组倒着存储大数,数组第0位存储大数的位数👉
- 如果不倒着存储,在最高为进位时不好处理?也可以直接输出不处理
- 但是不倒着存储,会有低位对齐的问题,不好处理
- 对每个索引里的值求和,和的位数取两个大数的最大位数👉
- 处理进位,如果是最后一位进位,记得将和的位数+1👉
- 倒着输出
-
- 代码
-
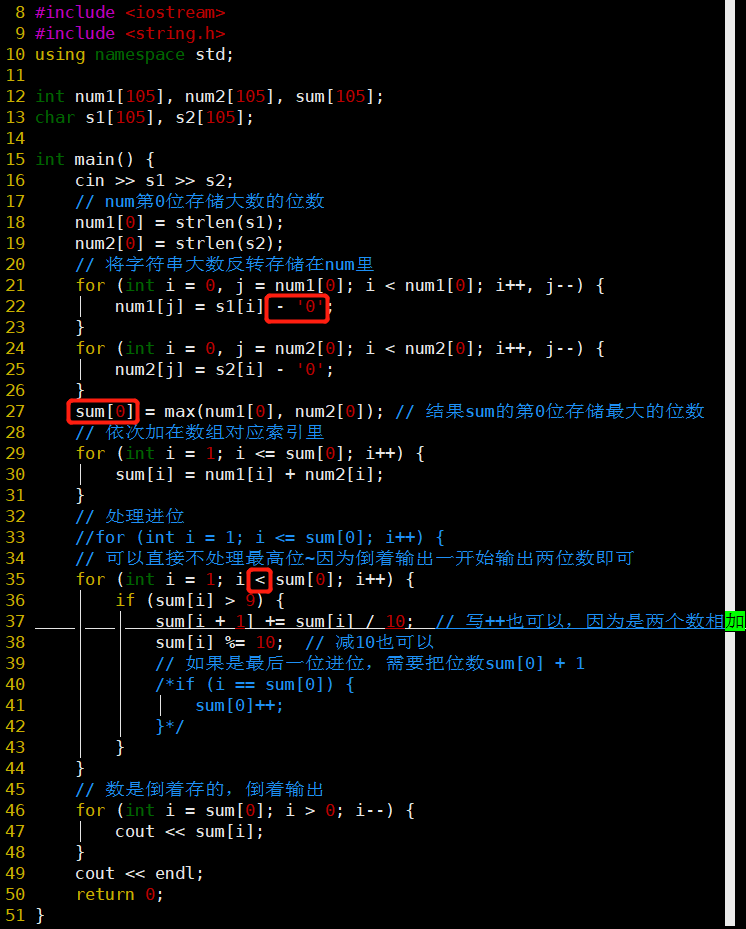
- 可以不处理最高位进位的情况,最高位有进位时直接第一次输出一个两位数
- 例如:输入888 + 222;输出11 1 0
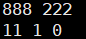
- 不过对于多个数相加可能普适性不好!一个索引存储1位数字最保险
-
Euler-25:一千位的斐波那契数(大整数加法)
-

-
思路
* 两个变量里的大整数循环加即可
* int num[2] = {1}; // 剩下的自动填充0 -
代码
-

✖ 大整数乘法
- 思路
- 类同大整数加法
- 每一位的乘积结果相加的位置:i + j - 1
- 代码
-
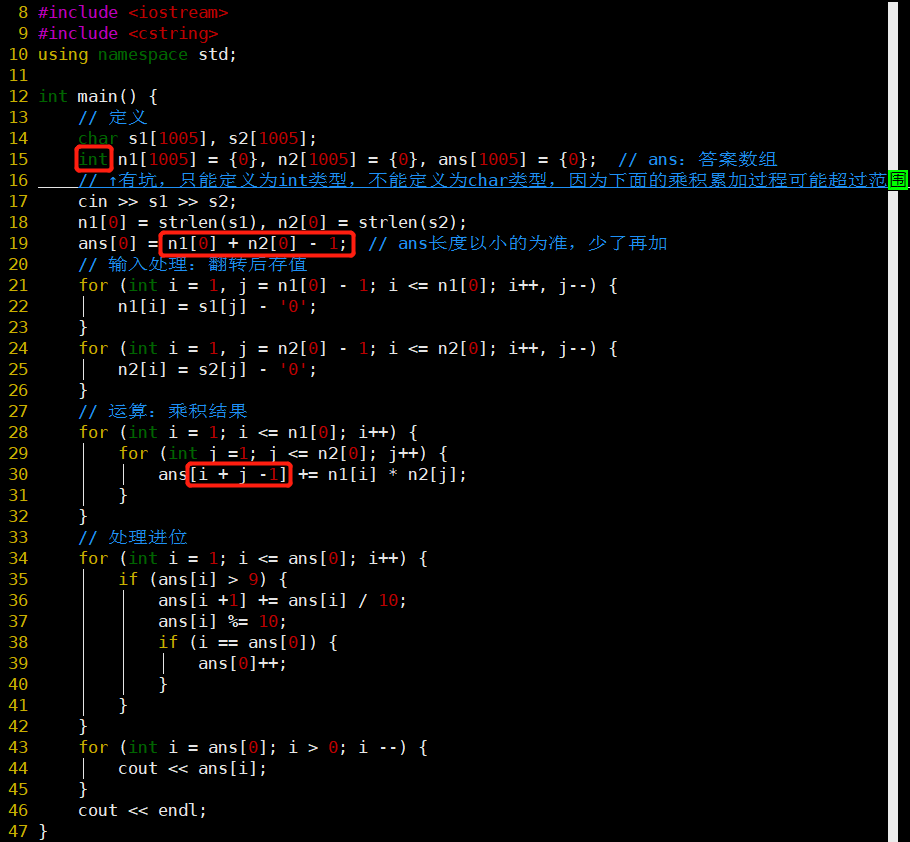
- 答案数组的元素类型至少是int
- 答案数组的长度取可能结果短的长度
- 乘积运算累加的位置要注意~
-
- 可尝试做欧拉计划16、20题
➗大整数除法
- 除数和被除数都是大整数
- 思路
-
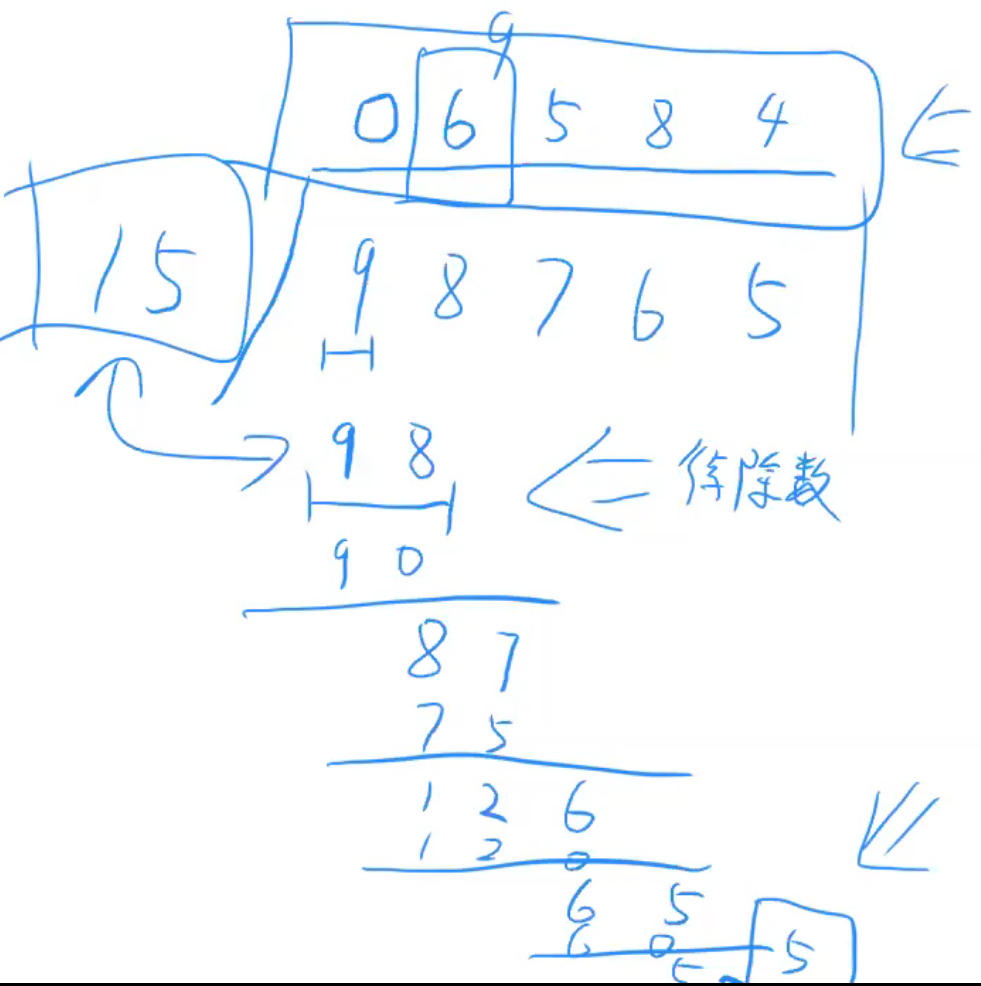
- 首先判断被除数是否大于除数
- 然后用待除数一直减除数,直到不能减为止,最多减9次
- 除数也可能是大整数,所以待除数也是大整数:这个会导致代码很复杂
-
- 可尝试hzoj 475、476题
Euler-15:网格路径(递推、通式)
- 思路
- 方法一:递推(动态规划)
-
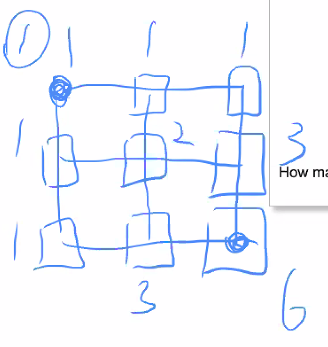
- 当前方案数 = 上面来的方案数+左边来的方案数
- 补0大法:从(1, 1)点开始存
- 注意边界:对于2 * 2的网格,左上角和右下角为点(1, 1)、点(3, 3)
- PS:也可以用递归+记忆化,有些相似
-
- 方法二:通式做,排列组合!
- 对于2 * 2的网格
- 往下和往右走的总步数是4,其中往下走2步,往右走2步
- 其实就是排列组合,C(4)2 = 4! / [2! * (4 - 2)!]
- 所以本题就是C(40)20
- 方法一:递推(动态规划)
- 代码
-
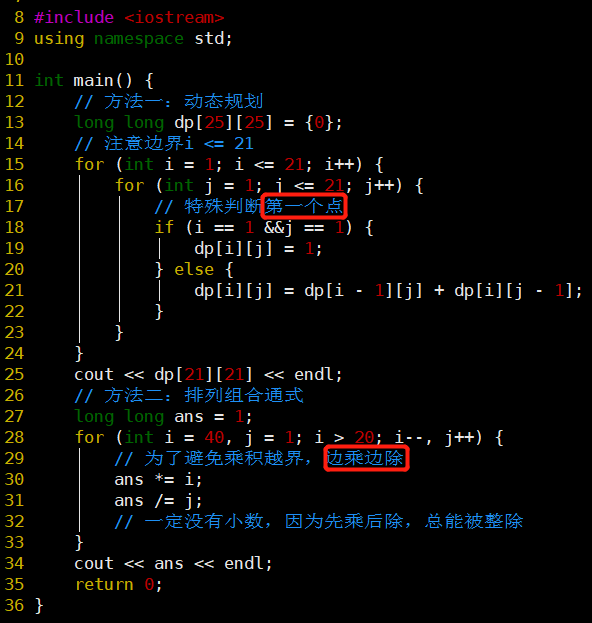
- 方法一要记得特殊判断第一个点(1, 1)
- 方法二边乘边除就不会越界,先乘再除不会有小数情况
-
Euler-18:最大路径和(树塔问题)
-

-
思路
- 递推(动态规划)
- 自上而下
- dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + num[i][j]
- 遍历最后一行,输出最大值
- 自下而上
- dp[i][j] = max(dp[i + 1][j + 1], dp[i + 1][j]) + num[i][j]
- 最后不需要遍历,最上头就是最大值
- 自上而下
- 补0!
- 递推(动态规划)
-
代码
-
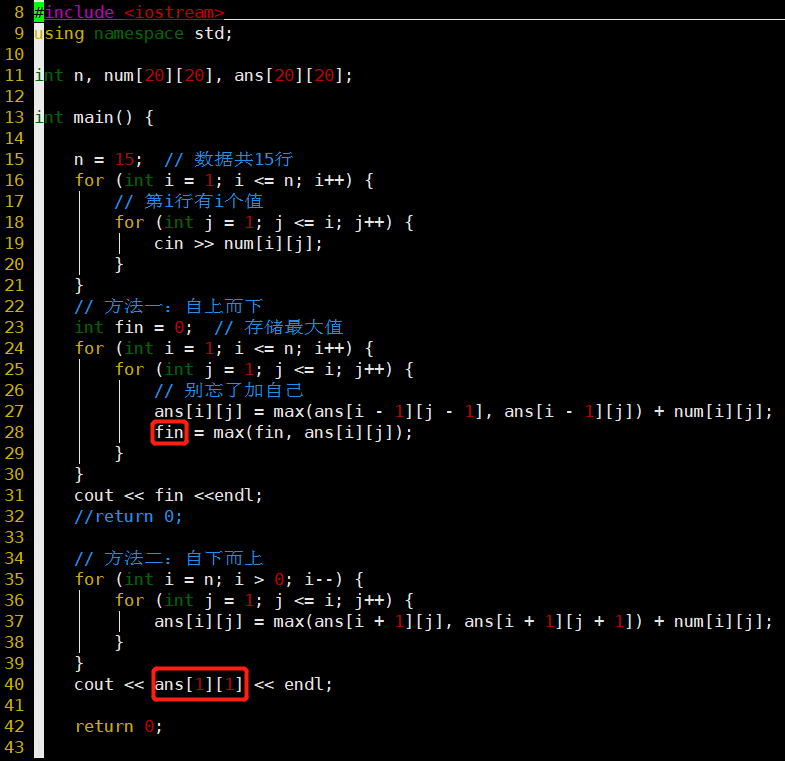
- 第i行有i个值
- 自上而下、自下而上方法的主要区别在于最大值的位置确定
-
HZOJ-590:树塔狂想曲
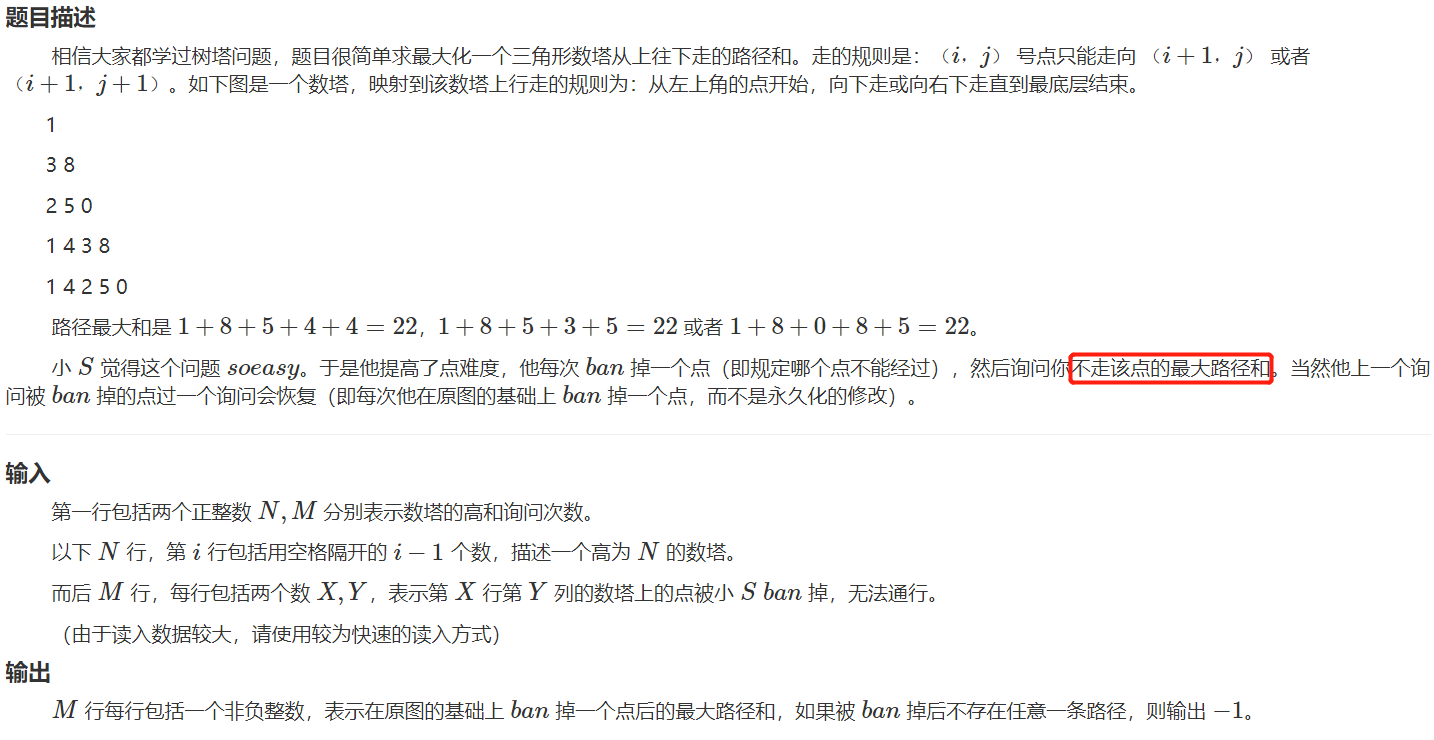
样例输入
5 3
1
3 8
2 5 0
1 4 3 8
1 4 2 5 0
2 2
5 4
1 1
样例输出
17
22
-1
-
思路
- ❌每次特殊处理一个点后,重新计算
- 记录每一个点对应的最大路径和与次大路径和
- 经过某个点能获得的最大值:自上而下 + 自下而上 - 当前值
- 时间、空间开销都是O(N^2)
- 思路图如下
-
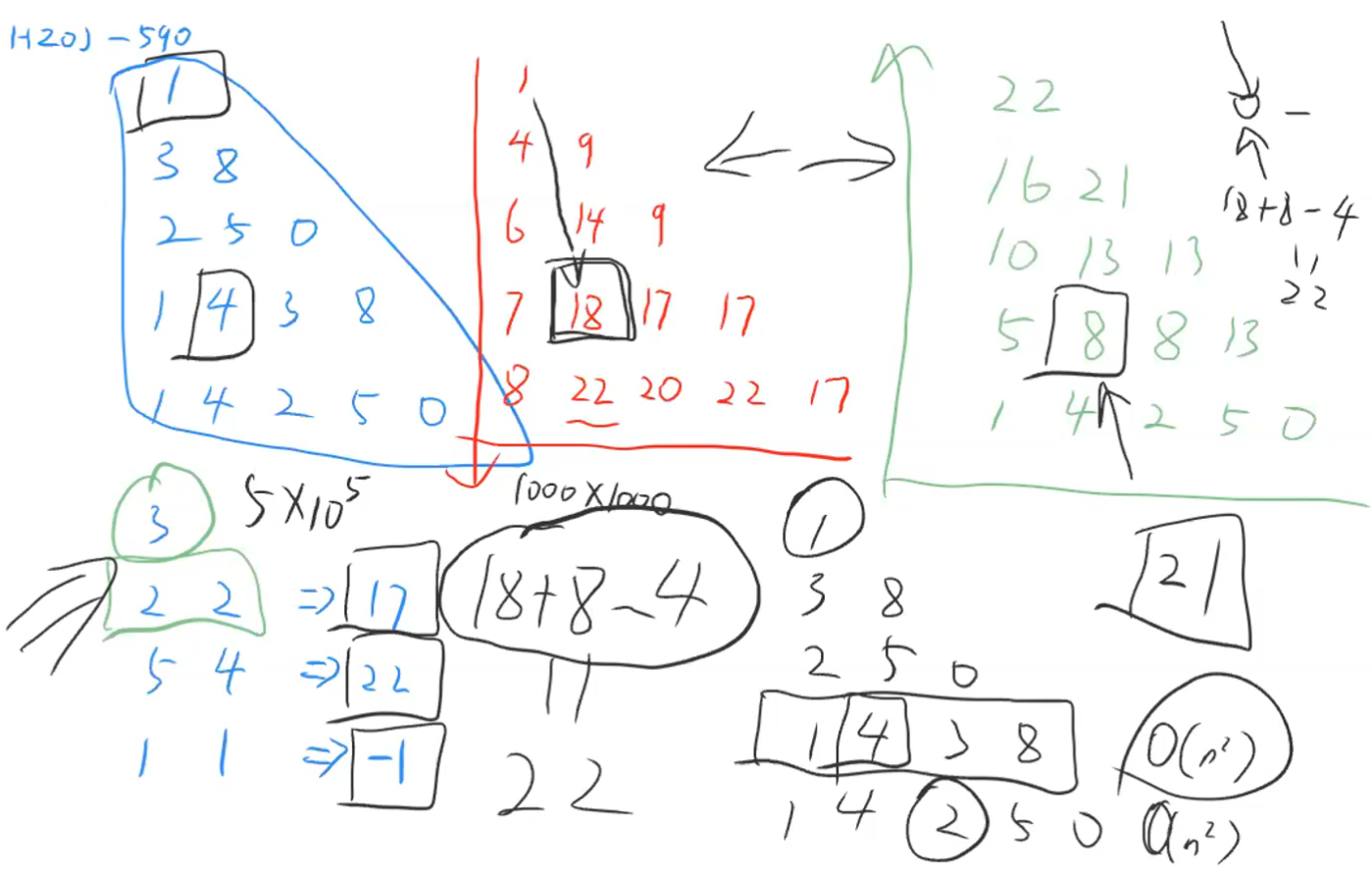
-
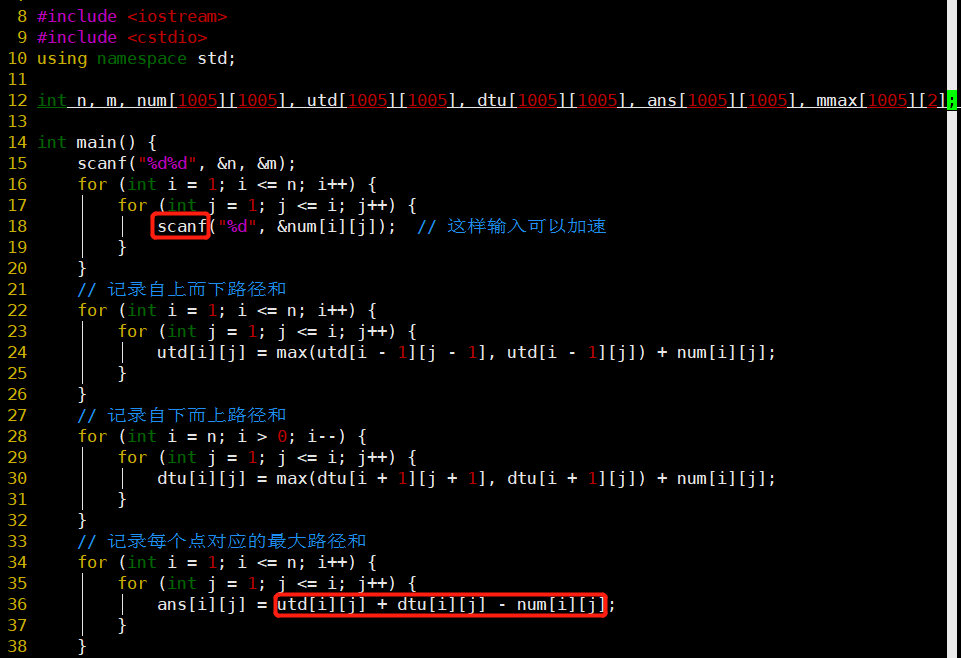
代码
-
-
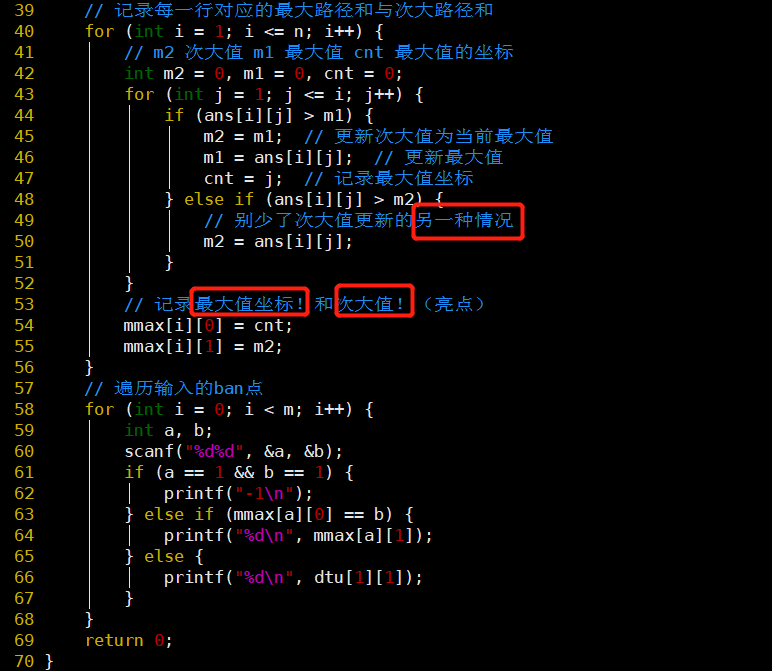
- 找到经过某一点的最大路径和的规律
- 次大值更新的情况要考虑周全
- 记录最大值坐标和次大值即可
- 判断ban掉的是不是最大点或者左上第一个点
- 使用了scanf
- 比cin快,具体见附加知识点2
-
Euler-22:姓名得分
-

-
思路
- 先处理txt文件
- 字母都是大写
- 全局替换","为空格" ",方便数据读入
- 先处理txt文件
:%s /","/ /g
-
- 读入字符串→sort按字典序排序→计算每个姓名的字母值,乘以其排序后的位置,获得得分→累加得分
- 代码
-
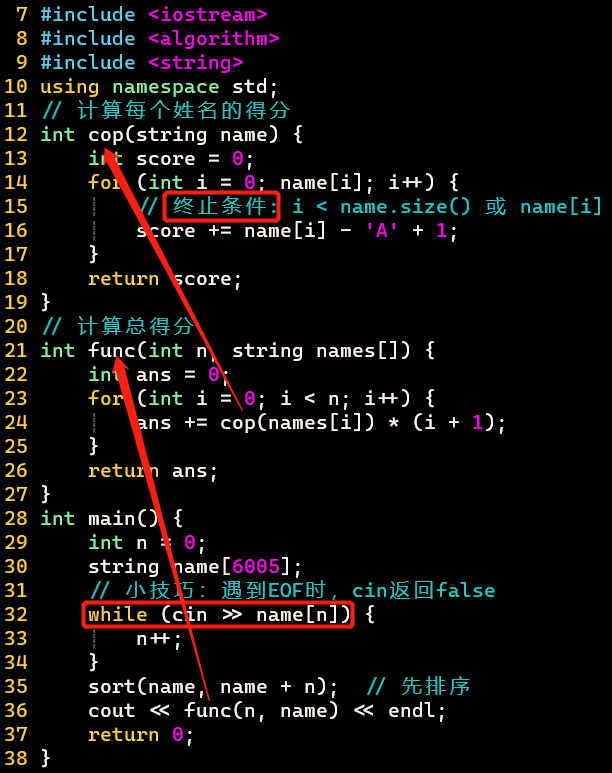
- cin的返回值
- istream&类型
- 大多数情况下其返回值为cin本身(非0值),只有当遇到EOF输入时,返回值为0
- 参考关于C++ cin 的返回值
- string类
- 重载好了小于号,可以直接sort,从小到大排序
- 不支持scanf
- 可以使用.size()获得字符串长度=字符数=字节数
- 终止条件可以使用.size(),也可以使用name[i]判断是不是"\0"
- 两个函数可以直接用两个for循环代替
-
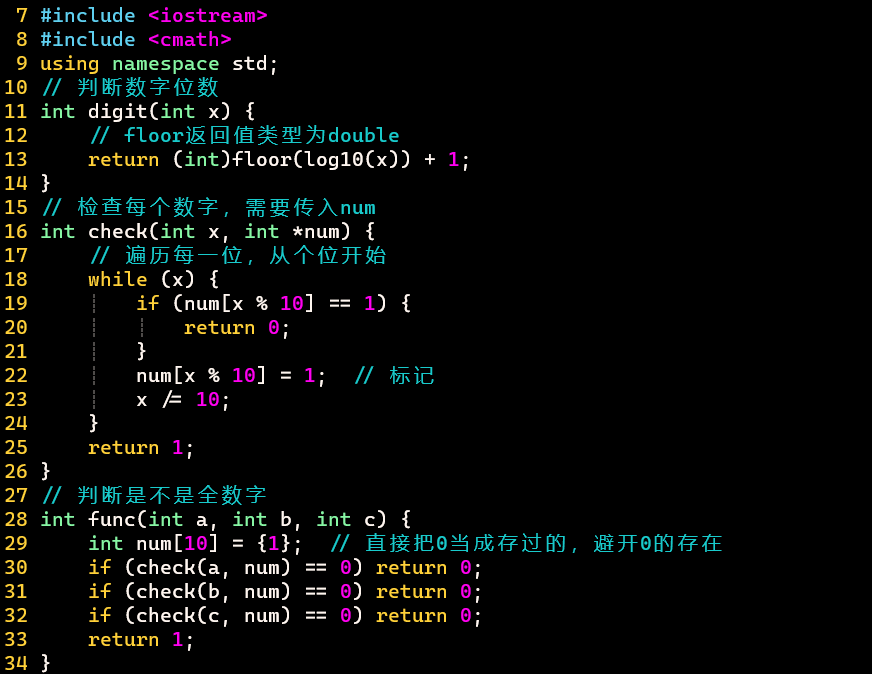
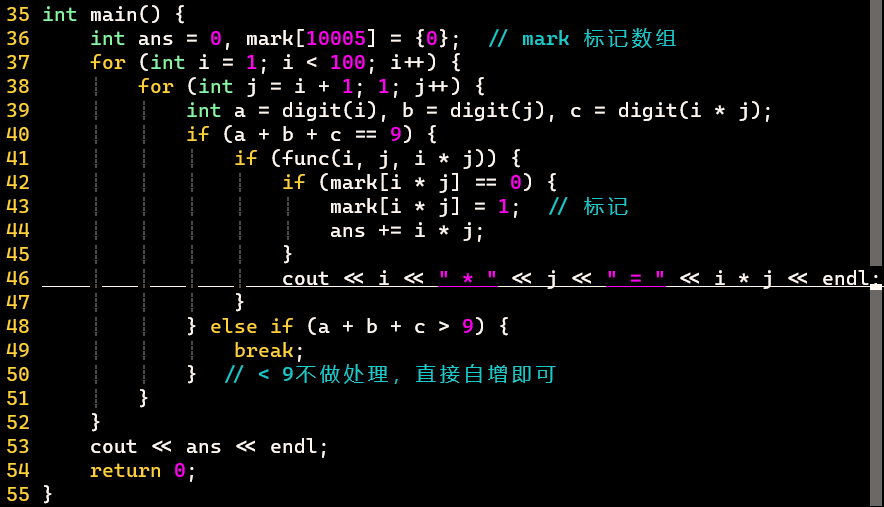
Euler-32:全数字的乘积
-

-
思路
- 全数字概念:xx * xxx = xxxx,存在1~9每个数字一次
- 没有0!
- 避免重复计算
- 第一个数字比第二个数字小
- 第一个数字:范围1~100,当其为100时,第二个数字至少为100,三数位数和超过9
- 第二个数字:停止条件为三个数字位数之和大于9
- 使用log10判断位数:log10下取整+ 1
- 对于正数转int和下取整效果一样,下取整后得到double还需要转int
- 如何判断全数字
- <9不需要判断,只有=9才判断,>9停止
- 使用num[10]存储9个数字的状态
- 乘积可从多个乘法等式中得到,但只求和一次
- 使用标记数组,如果之前存过,就跳过
- 全数字概念:xx * xxx = xxxx,存在1~9每个数字一次
-
代码
-
-
Euler-33:消去数字的分数
-

-
思路
- 有趣
- 有四个非平凡的例子,求四个分数的乘积化为最简分数后的分母值
- 不考虑平凡解,即有0存在,不用考虑太细,可以直接要求每位都不为0
- 分子分母都是两位数,分母比分子大
- 分子:11 - 99;分母:分子 + i
- 四种抹除方式
- 分子1 = 分母1;分子1 = 分母2;分子2 = 分母1;分子2 = 分母2
- 抹除前后判等:十字相乘
-
代码
-
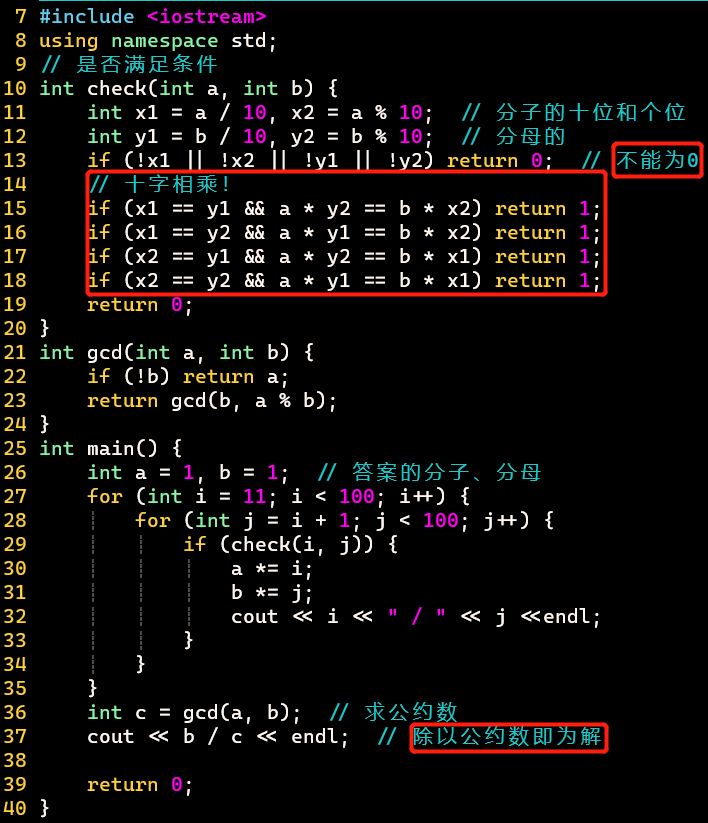
- 十字相乘法判断分数相等
- 通过公约数来得到最简分数
-
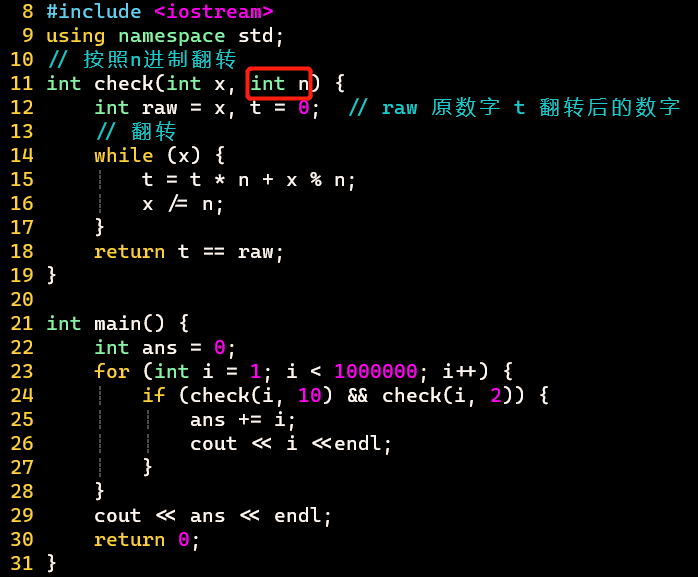
Euler-36:双进制回文数
-

-
思路
- 前导0:如0012332100,不作为回文数
int num;
cin >> num;
// 00123 正常读入为 123
-
- 十进制、二进制都可整合成N进制
-
代码
-
Euler-30:各位数字的五次幂
-

-
思路
- 重点:五次幂之和的最大范围?
设一个X位数
其最大五次幂之和为 9^5 * X
X位数上界为 10^X
估计两个值的交点,即9^5 * X = 10^X,X大约为 5.xxx
所以X最大为 6
-
-
- 枚举10 ~ 1000000
- ⭐提前算好1 ~ 9的五次幂,存起来!
-
-
代码
-
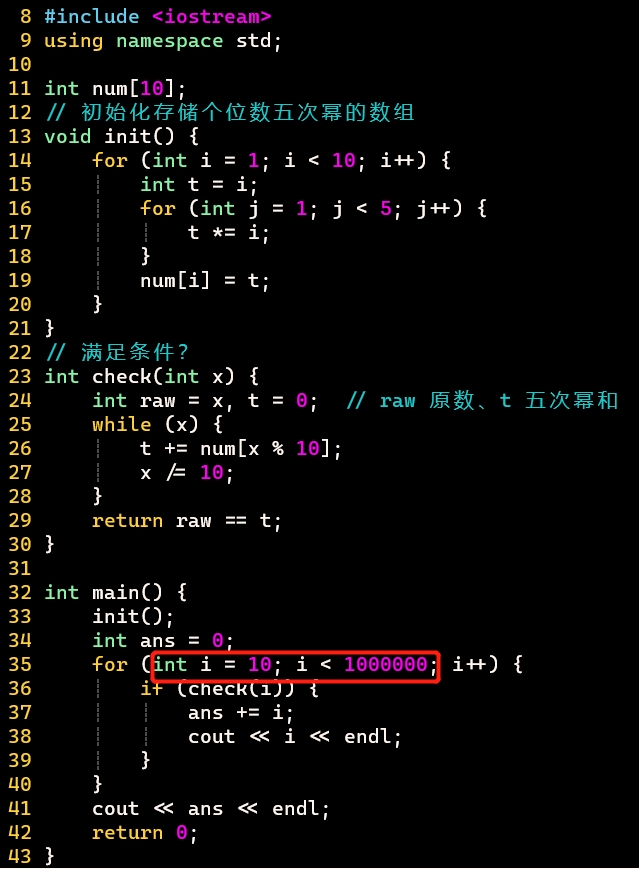
- 关键在于枚举范围!
- 提前存储1 ~ 9五次幂和,避免重复计算
-
Euler-34:各位数字的阶乘
-

-
思路
- 重点:阶乘和的最大范围?
(同上一题)
设一个X位数
其最大阶乘和为 9! * X
X位数上界为 10^X
估计两个值的交点,即9! * X = 10^X,X大约为 6.xxx
所以X最大为 7
-
-
- 枚举10 ~ 10000000
- 同样,⭐提前算好1 ~ 9的阶乘,存起来!
-
- 代码
附加知识点
- 全局变量都会自动初始化为0
- scanf比cin快,参考
- cin、cout的性能可能会很慢,因为它们需要保持与底层C库同步
- 关闭同步会快,但还是不如C的输入输出函数
- 算法竞赛的时候用cin、cout输入输出比用scanf、printf慢多少?-知乎
- 在C++程序中使用scanf()比使用cin更快吗?-腾讯云
- cin、cout的性能可能会很慢,因为它们需要保持与底层C库同步
思考点
-
Tips
-
使用语言为C++,但与C有区别的只涉及到cin、cout
-
time ./a.out 可以显示代码执行时间


