LC-7:整数反转
-

-
思路
- 负数无需额外判断,逻辑一致
- 主要判断(* 10操作)溢出情况,两种方式
- ⭐都很巧妙
- 方式一:用long long存翻转的数字,最后转int判等判断是否溢出
- 方式二:翻转时,每次加一位时判断是否溢出
- 与INT_MAX比:【已大于INT_MAX/10】或者【等于INT_MAX/10且要加的数>7】
- 与INT_MIN比:【已小于INT_MIN/10】或者【等于INT_MIN/10且要加的数<-8】
-
代码
- 方式一:用long long
class Solution {
public:
int reverse(int x) {
// 个人解答
// 不需要考虑负号
long long t = 0;
while (x) {
t = t * 10 + x % 10;
x /= 10;
}
// 判断结果是否在int范围内
return int(t) == t ? t : 0;
}
};
-
- 方式二:加位时判断
class Solution {
public:
int reverse(int x) {
// 官方解答
int rev = 0;
while (x != 0) {
int pop = x % 10; // 每次要加的个位数,提前算用来判断溢出
x /= 10;
// 对应最大值INT_MAX
if (rev > INT_MAX/10 || (rev == INT_MAX / 10 && pop > 7)) return 0;
// 对应最小值INT_MIN
if (rev < INT_MIN/10 || (rev == INT_MIN / 10 && pop < -8)) return 0;
rev = rev * 10 + pop;
}
return rev;
}
}
-
-
- 要加的个位数pop提前算
-
LC-9:回文数
-

-
思路
- 回文数一定不会溢出,因为它就等于它本身
- ⭐翻转一半数字
- 不需要考虑溢出
- 但要记得考虑奇数位的情况!
- 前期可以排除【负数】以及【大于0的以0结尾的数】
- PS:转字符串的方式
- 可以使用C++里的string类,配合to_string()
- 双指针前后判等即可
string str = to_string(x);
- 代码
class Solution {
public:
bool isPalindrome(int x) {
// 【负数】以及【大于0的以0结尾的数】直接出局
if (x < 0 || x % 10 == 0 && x != 0) return false;
int rev = 0;
// 只翻转一半,也不用考虑溢出问题了
while (rev < x) {
rev = rev * 10 + x % 10;
x /= 10;
}
// 注意考虑奇数位情况
return rev == x || rev / 10 == x;
}
};
LC-13:罗马数字转整数
-

-

-
思路
- 涉及加法和减法,用switch...case...即可
- 顺序遍历字符串,对于特殊字符再加一层判断即可
-
代码
class Solution {
public:
int romanToInt(string s) {
int ans = 0;
// 从左到右顺序遍历
for (int i = 0; i < s.size(); i++) {
// 判断情况很多,使用switch...case...
switch (s[i]) {
// 先考虑朴素情况
case 'V' :
ans += 5;
break;
case 'L' :
ans += 50;
break;
case 'D' :
ans += 500;
break;
case 'M' :
ans += 1000;
break;
case 'I' :
// i + 1会不会溢出?不会,字符串末尾有'\0'
if (s[i + 1] == 'V') {
ans += 4;
i++; // 手动多加一次
} else if (s[i + 1] == 'X') {
ans += 9;
i++;
} else {
ans += 1;
}
break; // 记得break
case 'X' :
if (s[i + 1] == 'L') {
ans += 40;
i++;
} else if (s[i + 1] == 'C') {
ans += 90;
i++;
} else {
ans += 10;
}
break;
case 'C' :
if (s[i + 1] == 'D') {
ans += 400;
i++;
} else if (s[i + 1] == 'M') {
ans += 900;
i++;
} else {
ans += 100;
}
break;
}
}
return ans;
}
};
-
- i + 1会不会溢出?不会,字符串末尾有'\0'
LC-14:最长公共前缀
-

-
思路
- 拿此时的公共前缀与下一个字符串比较,更新公共前缀
- 初始公共前缀为第一个字符串
- 中途如果已经为空了,直接返回空
- 直到遍历完所有字符串
- 需有一个变量存储一次比较后的公共前缀
- 拿此时的公共前缀与下一个字符串比较,更新公共前缀
-
代码
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
if (strs.size() == 0) return ""; // 按照惯例,先判断空
string ans = strs[0]; // 答案初始化为第1个字符串
// 从第二个字符串开始遍历
for (int i = 1; i < strs.size(); i++) {
string t = ans; // 存储此时公共前缀 t,不能直接拿ans去遍历!
ans = ""; // 记录一次比较后的公共前缀
// 长度小于【要遍历的字符串长度】和【此时公共前缀】的长度
for (int j = 0; j < strs[i].size() && j < t.size(); j++) {
if (strs[i][j] == t[j]) {
ans += t[j];
} else {
break;
}
}
if (ans == "") {
break;
}
}
return ans;
}
};
-
- 先判断空数组
- 需有新变量存储上次的公共前缀
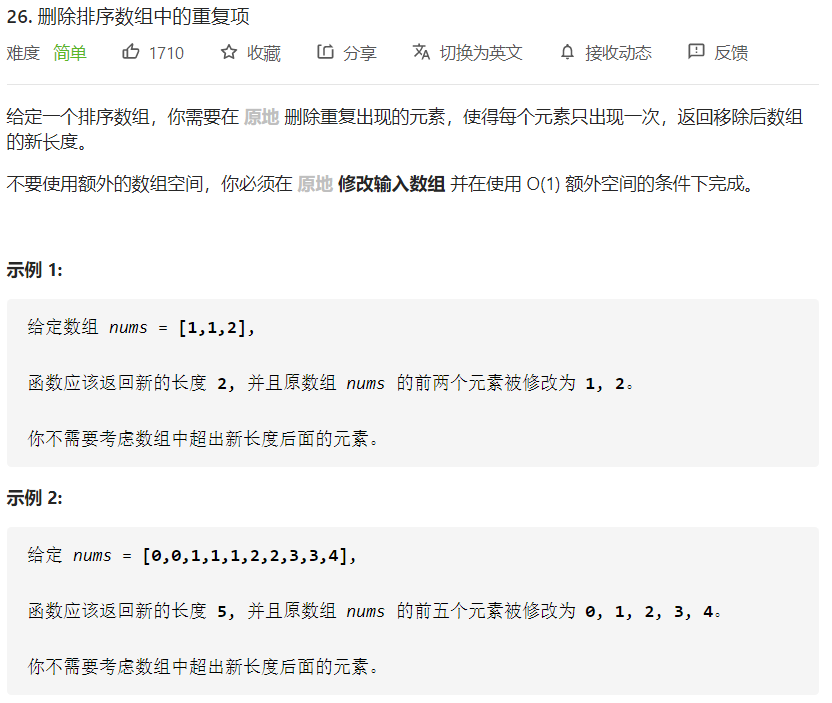
LC-26:删除排序数组中的重复项
-
-

-
思路
- 已排序,原地修改
- 双指针
- 存值的指针+遍历数组的指针
- 两个指针的值
- 不一样,则将值存在前一个指针,并且两个指针一起往后走
- 一样,则只走后一个指针
-
代码
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if (nums.size() == 0) {
return 0;
}
// 存储指针 p、快指针 i
int p = 1; // 第0个数肯定存在
for (int i = 1; i < nums.size(); i++) {
if (nums[i] != nums[i - 1]) {
nums[p] = nums[i];
p++;
// nums[p++] = nums[i];
}
}
return p;
}
};
-
- 双指针~
LC-27:移除元素
-

-
思路
- 与LC-26题类似,甚至更简单
- 同样两个指针
- 相等则快指针往后走
- 不相等则存储指针存值,并且一起往后走
-
代码
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
if (nums.size() == 0) return 0;
int p = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] != val) {
nums[p++] = nums[i]; // 不等于时就存值
}
}
return p;
}
};
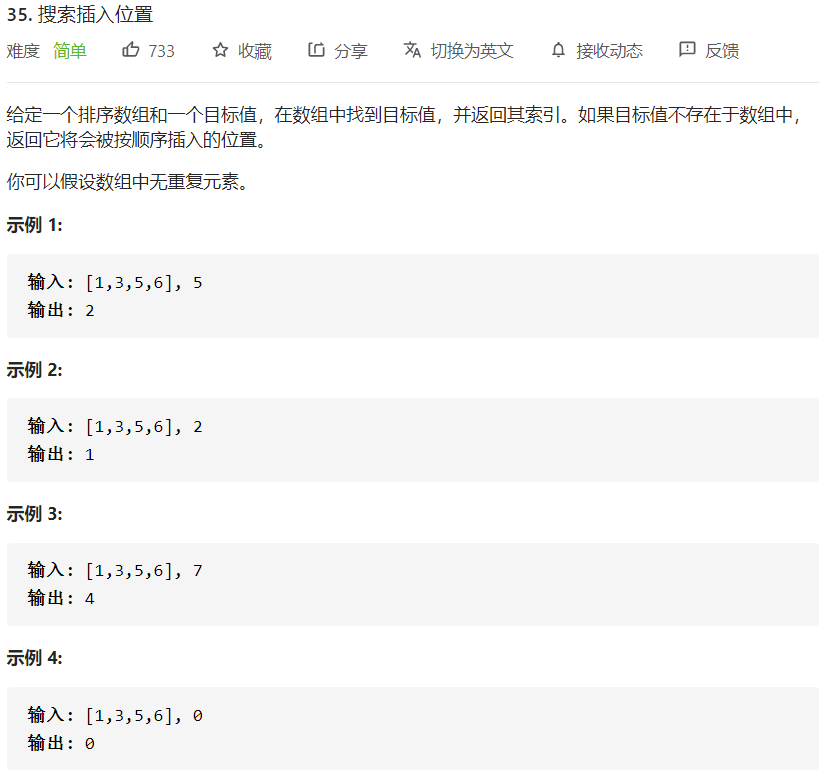
LC-35:搜索插入位置
-
-
思路
- 已排序
- 找到目标值索引,或找按顺序的插入位置
- 0000011111111 特殊二分!
-
代码
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
// 特殊情况:目标值比最大数还大
if (nums[nums.size() - 1] < target) {
return nums.size();
}
// 特殊二分:000001111111
int l = 0, r = nums.size() - 1;
while (l != r) {
int mid = (l + r) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
return r;
}
};
-
- 记得考虑特殊情况:0000000000,提前判断
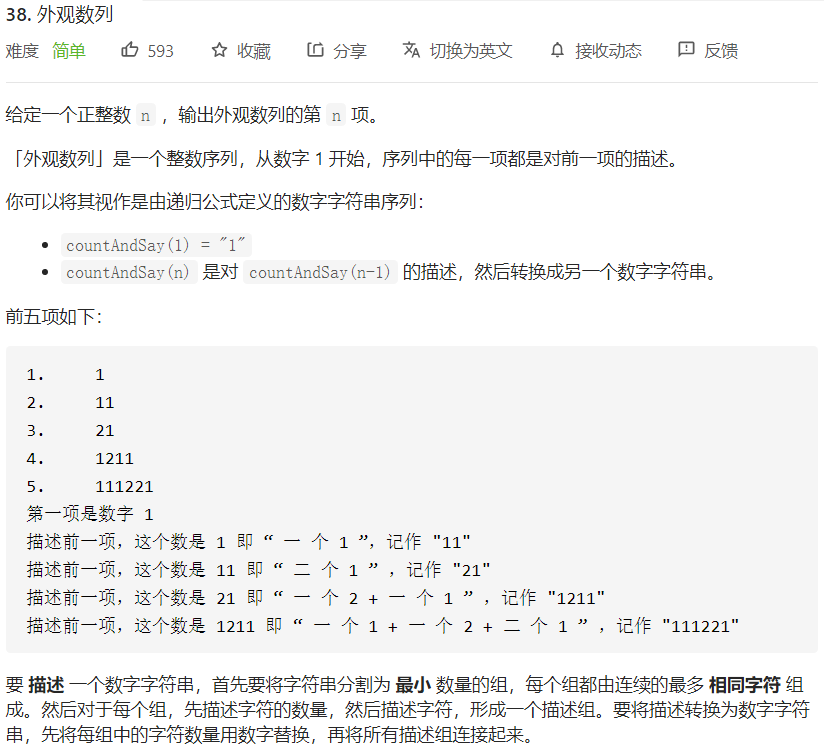
LC-38:外观数列
-
-

-
思路
- 依次根据前一项求后一项
- 计数器计数,初始为1,记得重置为1
- 判断连续了多少个字符,判断前一个和当前字符是否相等
- 依次根据前一项求后一项
-
代码
class Solution {
public:
string ans[5] = {"", "1"}; // 第0项不管,第1项是"1"
// ↑只需要两个字符串交替存储
void func(int s1, int s2) {
ans[s2] = "";
int cnt = 1; // 计数:当前字符连续了多少次
// cnt初始为1,从第二个字符开始
for (int i = 1; i < ans[s1].size(); i++) {
if (ans[s1][i - 1] == ans[s1][i]) {
cnt++;
} else {
ans[s2] += cnt + '0'; // 数字转字符!
ans[s2] += ans[s1][i - 1]; // cnt个什么字符
cnt = 1;
}
}
// 注意:最后一轮还没输出
ans[s2] += cnt + '0';
ans[s2] += ans[s1][ans[s1].size() - 1]; // 最后一个字符
}
void swap(int *a, int *b) {
// 掌握交换的写法
int temp = *a;
*a = *b;
*b = temp;
}
// 题目给的函数
string countAndSay(int n) {
int a = 1, b = 0; // 用来交换字符串编号
for (int i = 2; i <= n; i++) {
func(a, b); // 根据前一个字符串ans[a]求后一个ans[b]
swap(&a, &b);
}
return ans[a];
}
};
-
- 可以使用两个字符串交替记录
- 记得数字转字符
- 注意最后一轮要单独输出
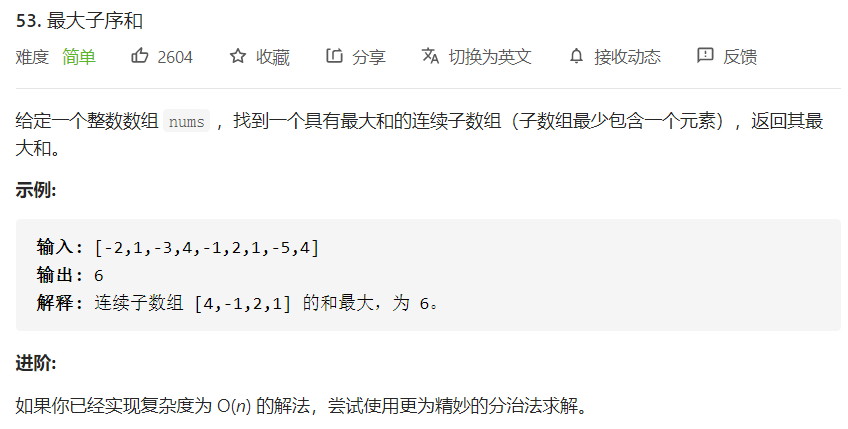
LC-53:最大子序和
-
-
思路
- ans[x] = 以x结尾的最大连续和
- ans[x] = max(ans[x - 1] + num[x], num[x])
- 不需要数组,只需要两个变量
- 上一次最大 ans
- 当前最大 now
-
代码
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int ans = INT_MIN, now = 0; // 也可以直接用nums[0]代替INT_MIN
for (int i = 0; i < nums.size(); i++) {
now = max(now + nums[i], nums[i]); // 关键,当前可达最大值
ans = max(ans, now); // 更新目前最大值
}
return ans;
}
};
-
- 处理好ans和now!
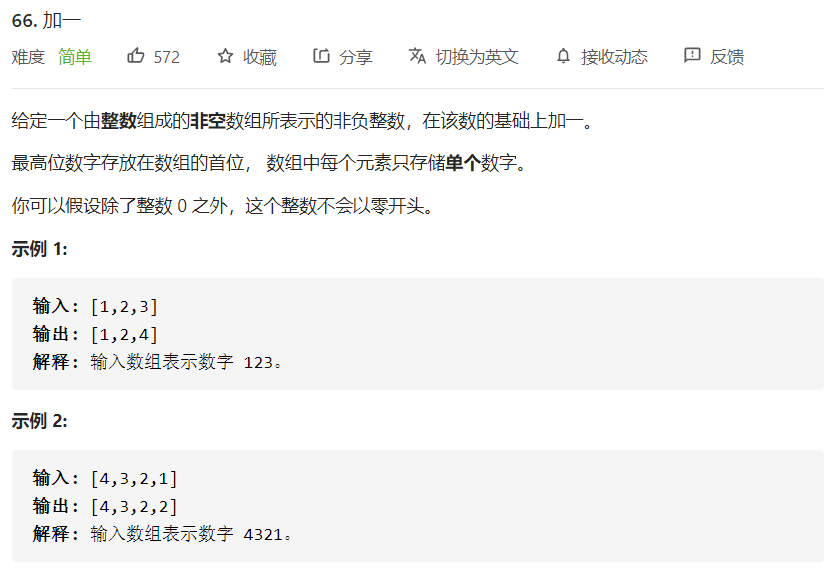
LC-66:加一
-
-
思路
- 比大数加法还要简单,不需要翻转
- 只需要从后往前判断进位情况
- 注意处理最高位进位情况,使用vector的insert方法
- 比大数加法还要简单,不需要翻转
-
代码
class Solution {
public:
vector<int> plusOne(vector<int>& digits) {
digits[digits.size() - 1]++;
// 处理加一后每一位的进位即可
for (int i = digits.size() - 1; i >= 0; i--) {
if (digits[i] == 10) {
digits[i] = 0;
// 特殊处理最高位的进位 else
if (i != 0) {
digits[i - 1]++;
} else {
digits.insert(digits.begin(), 1); // O(N)
// insert、digit.begin()
}
} else {
break;
}
}
return digits;
}
};
-
- insert
- O(N)
- 参考std::vector::insert
- digit.begin()
- 返回一个当前vector容器中起始元素的迭代器
- 参考vector容器 begin()与end()函数、front()与back()的用法-CSDN
- insert
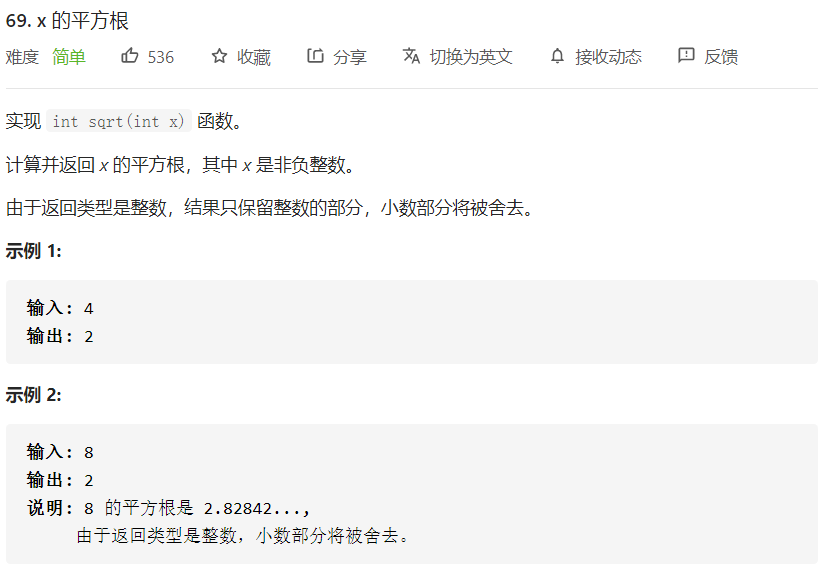
LC-69:x的平方根
-
-
思路
- 整数二分
- 例如:求8的平方根
- 遍历0 - 8:0123456789
- 目标是得到2
- 所以对应1110000000情况
- 整数二分
-
代码
class Solution {
public:
int mySqrt(int x) {
// 111110000
long long l = 0, r = x;
while (l != r) {
// 定义long long
long long mid = (l + r + 1) / 2;
if (mid * mid <= x) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
};
-
- mid * mid可能溢出,所以统一定义long long类型
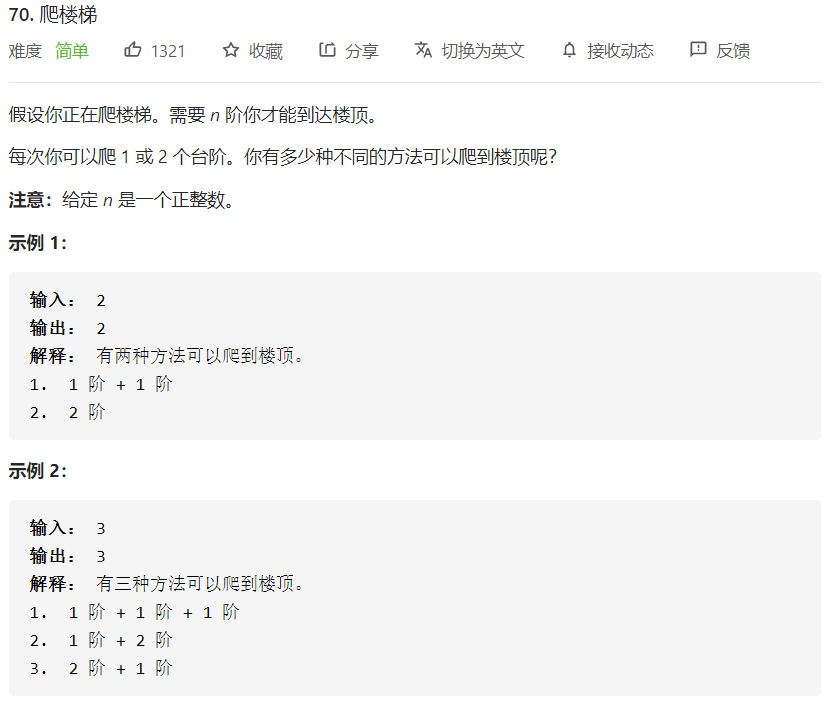
LC-70:爬楼梯
-
-
思路
- 即斐波那契数列
- 两种方式:递归+记忆化;递推
- 延伸:可能有大整数类型的;一次可以爬更多的台阶
-
代码
class Solution {
public:
int ans[50] = {0, 1, 2};
int climbStairs(int n) {
// 函数返回值为int,n=46时,结果会溢出
// 方式一:递归 + 记忆化
if (ans[n]) {
return ans[n];
}
// 记得保存ans[n]
return ans[n] = climbStairs(n - 1) + climbStairs(n - 2);
// 方式二:递推
for (int i = 3; i <= n; i++) {
ans[i] = ans[i - 1] + ans[i - 2];
}
return ans[n];
}
};
-
- 根据题意,函数返回的是int类型,所以n最多到45,n = 46时会溢出
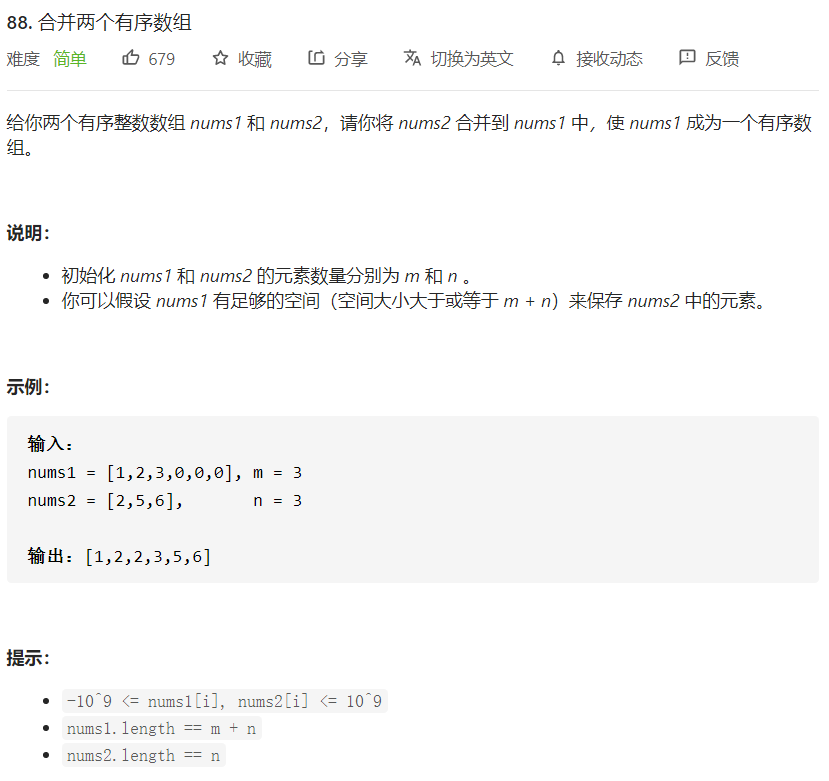
LC-88:合并两个有序数组
-
-
思路
- nums1有足够大的空间,多出来的空间等于nums2的长度
- 从后往前存遍历两个数组,大的从后往前存在num1里
- ❌若从前往后会覆盖,还需处理
-
代码
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
// nums1空间大
for (int i = m + n - 1; i >= 0; i--) {
// 从后往前存
if (m == 0 || n!= 0 && nums2[n - 1] > nums1[m - 1]) {
// nums2元素存进去
nums1[i] = nums2[n - 1];
n--;
} else {
// nums1元素存进去
nums1[i] = nums1[m - 1];
m--;
}
}
}
};
-
- 判断条件要严谨!
- nums2的元素存到后面
- nums1已经遍历完了 ,即m = 0
- 或者
- nums2对应的值大于nums1 并且【nums2还没遍历完!】👈一定要判断
- 即n!= 0 && nums2[n - 1] > nums1[m - 1]
- 否则,nums1的元素存到后面
LC-118:杨辉三角
-

-
思路
- 每位的值等于上左+上的值
- 给出的样本中是用vector实现,不能使用数组的补0大法了!
- 之后注意vector的具体细节
-
代码
class Solution {
public:
vector<vector<int>> generate(int numRows) {
//vector 不能像数组那样留一圈0了,得把每行左右边界提前处理好
vector<vector<int> > ans; // 老标准中<int>后有一个空格
// 特判
if (numRows == 0) {
return ans;
}
// 第一行
ans.push_back({1});
// 第二行对应i = 1
for (int i = 1; i < numRows; i++) {
vector<int> v; // 先定义一个临时的vector存这一行
v.push_back(1); // 左边界
// 第i行除了两端的1还有i - 1个元素
for (int j = 1; j < i; j++) {
v.push_back(ans[i - 1][j - 1] +ans[i - 1][j]);
}
v.push_back(1); // 右边界
ans.push_back(v);
}
return ans;
}
};
-
- vector的方法:push_back
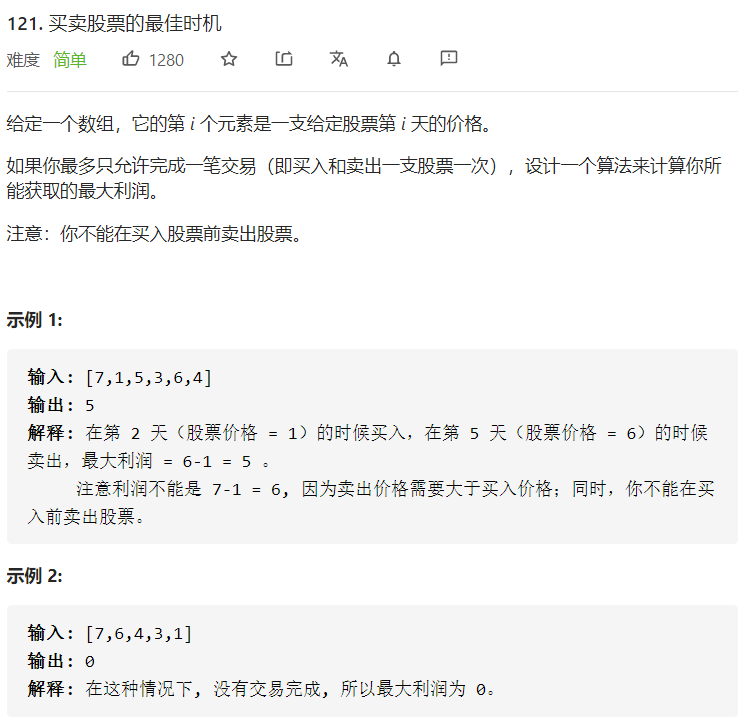
LC-121:买卖股票的最佳时机Ⅰ
-
-
思路
-
只买卖一次
- 遍历
- 更新当前最小值:先初始为第一个数
- 更新答案:【临时答案】与【当前值-当前最小值】作比较
- 答案初始为0
- 输出答案
- 遍历
-
代码
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) {
// 需要特判,否则下面初始化时的prices[0]不存在会报错
return 0;
}
int ans = 0, mmin = prices[0];
for (int i = 1; i < prices.size(); i++) {
ans = max(ans, prices[i] - mmin);
mmin = min(mmin, prices[i]);
}
return ans;
}
};
-
- 答案ans初始为0,当前最小值mmin初始为第一个数prices[0]
- 用两个m是为了避免与C++的min()函数重名
- 需要特判,prices里可能没有值
- vector.size()
- 答案ans初始为0,当前最小值mmin初始为第一个数prices[0]
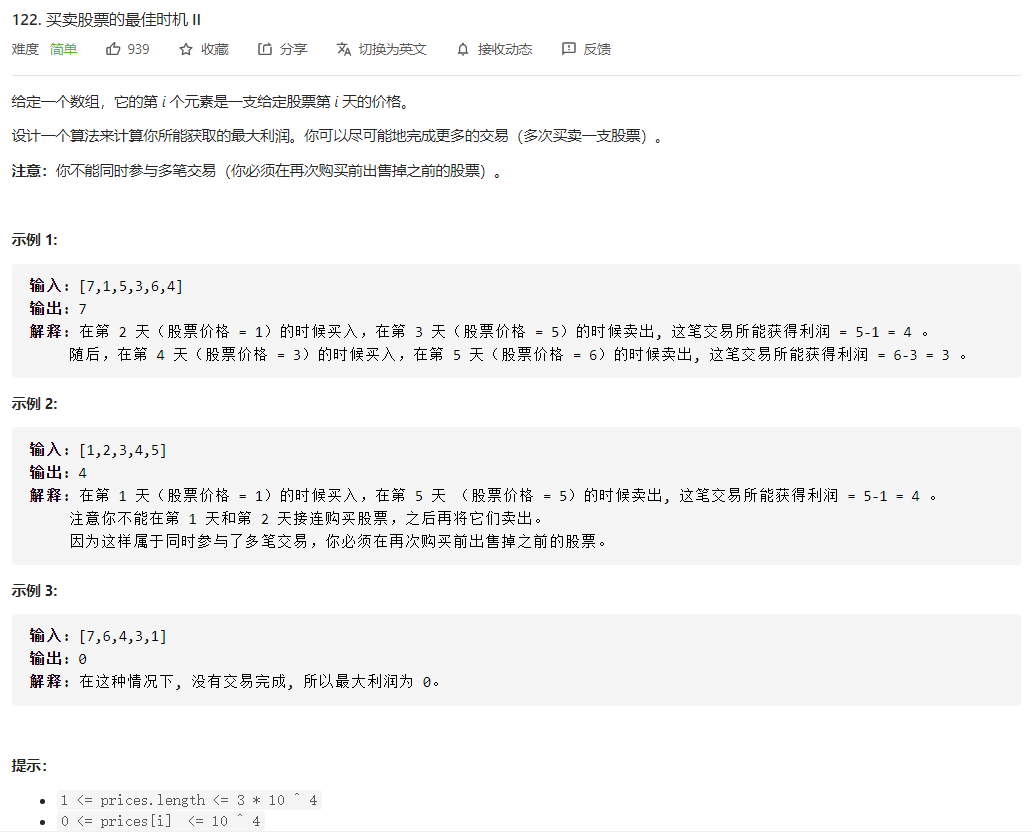
LC-122:买卖股票的最佳时机Ⅱ
-
-
思路
- 可以买卖任意次
- 两天两天地考虑,只看相邻两天能否赚
-
代码
class Solution {
public:
int maxProfit(vector<int>& prices) {
// 分成数个两天
// 可加特判
int ans = 0;
for (int i = 1; i < prices.size(); i++) {
// 只要当前这天比前一天股价高
if (prices[i] > prices[i - 1]) {
ans += prices[i] - prices[i - 1];
}
}
return ans;
}
};
-
- 特判可加可不加,因为prices.size()已经限制了循环
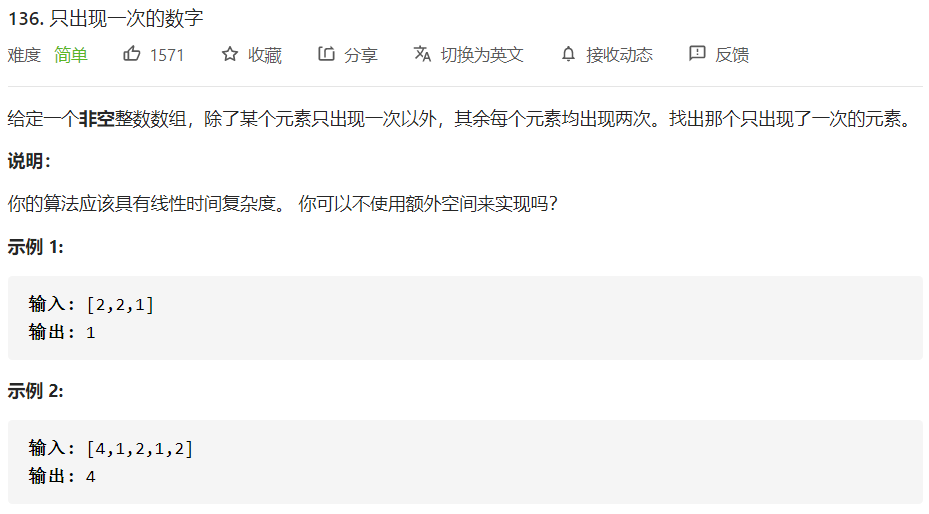
LC-136:只出现一次的数字
-
-
思路
- 精髓:按位异或
- 0 ^ x = x
- x ^ x = 0
- 精髓:按位异或
-
代码
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ans = 0;
for (int i = 0; i < nums.size(); i++) {
ans ^= nums[i];
}
return ans;
}
};
附加知识点
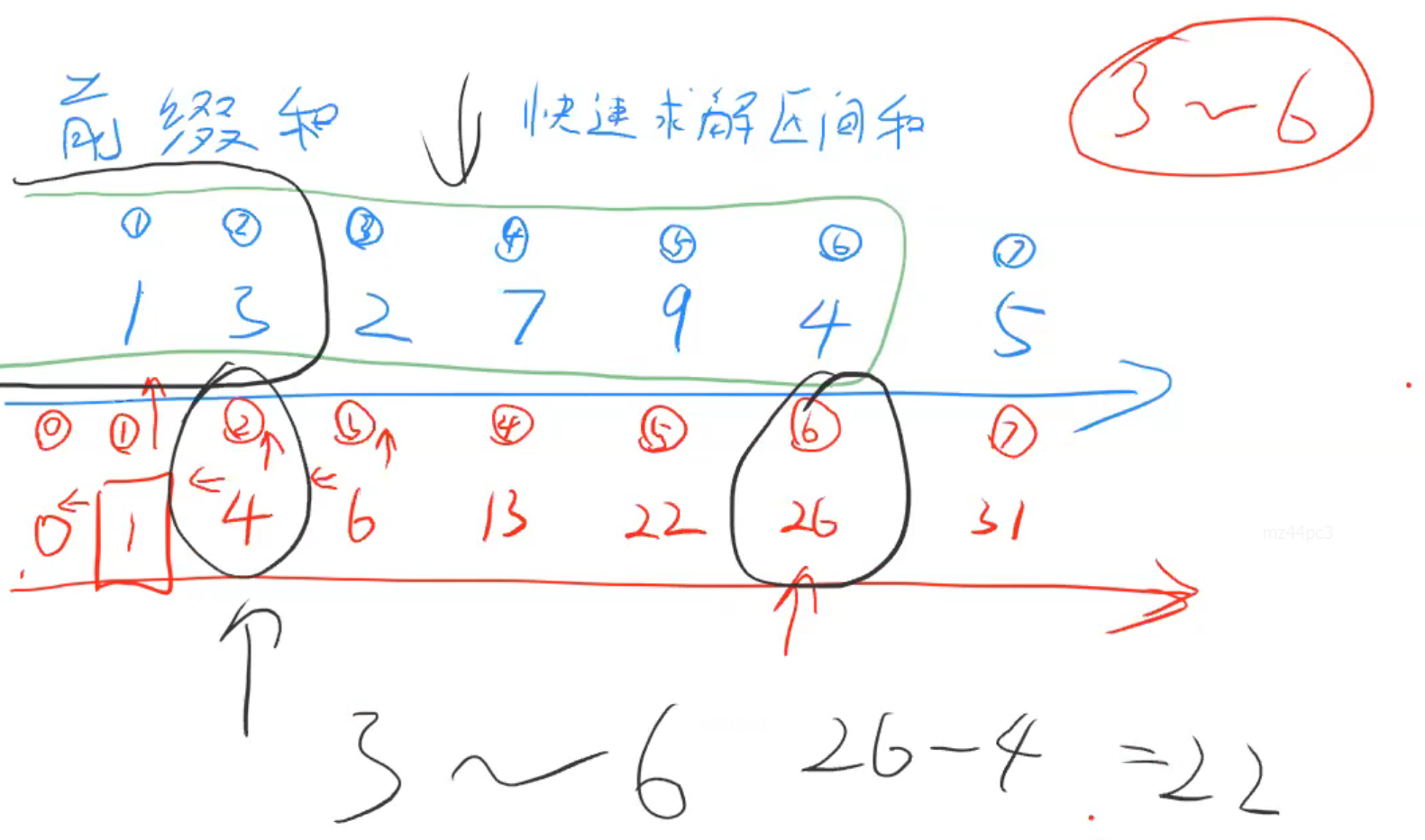
前缀和
-
-
快速求解区间和
- 前缀和数组sum
- 区间[x, y]的和:sum[y] - sum[x - 1]
- 数组多开一个0位,避免①对应的sum[1 - 1]无值
-
维护额外的数组,避免多次询问的耗时
思考点
Tips
课程速记
- 自做:67、119(参考118)、125


