——递归热身——
HZOJ-240:图形打印4

样例输入
1
2
3
4
-1
样例输出
X
-
X X
X
X X
-
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
-
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X
X
X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X
X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
-
- 思路
- 递归
- func(x, x, n):从点(x, x)开始,画大小为n的图形
- 边界:当n = 1时,在点(1, 1),画'x'
- 分解:func(x, x, n)由5个有排列规律的func(x', x', n - 1)组成
- ⭐根据边长预测5个部分的起始点的位置
- 边长L是首项为1,公比为3的等比数列
- 以左上角点为基准:其余3个顶点的偏移量是L / 3 * 2、中心点的偏移量是L / 3
- ⭐根据边长预测5个部分的起始点的位置
- 需要输出多次,而n最大为7
- 所以,直接存好func(1, 1, 7)的结果,根据输入n输出即可
- 代码
-

- 先存好图形数组,5个部分的起始点位置
-
——排列组合——
- 排列组合三兄弟:指数型、组合、全排列
- 延伸
- 【组合问题】对于1个数组num[100],任选5个数,输出和
- 【全排列问题】对于1个数组num[100],输出全排列
- 【组合+全排列】n个数任选m个数,再对m个数全排列,即236 + 237组合练习
- 先组合,再对得到的组合数进行全排列
- 【3兄弟自由组合】
- 延伸
- 时间复杂度都很高
- 全排列:O(n!)
HZOJ-235:递归实现指数型枚举

样例输入
3
样例输出
1
1 2
1 2 3
1 3
2
2 3
3
- 思路
- 按字典序排序
- 递归的每一层选一个数字
- 第1层:在1 ~ n中选
- 若某一层选出 i,则下一层:在 i + 1 ~ n中选。注意:直接+1!
- 举例:n = 4
第一层:1 2 3 4中选→1
第二层:2 3 4中选→2
第三层:3 4中选→3
第四层:4中选→4
- 代码
- 第一版:func函数用2个参数,便于理解→从几开始选+这是第几层
-
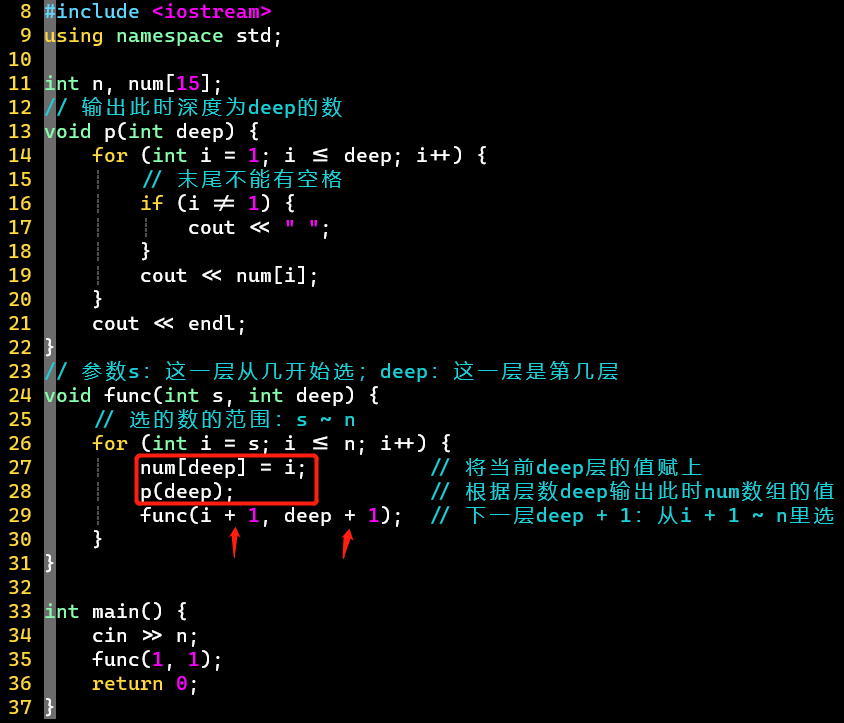
- 用num[15]存前面已经存好的数,最多10个数
- 第二版:func函数用1个参数,更有回溯感→从几开始选【把这是第几层放到全局里】
-
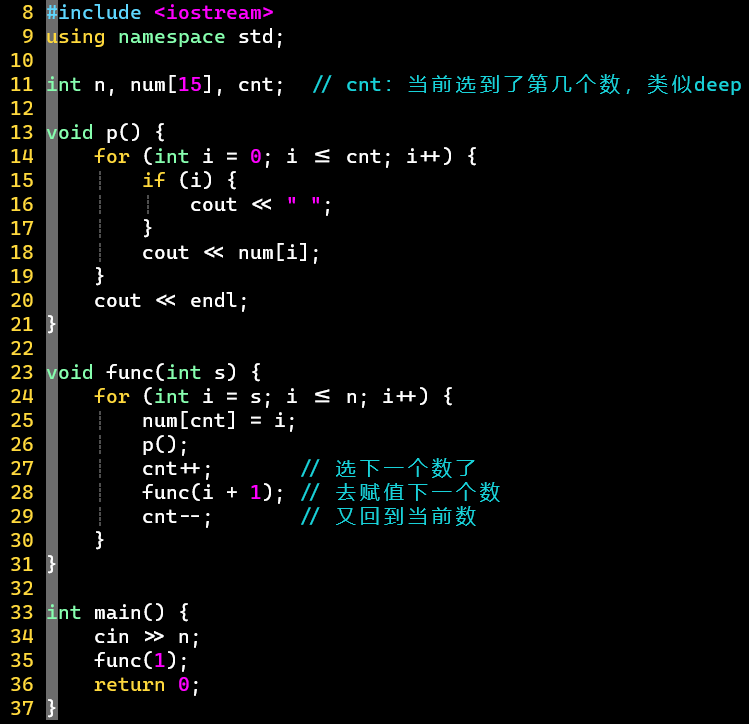
- 注意:与版本一不同,这里的深度cnt是从0开始,版本一的deep是从1开始
- 深度从1还是0取决于自己,但自己在存值和输出时要统一
HZOJ-236:递归实现组合型枚举
样例输入
5 3
样例输出
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
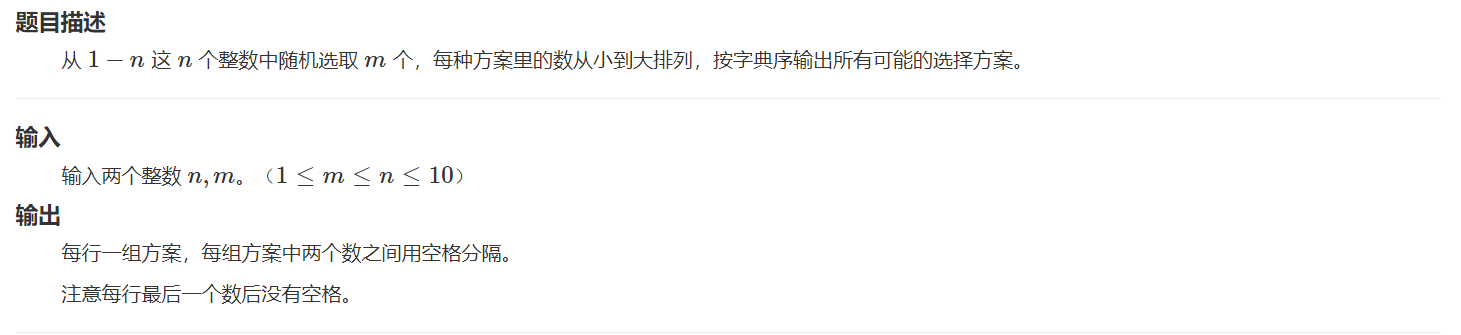
- 思路
- 类似上一题[指数型枚举],直接修改的话:增加输出条件,存了m个数才输出
- 同样可用2个或3个参数:多一个输出条件,存的深度达到m才输出
- 2个更有回溯感;3个更易理解
- 代码
- func函数用2个参数版
-
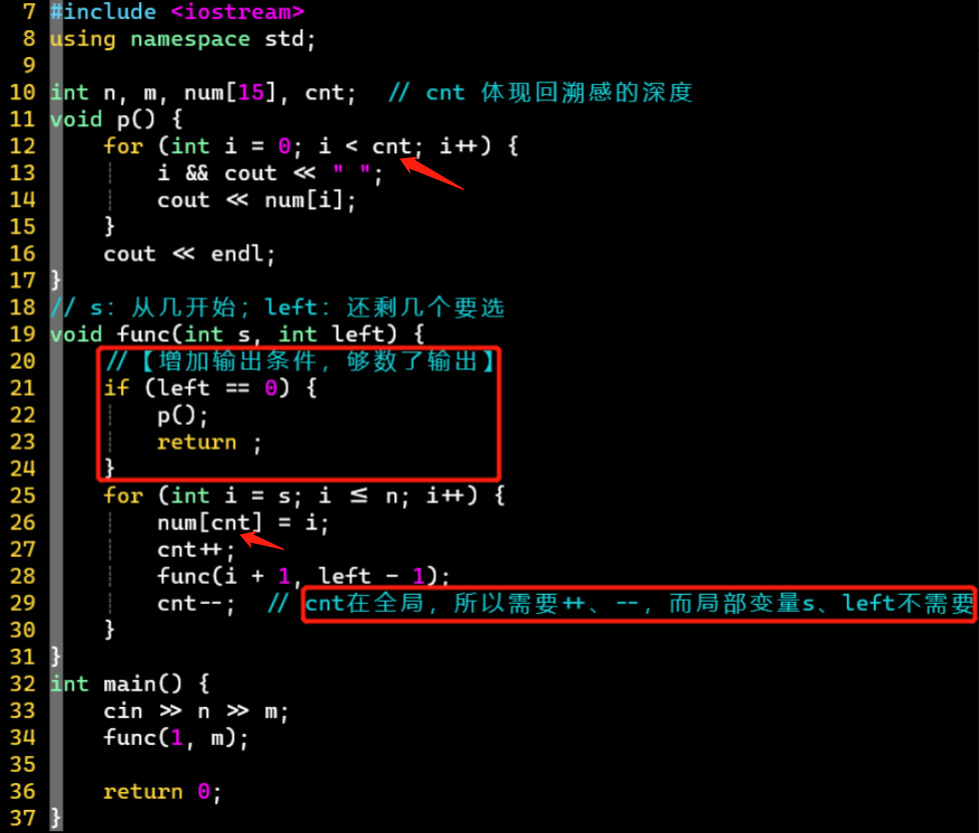
- 可自己手写体会
- 【经测试】实际上变量cnt或left中的一个可以不需要
- 不要left:第12行,cnt可由m代替;第26行,cnt可由m - left代替;清除其他cnt
- 但用cnt理解更清晰
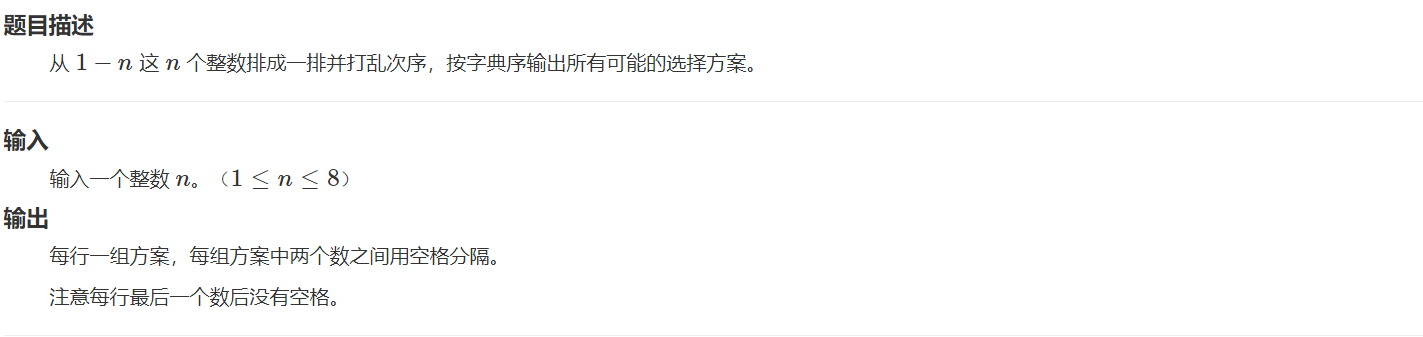
HZOJ-237:递归实现排列型枚举
样例输入
3
样例输出
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
- 思路
- 全排列
- 每一层都是1~n:这一层与上一层没关系
- 引入mark数组:标记已经选了哪些数了
- C++里自带全排列函数next_permutation、prev_permutation
- 参考STL中的全排列函数
- 但其实不是很好用,自己实现更灵活
- 全排列
- 代码
-
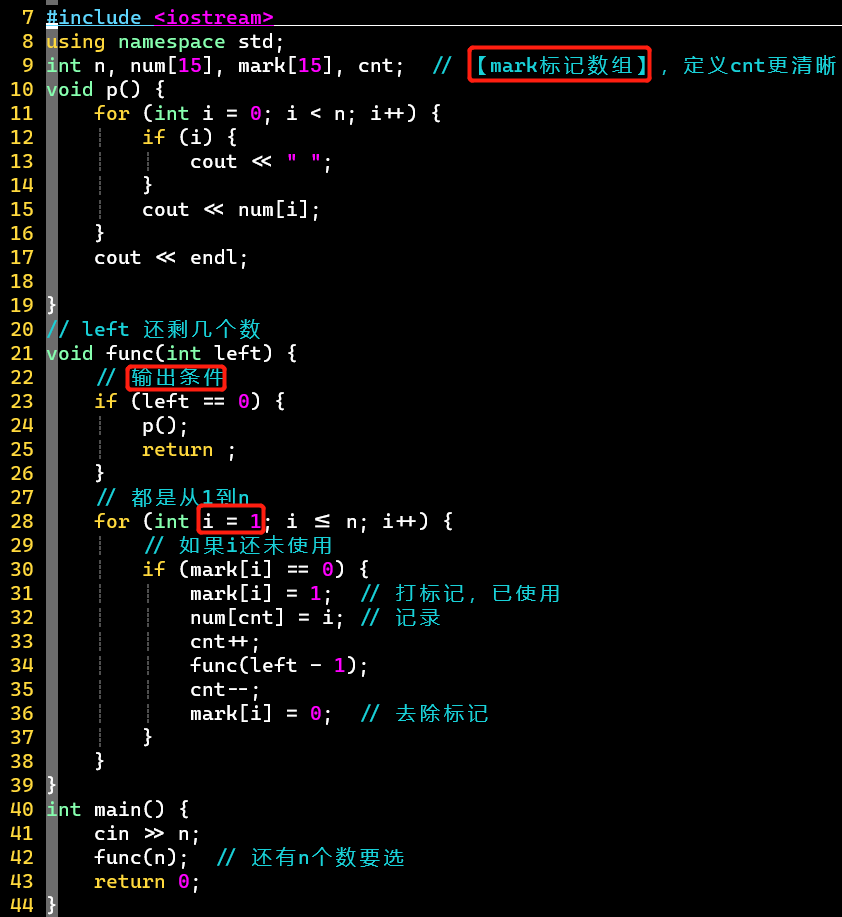
- 添加标记数组,打标记操作和cnt加减操作的配合
-
——深搜——
- 接上:递归👉排列组合👉搜索(深搜)
- 排列组合其实是深搜的一种
- 联想树的遍历
- 往下搜:cnt++;往上回:cnt--
- ⭐主要解决【连通性】问题
- 两个点是否相连,相连的点有哪些、有多少
- 解决最短路径问题很费劲,需要遍历所有路径,可以找但没必要
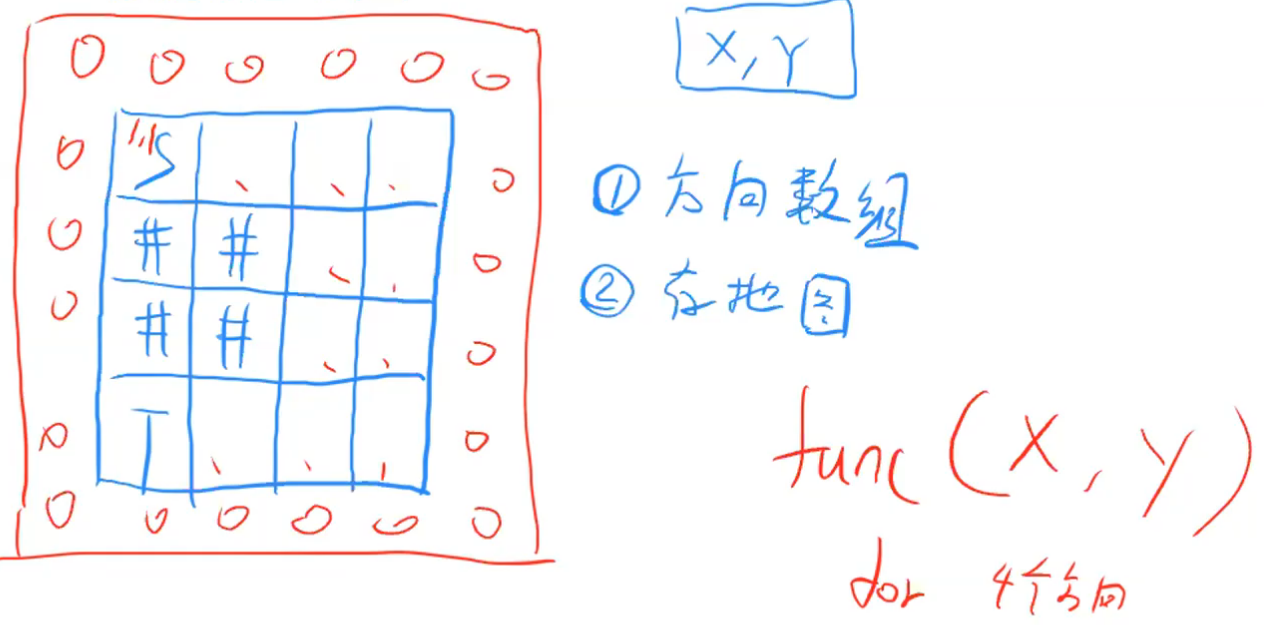
深搜走地图——基本模板
- 方向数组:根据当前所在点可以得到下一点的位置,判断是否可走、到达终点
- 存地图:补0,可以减少边界判断,如果用vector需要手动判断边界
- 递归、去重 [或标记数组]、补0 [或判断边界]
代码
-

-
每次拿到新的点,就以新的点为起点再搜 [递归]
-
走到终点会提前停止搜索,走不到的情况会把所有路径都枚举一遍
HZOJ-535:瓷砖

样例输入
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
样例输出
59
- 思路
- 深搜、走到底;广搜也能做
- 注意:输入h、w的顺序
- 样例为9行11列,输入为11 9
- 能走多少个'.',用一个答案ans存,起始为1
- 代码
-

- 不需要返回值,统计全局变量ans即可
-
HZOJ-397:僵尸来袭

样例输入
5 6
0 1 2 3 4 0
1 0 0 0 0 0
2 9 3 0 2 4
0 0 2 0 2 8
1 0 0 0 0 0
样例输出
4
- 思路
- 遍历,找到一个非0,波数+1,并以其为起点,【深搜】清除和它一波的僵尸
- 每经过一个非0,就置为0,避免之后的重复搜索
- 再下一波
- 非0值的数值大小在这里没有用,只管0/非0
- 遍历,找到一个非0,波数+1,并以其为起点,【深搜】清除和它一波的僵尸
- 代码
-
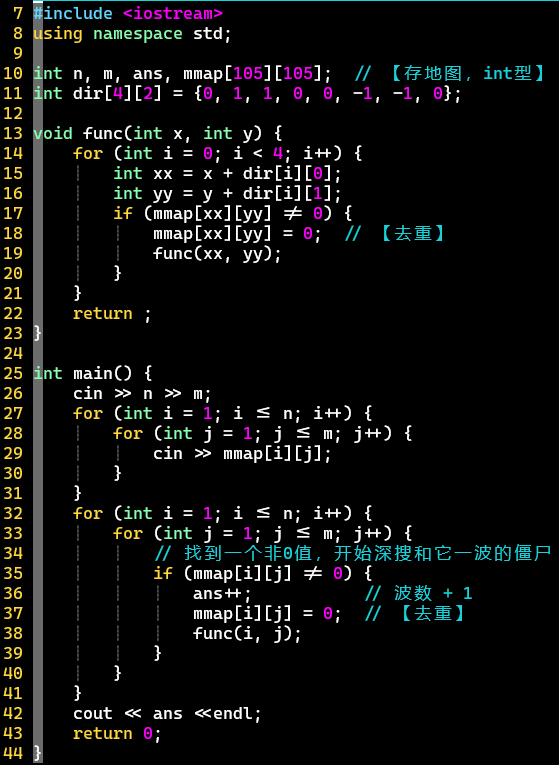
- 连通性问题,注意去重、输入地图为int型
-
HZOJ-536:最大黑色区域

样例输入
5 6
011001
110101
010010
000111
101110
样例输出
7
- 思路
- 上题为有几片黑色区域,这题为最大的黑色区域有多大
- 记录临时最大值即可
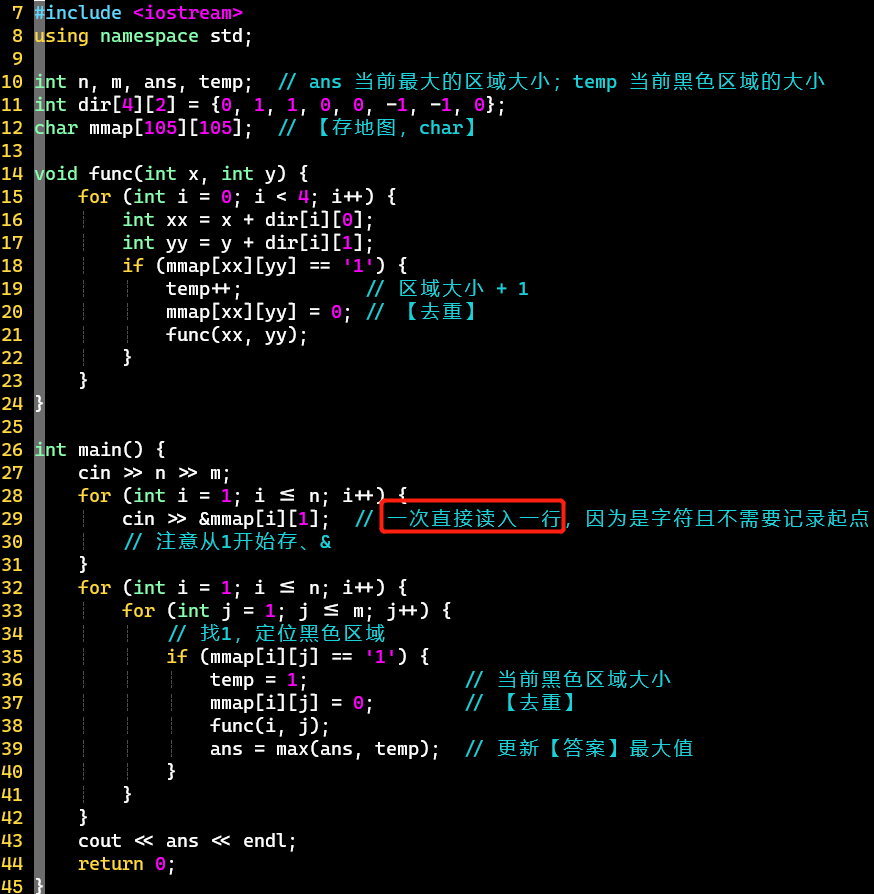
- 注意
- 输入的矩阵是字符,可以一次读入一行:cin >> &mmap[i][1];
- 去重
- 代码
-
HZOJ-396:填涂颜色⭐

样例输入
6
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 0 0 1
1 1 0 0 0 1
1 0 0 0 0 1
1 1 1 1 1 1
样例输出
0 0 0 0 0 0
0 0 1 1 1 1
0 1 1 2 2 1
1 1 2 2 2 1
1 2 2 2 2 1
1 1 1 1 1 1
- 思路
- 只有0、1
- 被1包住的0没法判断,但【没被1包住的0】可以判断!
- ❗ 没被1包住的0肯定与边界相连
- 把没被包住的0改成其他值:3
- 【输出只管】遇到3输出0,遇到0输出2
- 如何找没被1包住的0呢?
- ❌方法一:遍历整个外圈,遇到0就深搜
-

- 【麻烦】0有可能被1分割,有多片区域,所以要遍历整个外圈
-
- ⭐方法二:补0,找和左上角点[0, 0]点联通的0
-

- 【妙】这些0和没被1包住的0全是连通的,可以一次搜索处理掉!
- 注意:必须严格判断边界
-
- ❌方法一:遍历整个外圈,遇到0就深搜
- 代码
-
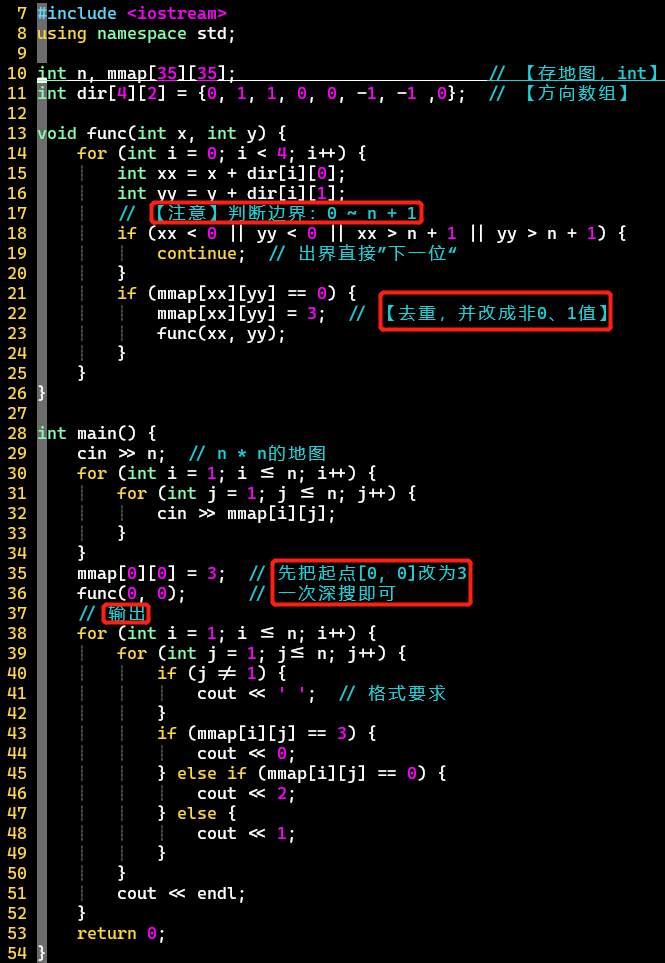
- 注意判断边界、输出判断
-
HZOJ-404:01迷宫简易版

样例输入
2 3
011
100
2 3
样例输出
2
- 思路
- 深搜,相当于求最大连通域
- 移动方式为:0→1,1→0。即不相同才能移动
- ⭐引入标记数组
- 【去重】该场景使用标记数组更方便,减少判断次数
- 【不能补0】0在本题有特殊用途,需额外判断边界
- 代码
-
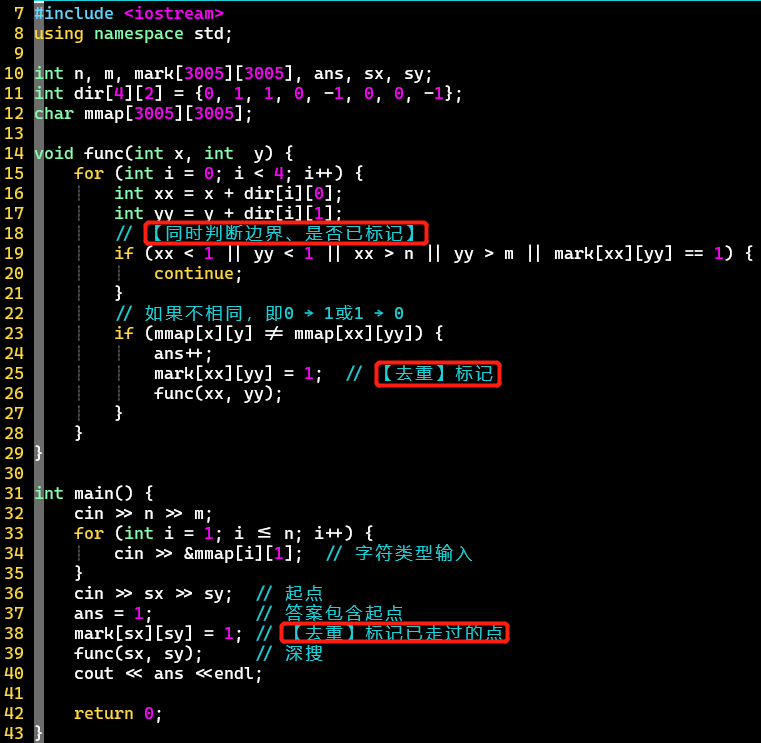
- 标记数组的引入!
- 需要判断边界,因为搜索条件为不相同时继续
- 虽然这里像是补了0,其实没用到
-
HZOJ-405:01迷宫⭐

样例输入
2 3 4
011
100
1 1
2 2
1 3
2 3
样例输出
4
4
2
2
- 思路
- 深搜
- 与上题的区别:询问次数很多!高达30000次
- 如果用上题方式,每来一个坐标求一次,必超时
- 👇空间【答案数组】换时间👇
- 需要额外的数组存每个点的答案:ans[3005][3005]
- ⭐此外,需要用队列[方便,栈、数组都行]存某个连通区域的点集合
- 只有搜索完这一个连通域才知道它们的答案 [相同的]
- 代码
-
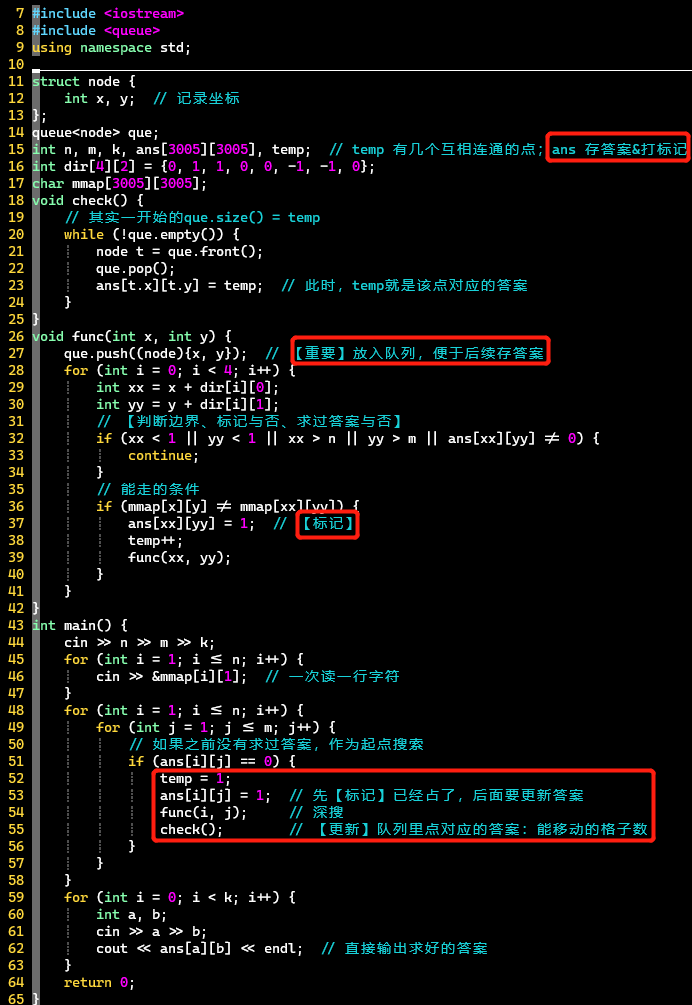
- ❗ 答案数组兼任标记数组去重
- 这里,补0没有作用,只是习惯从1开始读了
- 队列的size()其实也是当前的答案temp
- 输出,直接输出答案数组对应坐标的值即可
-
——广搜——
-
同样可解决【连通性】问题。如HZOJ-396:填涂颜色,思路见上
-
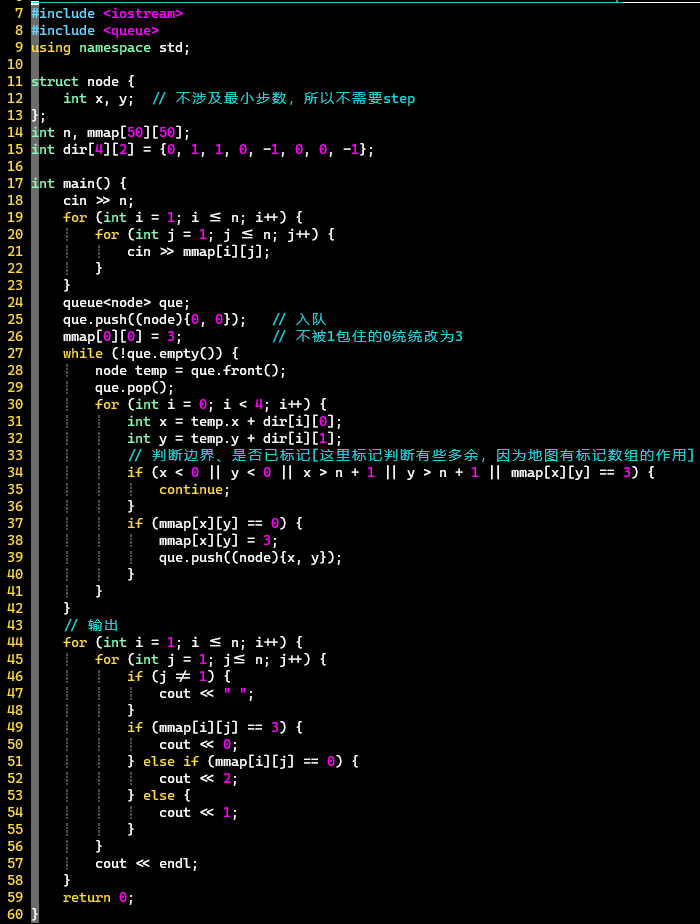
-
除了可以解决【连通性】问题外,还可以解决⭐【最短路径】问题
- 从起点到终点最少需要多少步
- 最先搜到的点一定是最短的,因为是按层来的→层序遍历
广搜走地图——基本模板
- 方向数组、存地图
- 队列[必须]:存遍历的点,而不需要递归;其元素为自定义结构,存坐标、当前步数
- 去重 [或标记数组]、补0 [或判断边界]
代码
-
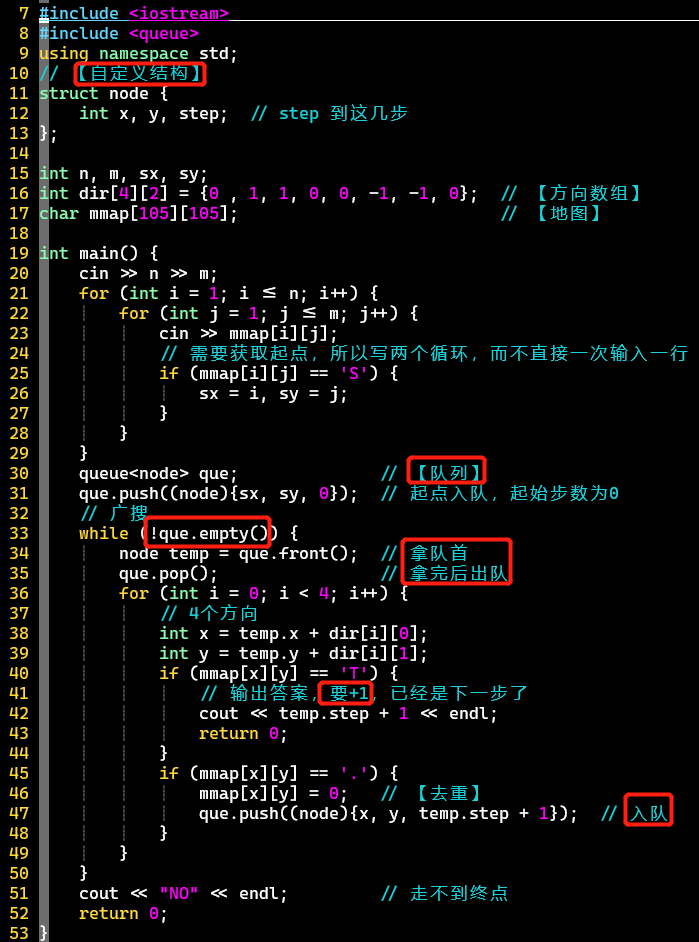
-
关键:入队出队、自定义结构体
HZOJ-399:小明吃饭

样例输入
5 6
2.....
###.#.
....#.
..###.
....3.
样例输出
10
- 思路
- 即广搜走地图——基本模板
- 代码
-
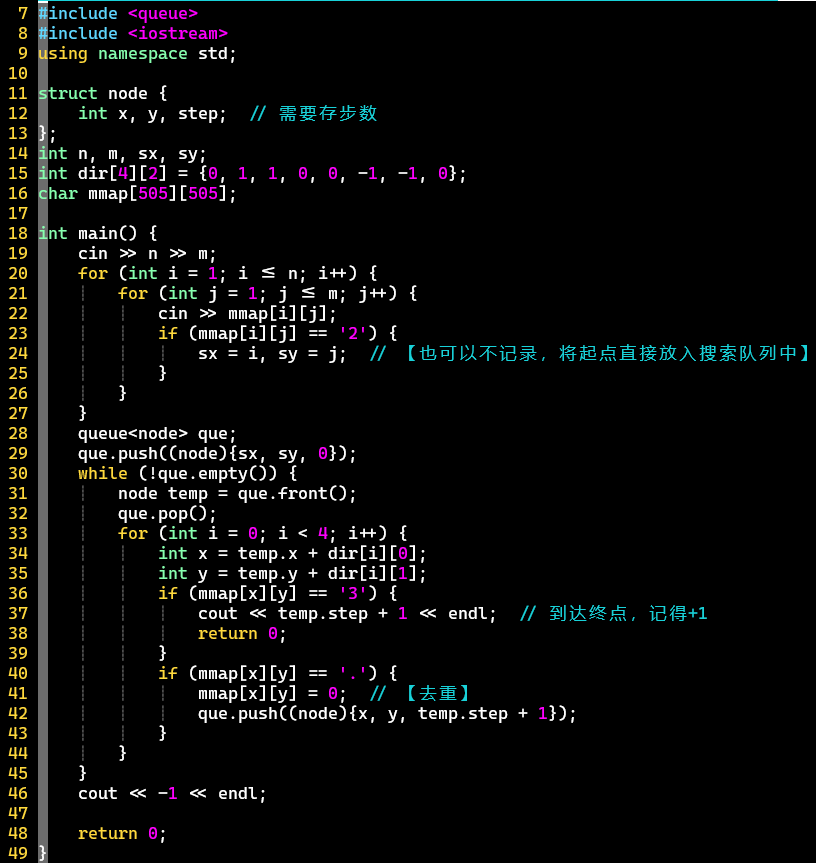
- 去重:改成非可走的字符'.'即可,如0
-
HZOJ-304:骑士风度的牛

样例输入
10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..
样例输出
5
- 思路
- 像马的走法
- 方向数组变成8个
- [1, 2] 和 [2, 1]组合各四种
- 没有憋腿的情况
- 注意越界问题:从1, 1点存还要判断边界,直接从2, 2点存
- 坑:先输入列数
- 代码
-
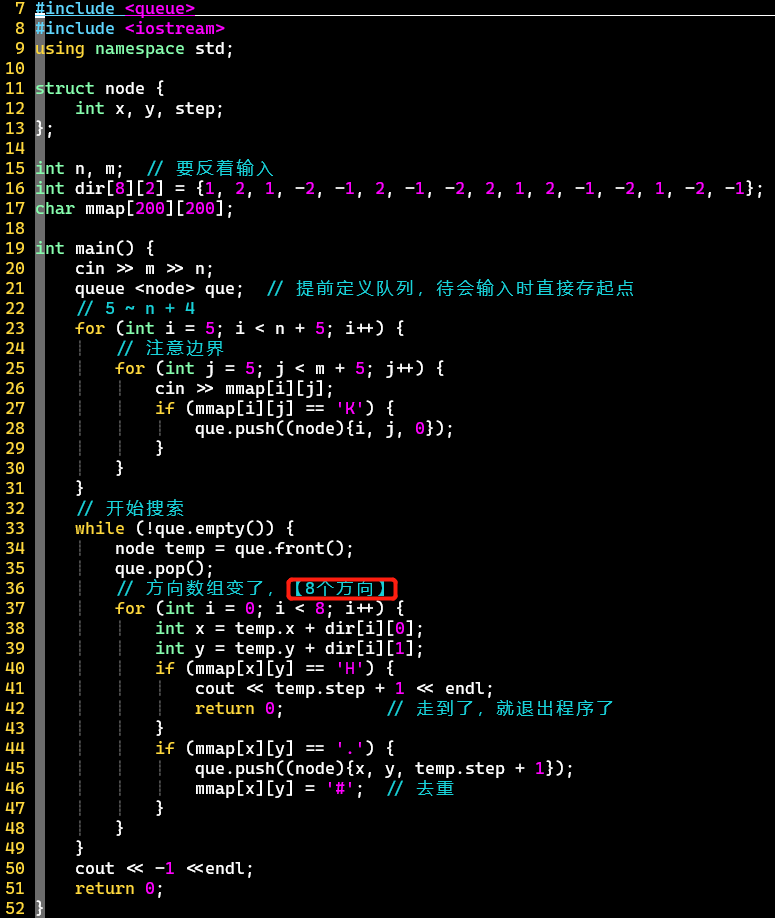
- 基本模板题,关键在方向数组变了
-
HZOJ-398:马的遍历

样例输入
3 3 1 1
样例输出
0 3 2
3 -1 1
2 1 4
- 思路
- 从起点往外搜,仍为8个方向
- 【疑问】
- 是否是地图?什么障碍都没有,就是一个数组
- 如何去重呢?同样利用数组,判断位置上的值
- 判断边界呢?基于数组,判断方便
- 若不判断,需把所有点右移下移一位考虑,且要把外面2圈做成障碍,麻烦!
- 一个大数组num[405][405]:既存答案,又去重
- 【题意】不可达输出-1,起点输出0
- 两种初始化方式
- [孬]初始化为0:需要两个特判,一个到不了的点[0 → -1],起点[0]
- 🆗初始化为-1:完美
- 代码
-
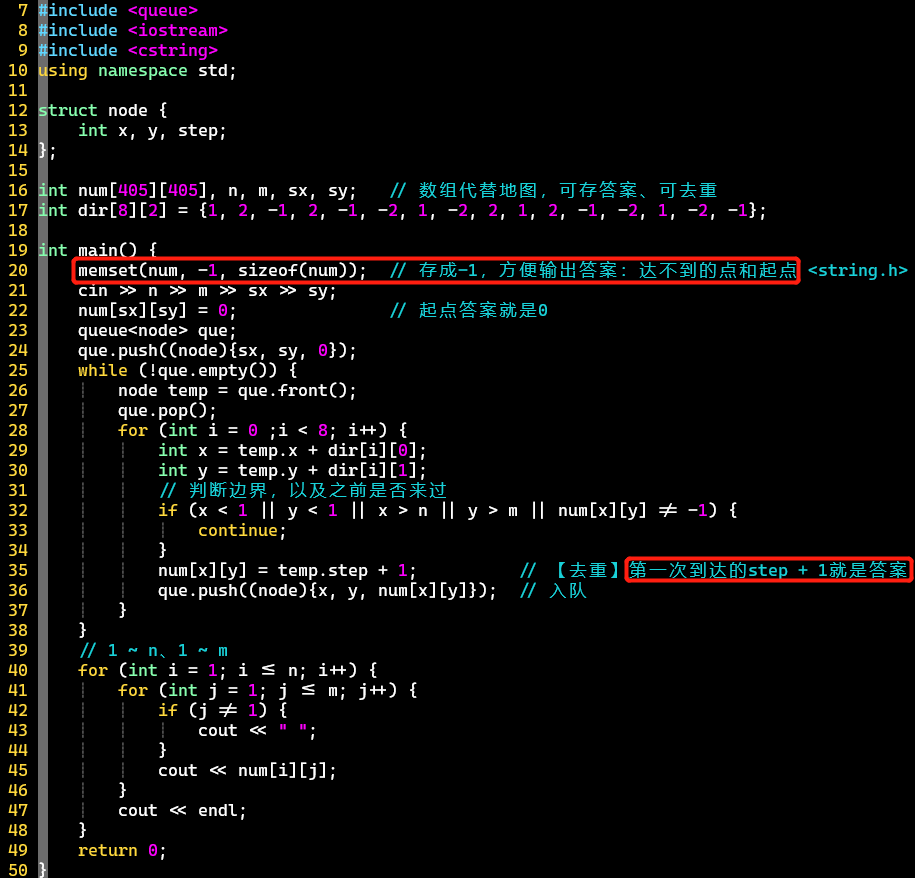
- 题意里的坐标是[1, 1]算起的,但还要判断边界,因为马走法要预留2圈,且没有将边界设置障碍
- 用数组num代替地图,还存答案、去重
- memset -1是精髓
-
HZOJ-400:奇怪的象棋游戏

样例输入
12 16
18 10
样例输出
8
9
- 思路
- 棋盘大小固定为500 * 500
- 12个方向,2次搜索,一个套路
- 代码
- 注意第2次搜索的可能优化,碰见走过的点,直接用当前步数加上 [上一次搜索答案 - 存的步数]
- 直接看下一题,方法更有意思
HZOJ-401:奇怪的象棋游戏升级版

样例输入
2
12 16
18 10
样例输出
8
9
- 思路
- 搜索高达2000次,上题的思路肯定超时
- ⭐终点固定,从[1, 1]往外走,记录一个答案数组
- 这里从起点到终点和从终点到起点的答案一样,注意根据题意来
- 思路反过来后,类似OJ-398题了
- 代码
-
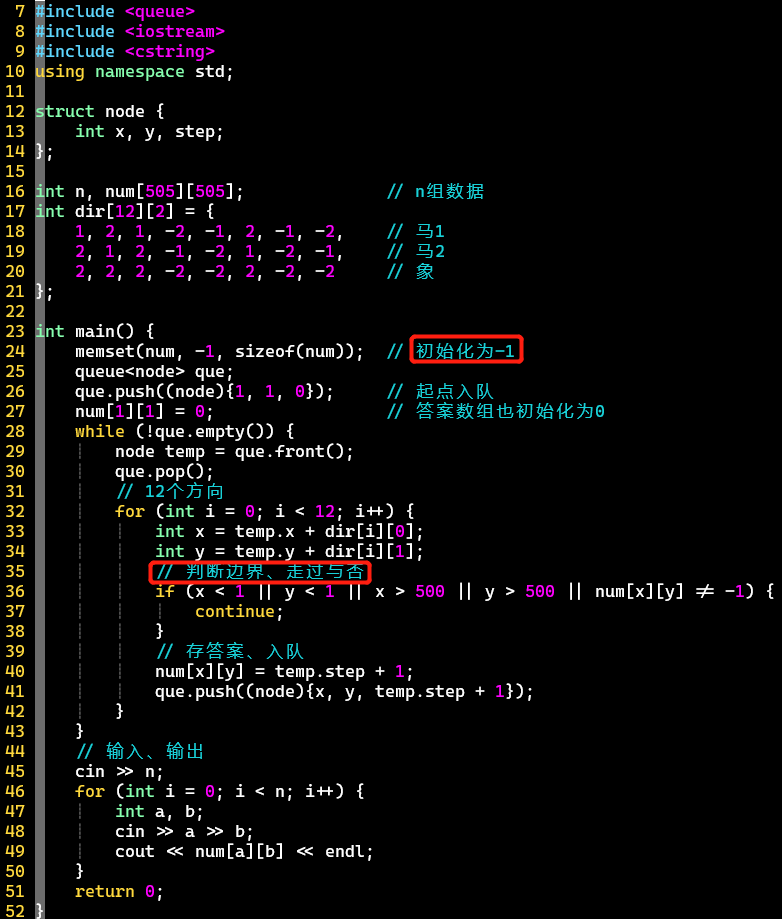
- 同样memset -1,考虑起点步数为0
- 本题棋盘足够大,不需要考虑走不到的情况,走不到一般是棋盘奇小
-
HZOJ-303:矩阵距离一


样例输入
3 4
0001
0011
0110
样例输出
3 2 1 0
2 1 0 0
1 0 0 1
- 思路
- 输入:char!待会判断边界可用
- 这个距离其实就是一个一个走的步数
- 同上题思路,终点变起点,但有多个起点,且本题有输入地图
-

- 从每个起点开始,依次4个方向走1步,走完就下一位
-
- 代码
-
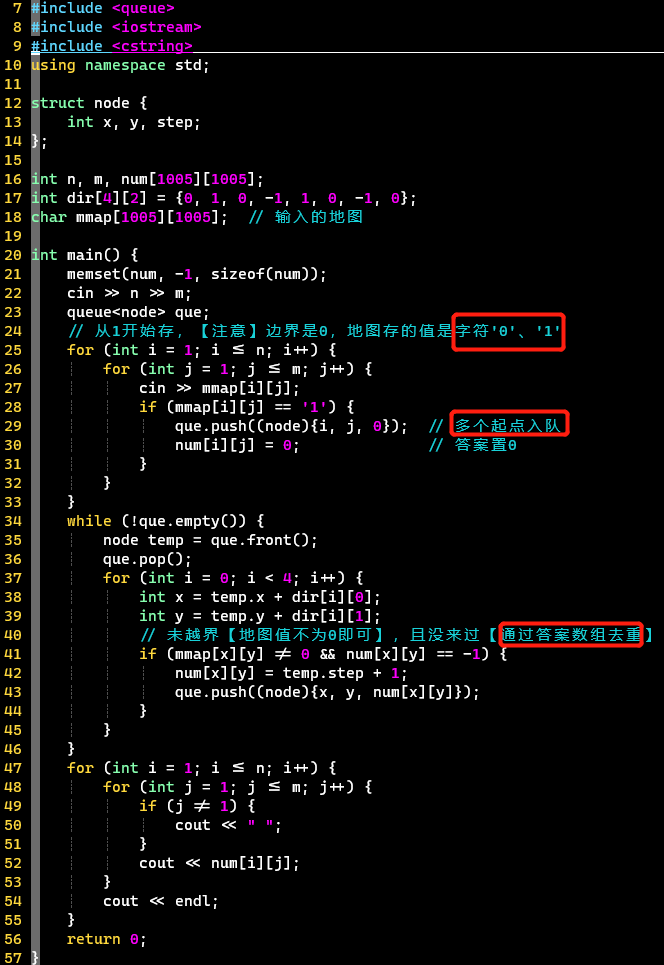
- 同样,memset初始化num为-1
- 通过答案数组去重,地图保持不变
- 答案数组可以和地图统一为一个吗?不行,输出需要用到答案数组,方便输出-1,也方便理解
-
HZOJ-305:乳草的入侵
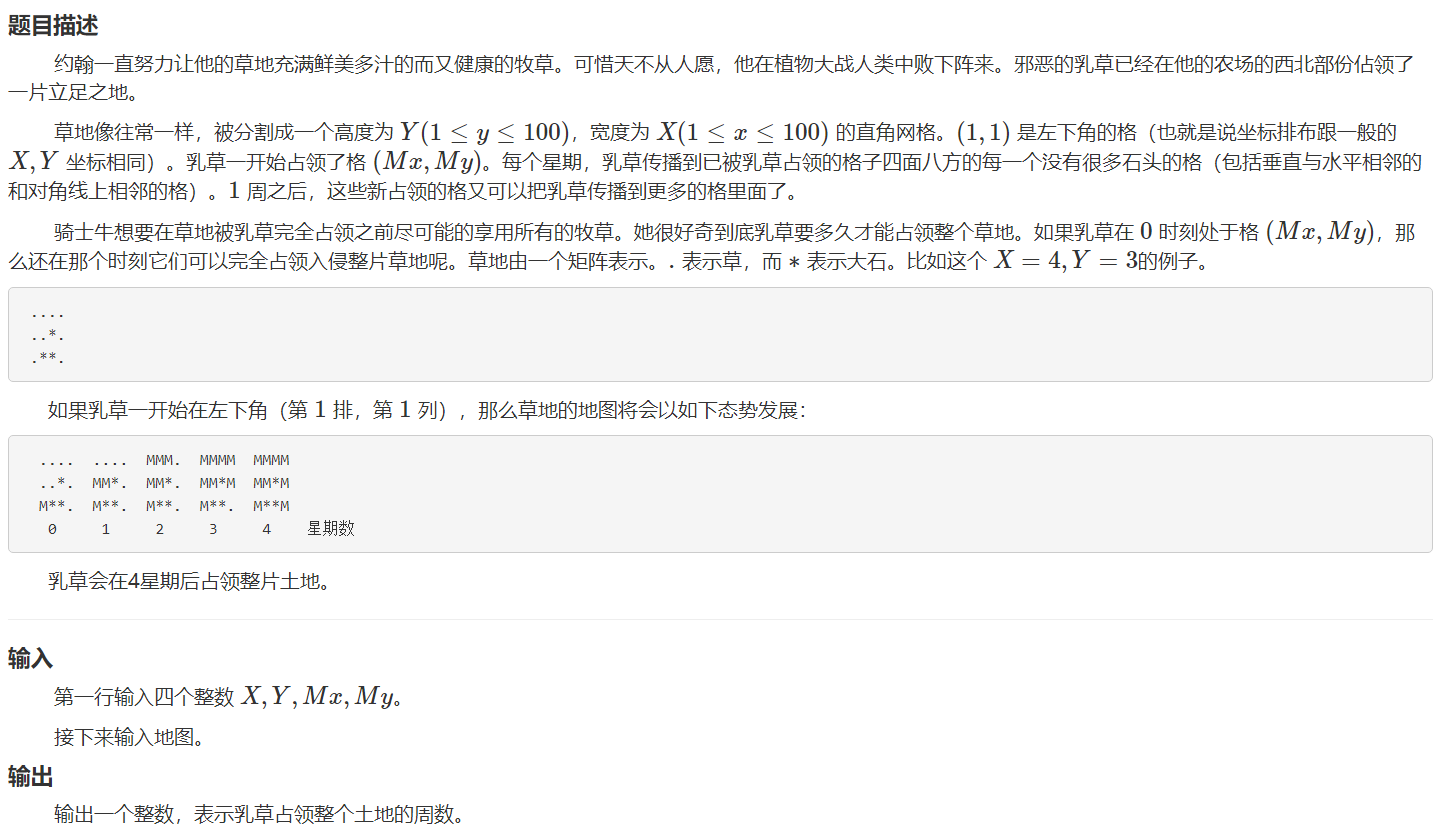
样例输入
4 3 1 1
....
..*.
.**.
样例输出
4
- 思路
- 输入:行列数调换、起点坐标(1, 1)是左下角的格
- 起点坐标同样也是反的
- 把(1, 1)点当作(Y, 1)点
- 原则:以我们常用的坐标系为准,调整到我们的坐标系中
- 8个方向
- ⭐新的套路:没有终点,遍历完就是结果
- 终止状态:队列为空
- 如何记录最远步数?用一个变量!
- 输入:行列数调换、起点坐标(1, 1)是左下角的格
- 代码
-
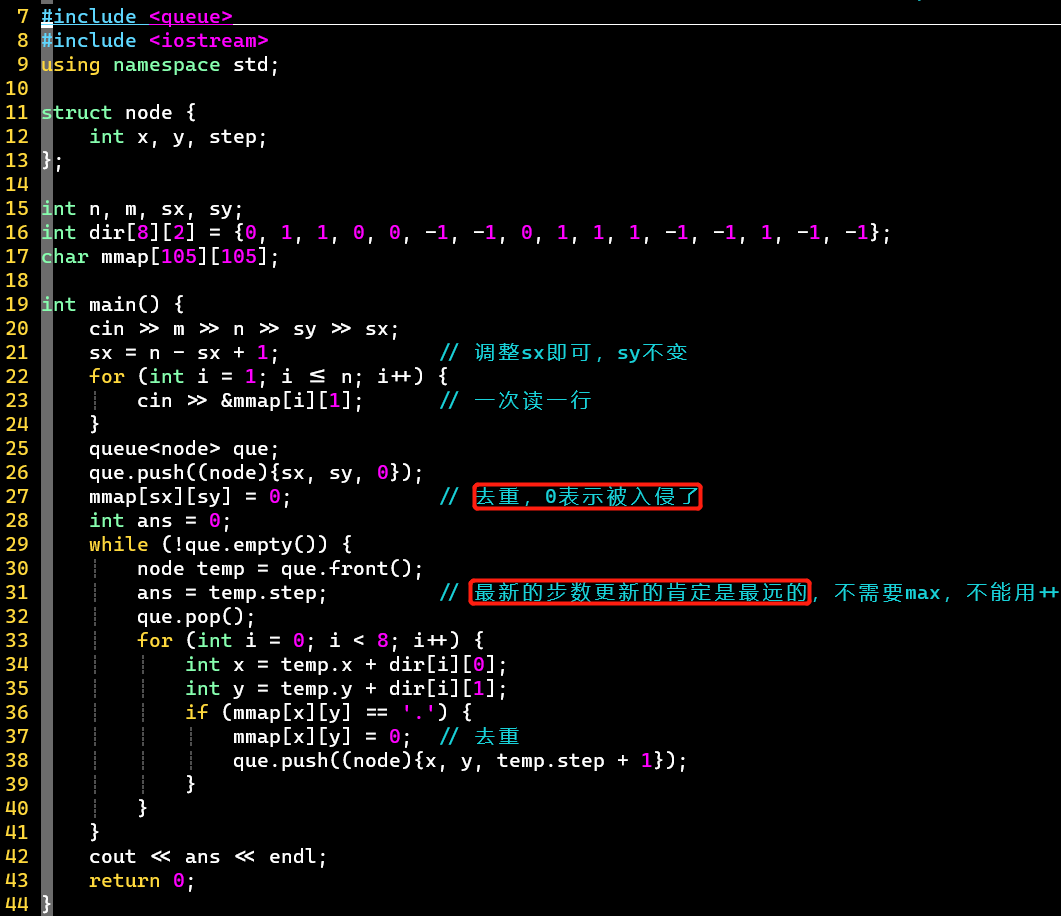
- 注意输入、去重、最远的步数记录
-
HZOJ-529:龙与虫

样例输入
3 4
OXXO
XXOO
XOOO
3 2 2 4
3 3 1 1
0 0 0 0
样例输出
1
Impossible!
- 思路
- [孬]直接从起点广搜;每走一步就判断:通过方向数组循环+1,再一一做判断,判断非常多
- ⭐反转思维,但又不完全反转
- 先从敌人出发,通过方向数组标记所有能被直接干掉的点,作为【终点集合】
- 再从起点广搜,只有当虫子【移动到】终点集合里才能干掉敌人,输出此时的步数
- 多组数据,使用标记数组
- 原地图不能变,还需要用
- 开额外的数组做标记:用1标记终点、用2标记走过的点
- 对每组数据,重新创建该数组或清空皆可
- 标记敌人是关键
- 代码
-
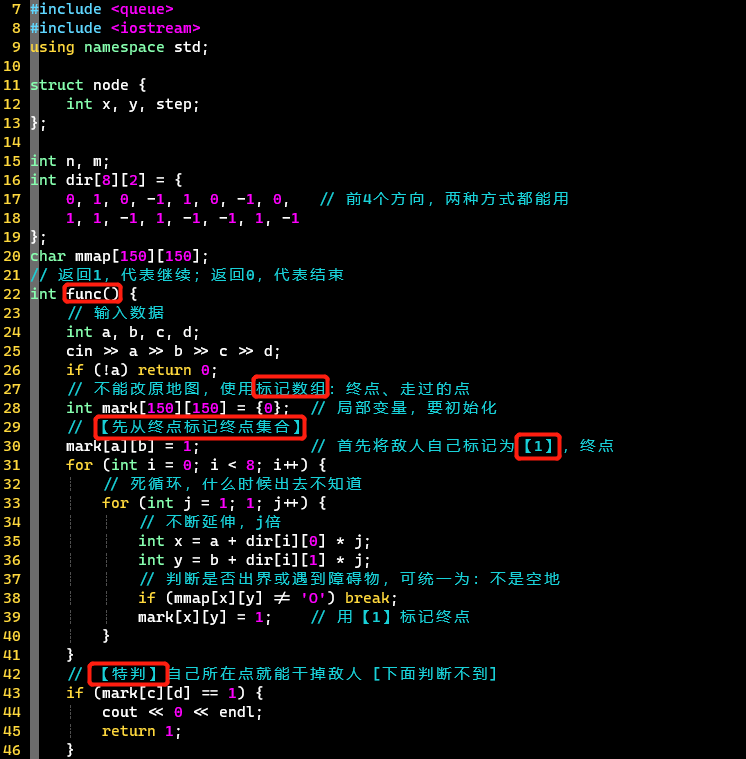
-
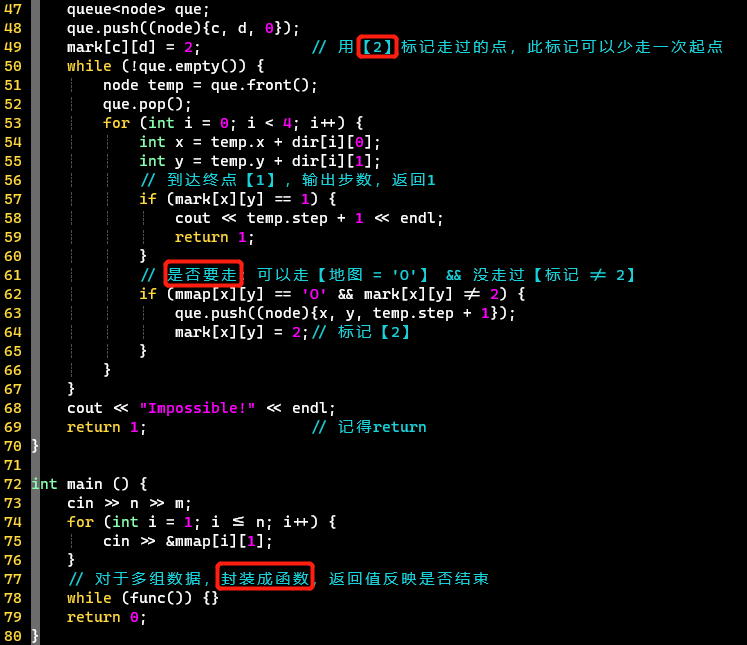
- 题意:坐标从[1, 1]开始
- 对于【多组输入】数据,封装成函数,否则需要用flag标志是否结束,因为会有两层循环
- 标记数组是局部变量,对于每次输入数据都是全新的
- 广搜或方向数组遍历的时候别忘记【自己】的情况,因为其判断不到
- 不标记起点也没错,但是多走一次起点
-
HZOJ-527:飞跃原野

样例输入
4 4 2
PLLP
PPLP
PPPP
PLLP
样例输出
5
- 思路
- 起点:[1, 1];终点:[m, n]
- 飞行距离有限,为D,等同于总能量
- 【1】去重需要增加一个维度:剩余能量
- 因为:数据范围小 100;且不同剩余能量对于不同的可能走法,需区分
- 创建三维数组:点的坐标x y、剩余能量
- 元素值[标记]:就用0、1即可
- 自定义结构也多一维,记录此时的剩余能量
- 【2】走 or 飞
- 飞的范围:2 ~ 剩余能量,只有 ≥ 2步的飞才有意义,不然走还省能量
- 代码
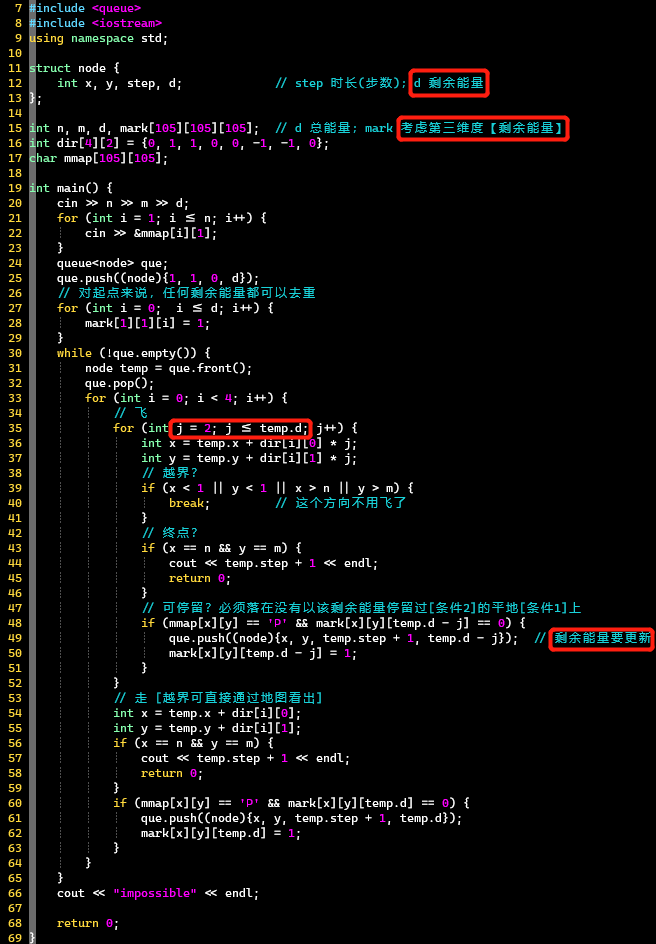
- 【关注】增加剩余能量维度去重、飞的方式
- 注意:飞里面是break
- [PS] 在能量足够的时候,这种暴力枚举的方式其实会有一些无效的【回飞】的情况,但是也只会在最优的步数里走出无效的情况。这其实是由三维去重数组导致的
虽然对某个剩余能量的坐标去重了,但对于PPPPP(12345)这样的情况,如果能量足够,会有1-3-5-3-5-3这样的走法
附加知识点
- C++里自带全排列函数next_permutation、prev_permutation
- 参考STL中的全排列函数
- 但其实不是很好用,自己实现更灵活
思考点
⭐搜索套路:5步走
- 存、起、终、转、重【详见下一章:7 搜索综合问题】
Tips
- 寻路算法:可以参考A*搜索算法——Wiki,等