Bo2SS

完美是不断改进

文章目录 站点概览

Bo

凡事都一笑而过，还有什么意思呢

75 文章
26 分类
26 标签

1 从递推到动态规划（上）

发布于 2020-12-27 | 分类于 计算机 、 海贼班 、 编程算法 | 17分钟 | 3935字数 | 浏览量：

递推算法👉动态规划

课程内容

递推

兔子繁殖问题 [引入]

  • 图片
  • 题意理解：幼年兔子出生后，过一个月变成成年兔子，再过一个月生下一对幼年兔子 [即第三个月]
  • 本月数量 f(n)= 本月成年 + 本月幼年 👇
    • 图片
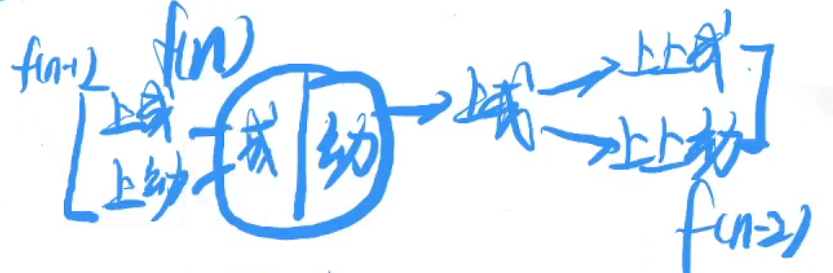
    • 本月成年 = 上个月成年 + 上个月幼年 =上个月数量 f(n - 1)
    • 本月幼年 = 上个月成年 = 上上个月成年 + 上上个月幼年 =上上个月数量 f(n - 2)[新增兔子数量]
    • 👉f(n)=f(n−1)+f(n−2)f(n) = f(n - 1) + f(n - 2)<斐波那契数列>，f(n) 代表第n个月兔子的总数量
  • 当 n = 60 时，单纯用递归实现，会出现
    • 程序运行效率问题 [重复计算递推项]
      • 解决方法：正向递推 + 记忆化 [递归] 或 逆向递推 [循环]
      • 任何一个递推问题，都至少有上述2种方式实现
    • 结果溢出问题 [超过整型表示范围]

求解套路⭐

  • ① 确定递推状态【⭐⭐⭐】：寻找问题中的自变量和因变量
    • 一个数学符号 ➕ 一段对数学符号的描述 [语义信息]
    • 确定状态定义的重点：状态维度。如何确定？
      • 首先确定因变量，再确定相关联的自变量，得维度
      • f(x)=yf(x) = y
      • y：问题中的求解量，也是我们所谓的因变量
      • x：问题中直接影响求解量的部分，也是我们所谓的自变量
    • [PS] 看别人题目解答时，重点关注本步骤；[本质]
  • ② 推导递推公式：分析状态中的容斥关系
    • 推导递推状态符号的自我表示方法
      • 【容斥原理】
      • 图片
      • 整体面积 = 部分面积相加减
    • 👉【相同符号表示下】的公式关系：保持递推状态的定义。如兔子问题中：
      • 图片
      • f(n)一直是所有兔子的数量，不要偏移到成年或幼年兔子的数量，但可以通过它们来转换
        • f(n)=f(n−1)+f(n−2)f(n) = f(n - 1) + f(n - 2)
        • f(n−1)f(n - 1)，代表第n - 1个月的兔子数量 [恰巧等于第n个月的成年兔子数量]
        • f(n−2)f(n - 2)，代表第n - 2个月的兔子数量 [恰巧等于第n个月的幼年兔子数量]
        • 所谓的推导，就是推导上面这两句话
  • ③ 程序实现[递归+记忆化 or 循环]

动态规划

数字三角形问题 [引入]

【动态规划的基本题】HZOJ-43

  • 图片
  • 记录每一行每个点可以走出的最大值
  • ① 从下往上走
    • [首先直接由原值确定最下一行的最大值，通过最大值决策，从下往上依行得到每个点对应的最大值]
    • 递推状态：f(i,j)f(i, j)代表从底边走到点(i,j)(i, j)的最大值
    • 递推公式：f(i, j)=max(f(i+1, j), f(i+1, j+1))+val(i, j)f(i,\ j) = max(f(i+1,\ j),\ f(i+1,\ j+1)) + val(i,\ j)
      • 通过max【决策】，选择从左下角f(i+1,j)f(i + 1, j)或右下角f(i+1,j+1)f(i + 1, j + 1)中的一个状态【转移】，该过程又叫状态转移过程
  • ② 从上往下走
    • [与上述过程相反]
    • 递推状态：f(i, j)代表从顶点走到点(i, j)的最大值
    • 递推公式：f(i, j)=max(f(i−1, j), f(i−1, j−1))+val(i, j)f(i,\ j) = max(f(i-1,\ j),\ f(i-1,\ j-1)) + val(i,\ j)
      • 决策从左上角还是右上角转移过来
  • ❗❗ 从上面两种方式可以看出，状态定义极其重要！
    • 数字符号完全一致
    • 语义信息不同
    • 递归公式不同
    • 【结论】数学符号无法完全代表状态定义，重点在后面的解释！
  • 🆒 两种方法的对比
    • 本质：状态定义的对比
    • 区别主要在程序实现上
    • 第1种更优秀
      • 不用做边界判断；最终结果，直接存储在f[0][0]上
    • 第2种
      • 需要做边界判断；最终结果，存储在一组数据中
      • Ⅰ) 边界判断，是因为上一个状态可能不存在 👉 可使用补0大法
      • Ⅱ) 获取答案，需要遍历一组数据 / 提前存好

本质理解及求解套路⭐

动态规划是递推问题的一种特殊类型

  • 动态规划：递推问题中求解最优解的问题
  • 类似递推的套路：①确定递推状态⭐⭐⭐、②递推公式，③证明正确性，④程序实现
    • 图片
    • 理解第二步：转移、决策
      • 关注所有决定 f(i, j)最优值的状态 [可转移的]，放入到决策过程中
      • 决策，如max；再转移
    • 勤于第三步：正确性证明 [数学归纳法见下]
    • 相比递推主要多了正确性证明，主要验证状态转移方程的正确性
  • [可扩展的概念]最优子结构、无后效性、重复子问题等
  • [可参考的视频]数据结构[国家精品课]-清华大学：P29~P47——bilibili

+ 数学归纳法

  • 图片
  • 可用于证明动态规划的正确性
  • 可用于推导动态规划的转移方程

+ 拓扑序

  • 图形结构是最最抽象的数据结构，必须理解成思维逻辑结构 [神经网络已经具象化了]
  • 引入：在程序中，图形结构不能用循环来遍历，而一维序列可以
  • 本质：图形结构 👉 一维序列
  • 想象：A为起床，B、C分别为穿上、下衣，D、E分别为刷牙、洗脸，F为出门
    • 则其对应的图形结构和转换的拓扑序如下：
    • 图片
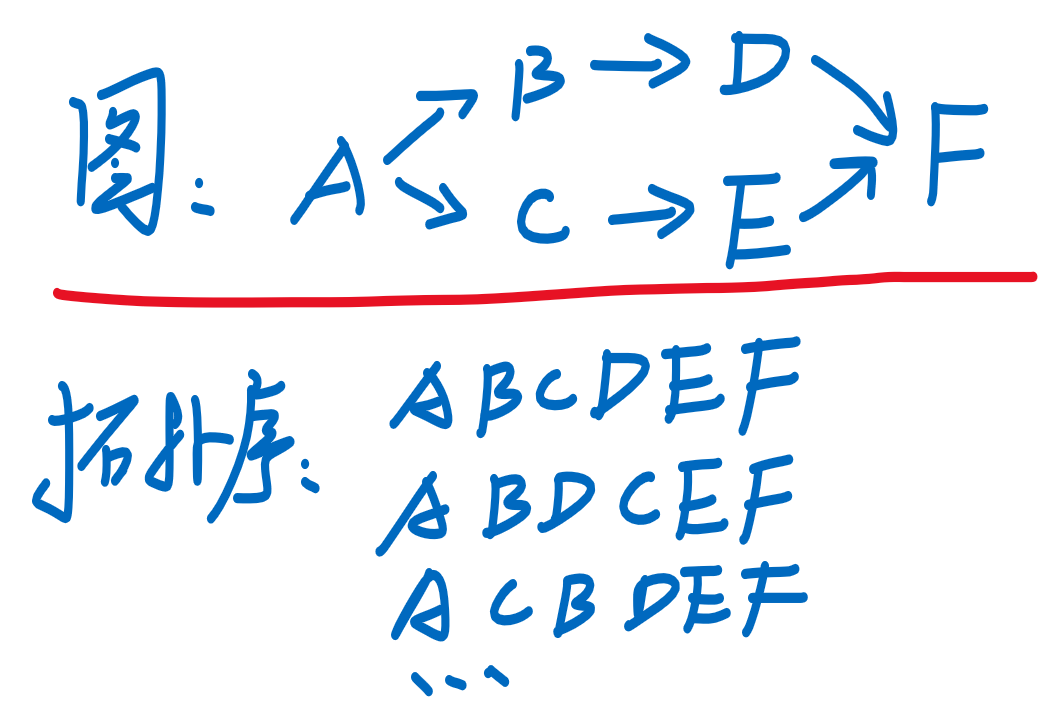
    • 转换过程：不断提取入度为0的元素 [第一个为A]，并将其从图中拿掉
    • 可见一个固定的图结构，其拓扑序不唯一
  • 👇 所有递推问题的状态转移过程[状态之间的求解顺序]，本质上也满足拓扑序
    • 图片
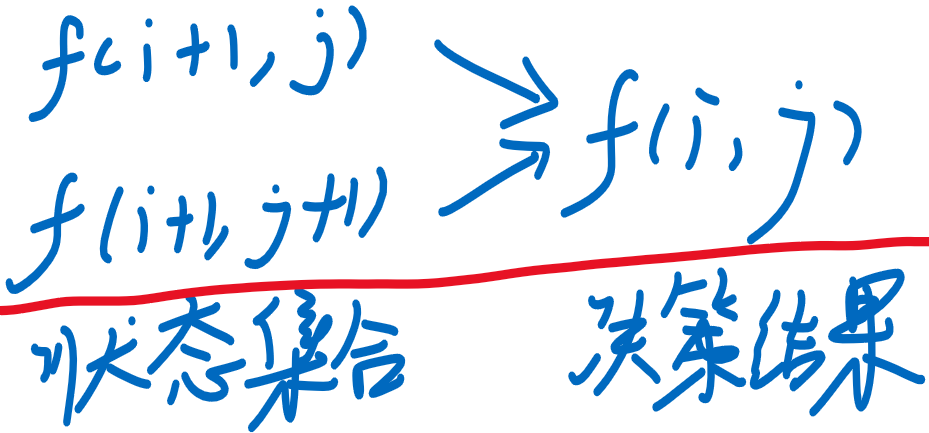
    • 参考数字三角形问题
    • 必须先知道状态集合所有元素的值，才能得到最终的决策结果 [存在依赖关系]
  • [小结]
    • 拓扑序是一种图形结构上的依赖顺序，一个图的拓扑序不唯一
    • 掌握拓扑序的话，可以更好地理解递推问题 [动态规划]
    • 将其理解成一种思维方式！

求解方向

针对递推问题 [动态规划]

  • ① 我从哪里来
    • 计算前置的所有状态，得到当前状态的结果 [找前面的结点]
    • 例如：数字三角形、兔子繁殖、钱币、墙壁涂色
    • [比“我到哪里去”简单]
  • ② 我到哪里去
    • 当前状态的结果已经正确，要更新后置的所有状态 [找后面的结点]
    • 例如：杂务[P1113]、神经网络[P1038]、旅行计划[P1137]
    • P：来自洛谷上的题

随堂练习

——递推——

爬楼梯

[HZOJ-40]

图片
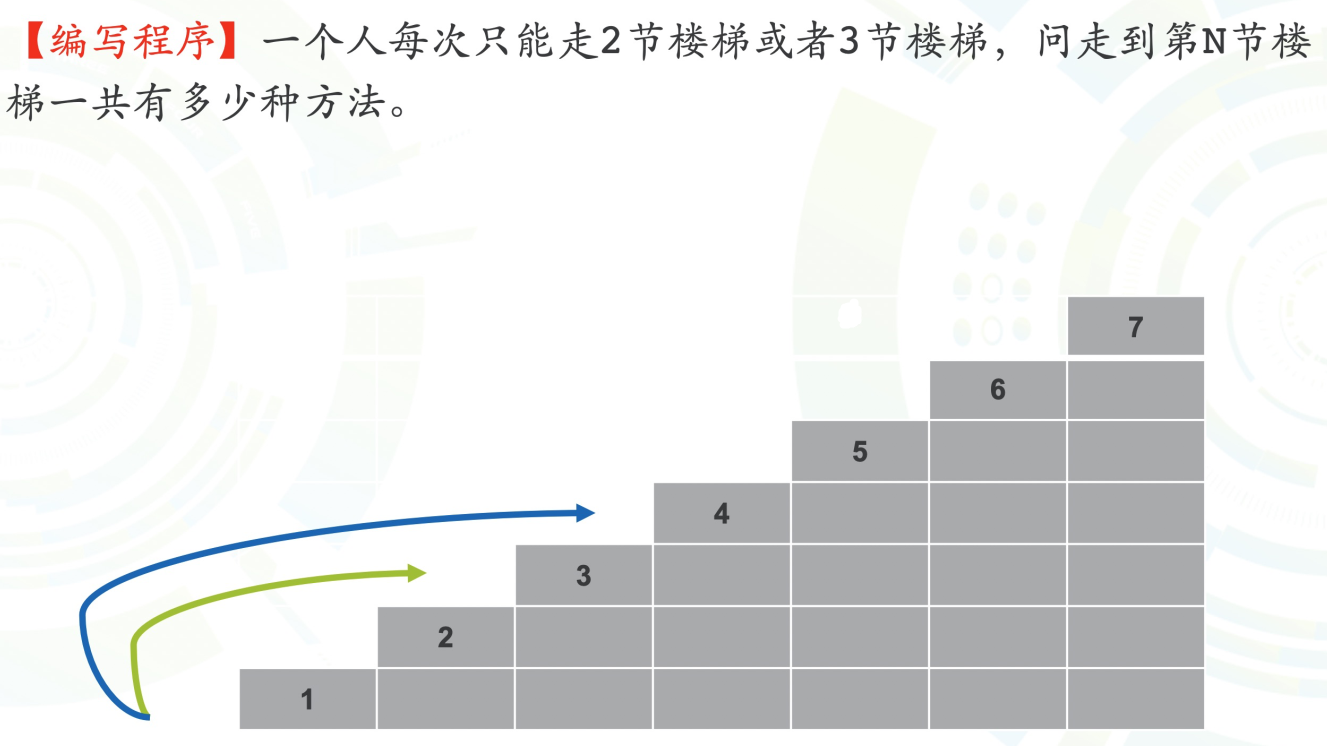
  • 确定递推状态
    • 因变量：方法数
    • 自变量：要上的楼梯数
    • f(n)：上到第n节楼梯的方法数
  • 推导递推公式
    • 根据最后一步是2步还是3步划分f(n)
    • f(n)=f(n−2)+f(n−3)f(n) = f(n - 2) + f(n - 3)

钱币问题

[HZOJ-42]

图片
  • 状态定义
    • 因变量：方法总数
    • 自变量：目标金额、使用的钱币种类
    • f(n)(N) ：使用前n种钱币，凑得目标金额N的方法数
  • 递推公式
    • 基于容斥原理：是/否使用第n种钱币
    • ① 没用第n种钱币：f(n−1)(N)f(n - 1)(N)
    • ② 一定用了第n种钱币：f(n)(N−val(n))f(n)(N - val(n))
      • val(n)：第n种钱币的面额
      • 以上关系为等于关系，即数量正好相等；而非准确的表示关系，式子是自己定义的
  • [PS] 注意：组合问题，不考虑顺序

墙壁涂色

图片
  • 【理解状态定义的重要性！】状态不同，递推公式不同，程序不同
  • 难点：环状，最后一块颜色与第一块颜色有关联
  • 3种方式
    • ①关注首尾颜色【通用，需掌握】
      • 状态定义
        • 因变量：方案总数
        • 自变量：墙壁数量
          • ➕ 解题技巧相关的量：头部颜色、尾部颜色 [需要记录]
        • f(n,i,j)f(n, i, j)：n块墙壁，头部颜色为i，尾部颜色为j的方案总数
      • 递推公式——非环 👉 成环：取出非环的方法中，首尾颜色不一样的方法
        • [先不考虑环]f(n,i,j)=Σf(n−1, i, k) ∣ k≠jf(n, i, j) = Σ f(n - 1,\ i,\ k)\ |\ k \neq j
          • 即n - 1块墙壁，头部颜色为i，尾部颜色不为j[相邻颜色不相同] 的方案总数
        • 【再考虑环，得答案】f(n)=ΣΣf(n, i, j) ∣ i≠jf(n) = ΣΣ f(n,\ i,\ j)\ |\ i \neq j
          • 即在保证了相邻颜色不一样的方案中，首尾颜色不一样的方案总数
    • ②头部颜色是什么不重要 [只改变头部颜色，对应的结果是相等的]
      • 状态定义
        • f(n, j)：n块墙壁，尾部颜色为j的方案总数 [头部颜色默认为0（隐含条件），假设3种颜色的编号为0、1、2]
      • 递推公式
        • [隐含头部颜色为0的条件]f(n, j)=Σf(n−1, k) ∣ k≠jf(n,\ j) = Σf(n - 1,\ k)\ |\ k \neq j
        • 【答案】f(n)=[f(n,1)+f(n,2)]×3f(n) = [f(n, 1) + f(n, 2)] \times 3👉f(n,1)×6f(n, 1) \times 6
          • 6：头部颜色有3种选择，定了头部颜色后，尾部颜色有2种选择，即3 * 2
          • 通过实际的计算保证头尾颜色不一致
    • ③头尾颜色都不关注
      • 状态定义f(n)：n块墙壁，符合条件 [首尾颜色、相邻颜色不同] 的方案总数
      • 递推公式
        • 图片
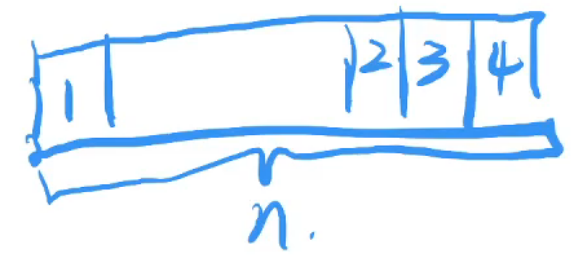
        • 根据上图，f(n)可分为两种情况：1和3相同、1和3不同 [1和4肯定不同，不好划分]
          • (Ⅰ) 1和3不同：f(n−1)×1f(n - 1) \times 1
            • 此时前n - 1块墙壁有合理的涂色，即f(n - 1)种方案
            • 又4号位只剩1种颜色选择，因为1和3不同，1和4不同，3和4也不同
          • (Ⅱ) 1和3相同：f(n−2)×2f(n - 2) \times2
            • 1和3相同，1和2必不同，所以此时前n - 2块墙壁有合理的涂色，即f(n -2)种方案
            • 又4号位还剩2种颜色选择，因为1和3相同，4只要和1不同即可
        • 【答案】f(n)=f(n−2)×2+f(n−1)f(n) = f(n - 2) \times 2 + f(n - 1)，等式仅在n ≥ 4时成立
        • [延伸] 如果颜色种数为k，f(n)=f(n−2)×(k−1)+f(n−1)×(k−2)f(n) = f(n - 2) \times (k -1) + f(n - 1) \times (k - 2)
      • [PS] 太巧妙，需要灵性

HZOJ-41：墙壁涂色

图片
图片

样例输入

5 3

样例输出

30
  • 思路
    • 相比上题，区别在于颜色种数为k，而不是3
    • 使用上述第3种方式：f(n)=f(n−2)×(k−1)+f(n−1)×(k−2) [n≥4]f(n) = f(n - 2) \times (k -1) + f(n - 1) \times (k - 2)\ [n ≥ 4]
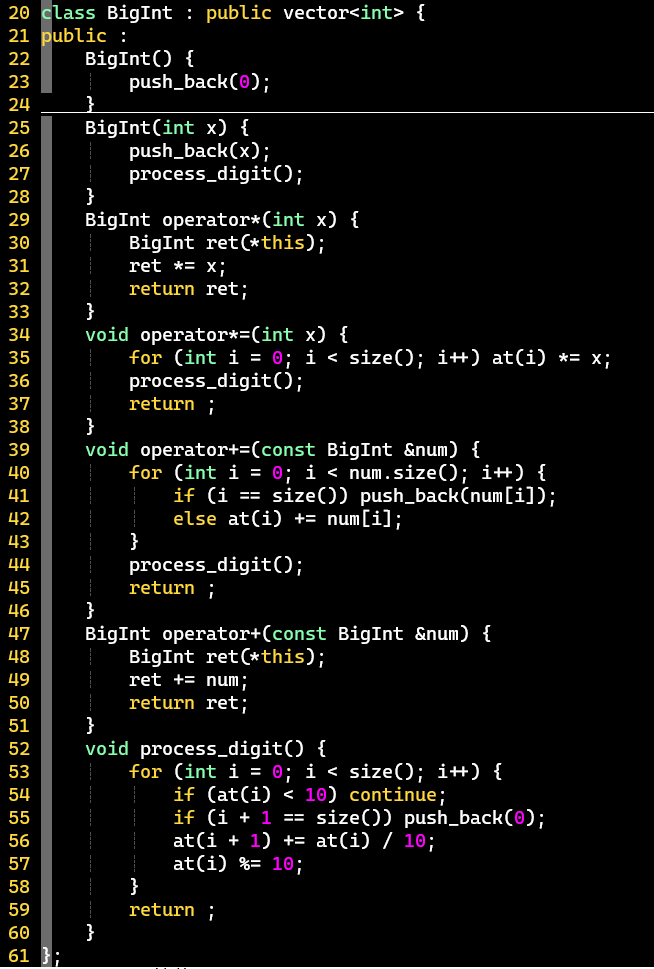
    • 【注意】根据数据规模，方案总数可能变成大整数，需利用数据结构
  • 代码
    • 图片
    • 【算法】利用循环，以及三个数 [需要记录3项状态f] 来回倒，先推算出f(1)、f(2)、f(3)的值
      • f(1)、f(2)、f(3)不满足通用公式 [n ≥ 4]
      • f(3)的值存在f[0]中
      • 模3的使用，让数组滚动起来
    • 【数据结构】对于大整数情况，只需更换数据结构int→BigInt
      • 将f[3]数组的类型从int改为BigInt，再创造BigInt类型、重载cout即可
      • 图片
      • 图片
      • 涉及C++知识 [重载、引用等等]，不是本节的重点
      • 涉及大整数加大整数、大整数乘int型的思想，可参考《面试笔试算法上》——大整数加法、大整数乘法
      • [PS] 程序 = 算法(效率) + 数据结构(表示能力)

——动态规划——

HZOJ-44：最长上升子序列

图片

样例输入

10
3 2 5 7 4 5 7 9 6 8

样例输出

5
  • 思路
    • 普通版
      • 能够挑出来的最长严格上升子序列[不需要连续挑]
      • 状态定义
        • dp(i)dp(i)：代表以索引为ii的元素结尾的最长严格上升序列长度
        • 必须以ii结尾！
      • 状态转移
        • dp(i)=max{dp(j)}+1 ∣ j<i, val(j)<val(i)dp(i) = max\{dp(j)\} + 1\ |\ j<i,\ val(j) < val(i)
        • 所有能够转移到dp(i)dp(i)的状态：满足j<i, val(j)<val(i)j<i,\ val(j)<val(i)条件的f(j)f(j)，共ii个
        • 决策：maxmax
      • 最终答案：max(f(i))max(f(i))，在所有的dp(i)dp(i)中取最大值
      • 状态转移的时间复杂度：O(n2)O(n^2)
    • 优化版——转移过程
  • 代码
    • 普通版
      • 图片
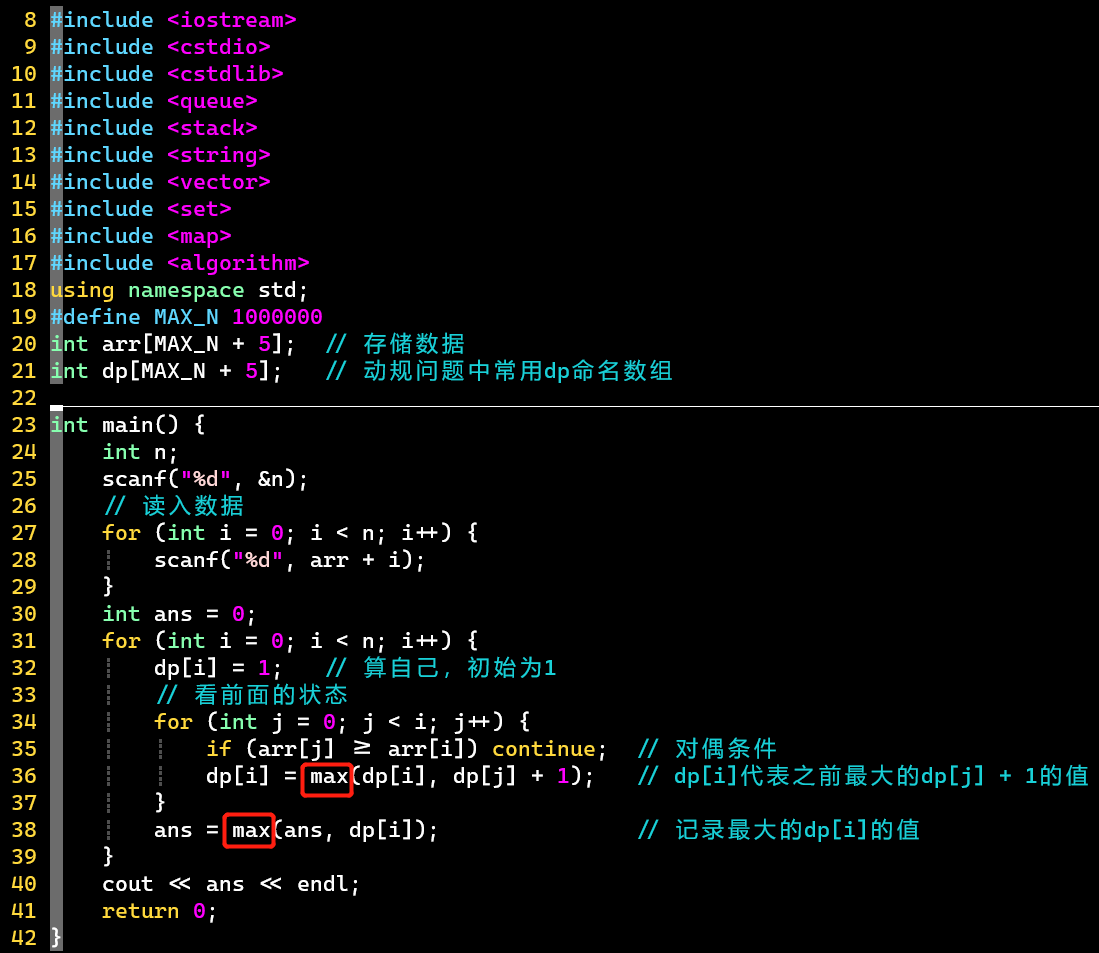
      • 数据很大，使用scanf，而不是cin
      • 注意两个max的含义
      • 状态转移的时间效率低

HZOJ-45：最长公共子序列

图片

样例输入

sehuaizexi
yhaizeyiux

样例输出

6
  • 思路
    • 状态定义
      • dp(i, j)dp(i,\ j)：代表第1个字符串取前 i 位，第2个字符串取前 j 位，对应的最长公共子序列的长度
    • 状态转移
      • dp(i)={max{dp(i−1, j), dp(i, j−1)}s1(i)≠s2(j)dp(i−1, j−1)+1s1(i)=s2(j)dp(i) = \left\{\begin{aligned}&max\{dp(i-1,\ j),\ dp(i,\ j-1)\} &s1(i)\neq s2(j)\\&dp(i-1,\ j-1)+1&s1(i)=s2(j)\end{aligned}\right.
      • ⭐参与决策的状态数量，是会根据条件不同而改变的
        • 取决于【字符串1的第 i 位】和【字符串2的第 j 位】是否相等
        • 待决策的状态数量为2个或1个，上一题的数量为 i 个
        • [PS]
          • 情况2不需要决策，其值一定不小于情况1，因为情况1中dp(i−1, j)dp(i-1,\ j)或f(i, j−1)f(i,\ j-1)最多比情况2中f(i−1, j−1)f(i-1,\ j-1)大1
          • 但情况2加入情况1的决策肯定没错，即在情况2下，dp(i)=max{dp(i−1, j), dp(i, j−1), dp(i−1, j−1)+1}dp(i)=max\{dp(i-1,\ j),\ dp(i,\ j-1),\ dp(i-1,\ j-1)+1\}
      • 状态转移的时间复杂度：O(n×m)O(n \times m)
  • 代码
    • 图片
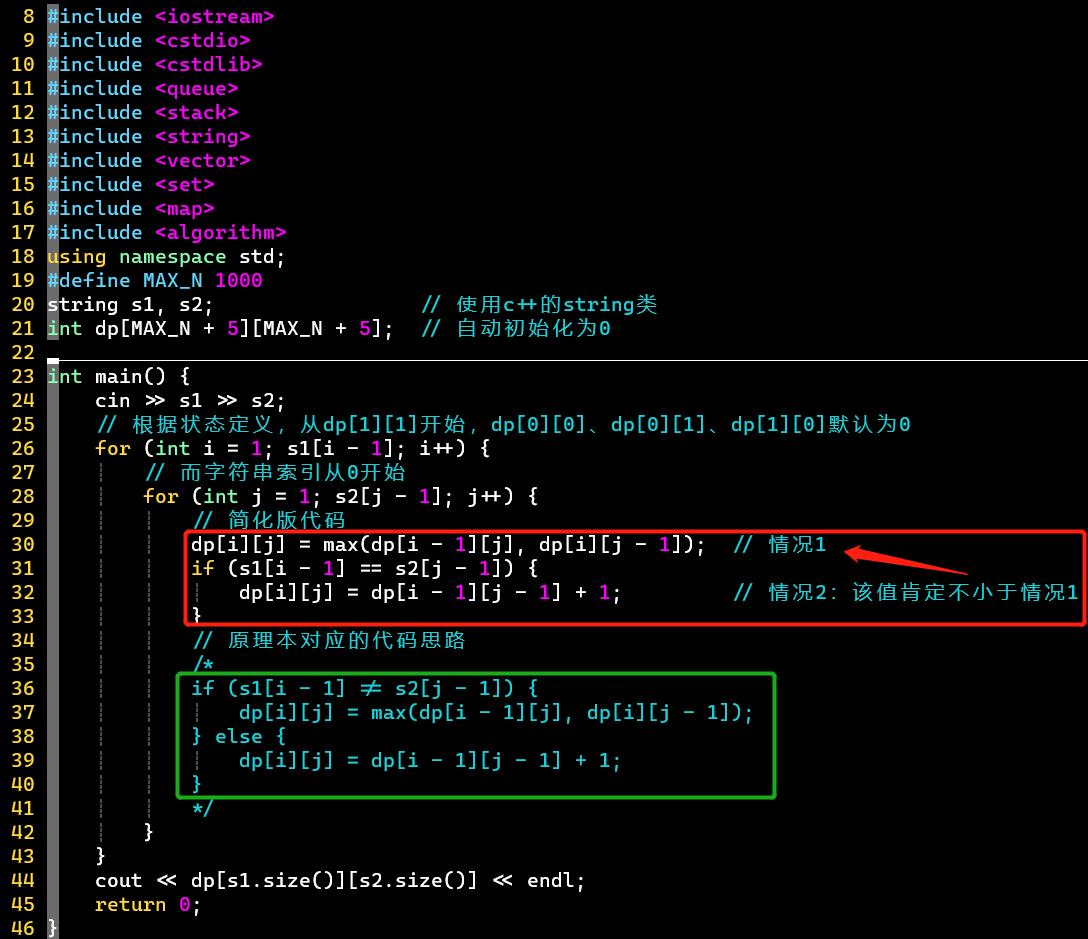
    • 简化版：可以少一行代码，情况2的值肯定不小于情况1
    • 注意：dp从dp[1][1]开始，但字符串索引从0开始

Tips

  • 要把一道题做成一类题
  • vim下快速复制整行——shift + v——visual line模式
  • 有些现象我们可以不理解，但不要轻易去否定，因为最聪明的人不是我们，存在即合理

# 计算机 # 海贼班 # 编程算法