课程内容
三类优化方法
① 状态转移过程的优化
- 不改变状态定义,使用一些特殊的数据结构或者算法专门优化转移过程
- 举例:扔鸡蛋 V2
② 程序实现的优化
- 状态定义没变、转移过程也没有变
- 例如:0/1背包问题,钱币问题 [滚动数组]
③ 状态定义的优化
- 大量训练才能培养出来的能力,从源头进行优化
- 举例:扔鸡蛋 V3
【⭐】 状态定义 -> 源头,转移过程 -> 过程,程序实现 -> 结果
随堂练习
———动态规划——
HZOJ-46:切割回文

样例输入
sehuhzzexe
样例输出
4
- 思路
- 字符串长度50万,注意超时
- 普通版
- 状态定义 [类似最长上升子序列]
- :取字符串的前位,最少分成多少段回文字符串
- 段数更好理解,等价于最少切的刀数 + 1
- 状态转移
-
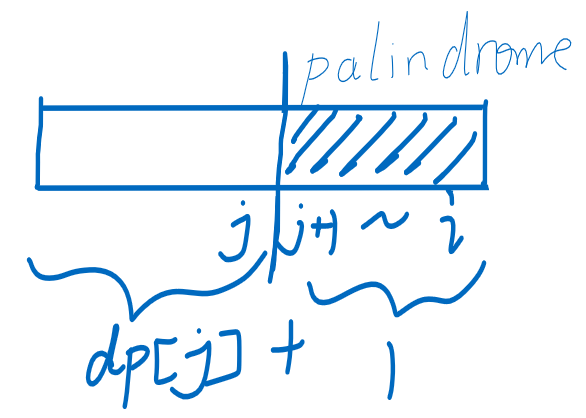
-
- 状态集合:,位置的字符串是回文字符串
- 决策:
-
- 时间复杂度:,可以对转移阶段进行优化
- 状态定义 [类似最长上升子序列]
- 优化版——转移过程
- 现象:实际上回文字符串会非常少
- 优化:提前存储每个回文串的位置
- 即提前处理得到二维数组
- 存储的是所有以位置结尾的回文串们的起始坐标[可能不止一个]
- 因此,在转移过程中,利用处理好的数组,可以避免掉大量的重复循环遍历判断回文串的过程
- 即提前处理得到二维数组
- 状态转移方程 👉
- 状态集合大小:,即该子串中的回文串数量
- 时间复杂度:,代表字符串中回文串的数量
- 代码
- 普通版
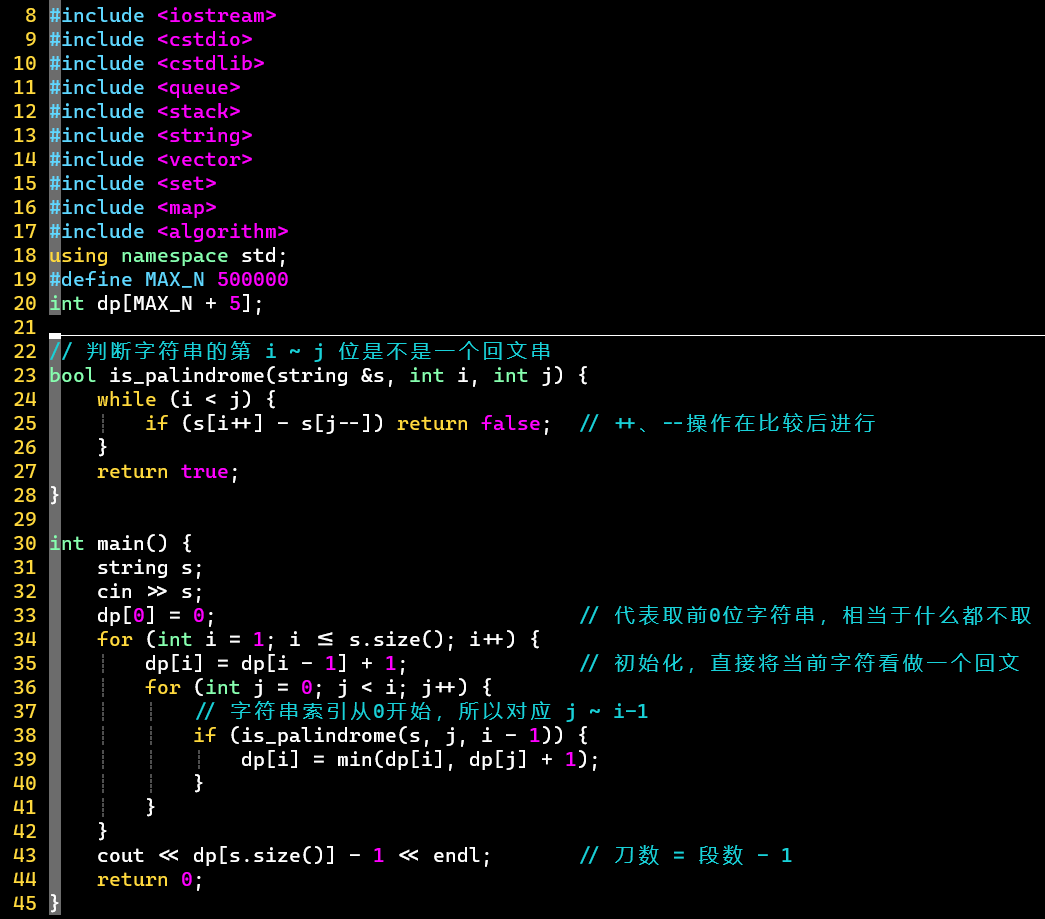
- 字符串和dp数组错开了一位
- for循环的、对应dp数组的索引,判断回文串的、要对应到字符串上,所以各-1
- 初始化,当前字符一定是一个回文 [不管段数,只管可以转移]
- 其实就是的情况
- 时间复杂度:
- 不能单纯看两个循环加判断回文,似乎是,要从均摊时间复杂度的角度考虑
- 优化版
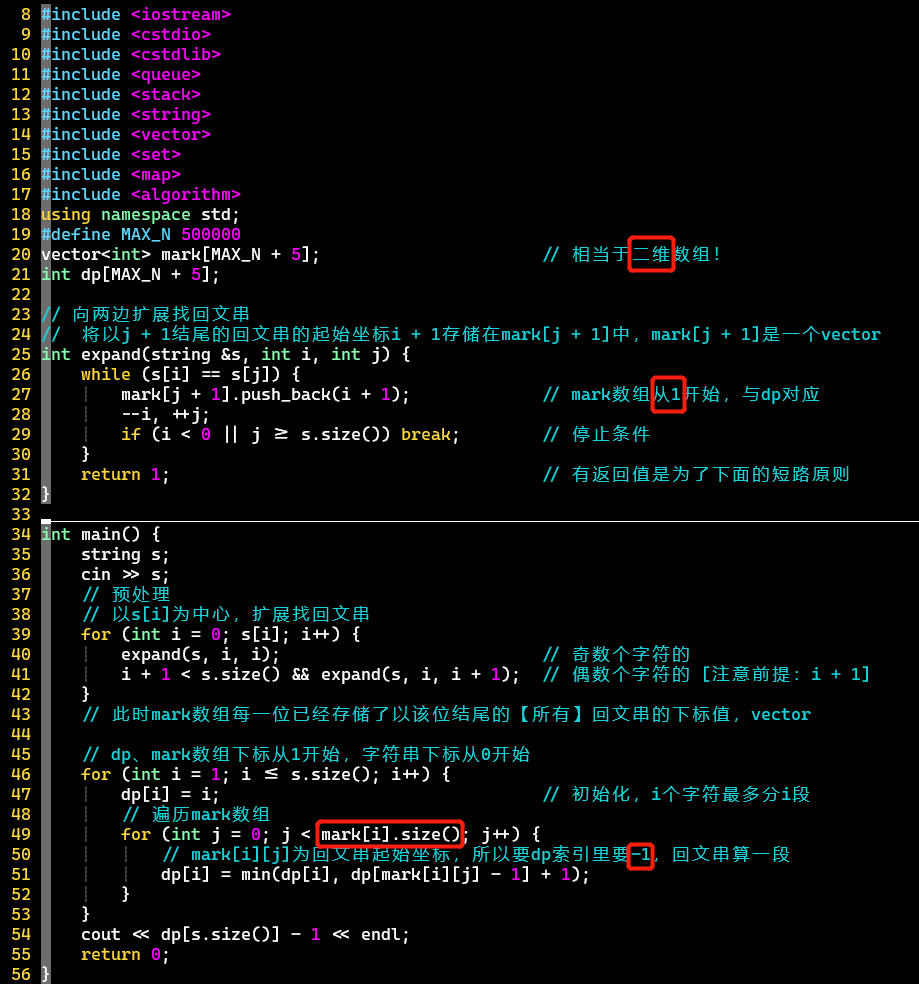
- 【注意】
- 数组是二维的,第一维用vector结构可以不用确定第二维长度 [根据子串的回文串数量变化],也方便添加起始坐标
- 各数组的索引起始点,只有字符串从0开始
- 回文串的扩展思路,由中心向两边,需要考虑奇数和偶数个字符
- 普通版
背包类问题:一类【在有限资源下获得最多回报/最少成本获得最多回报】的问题
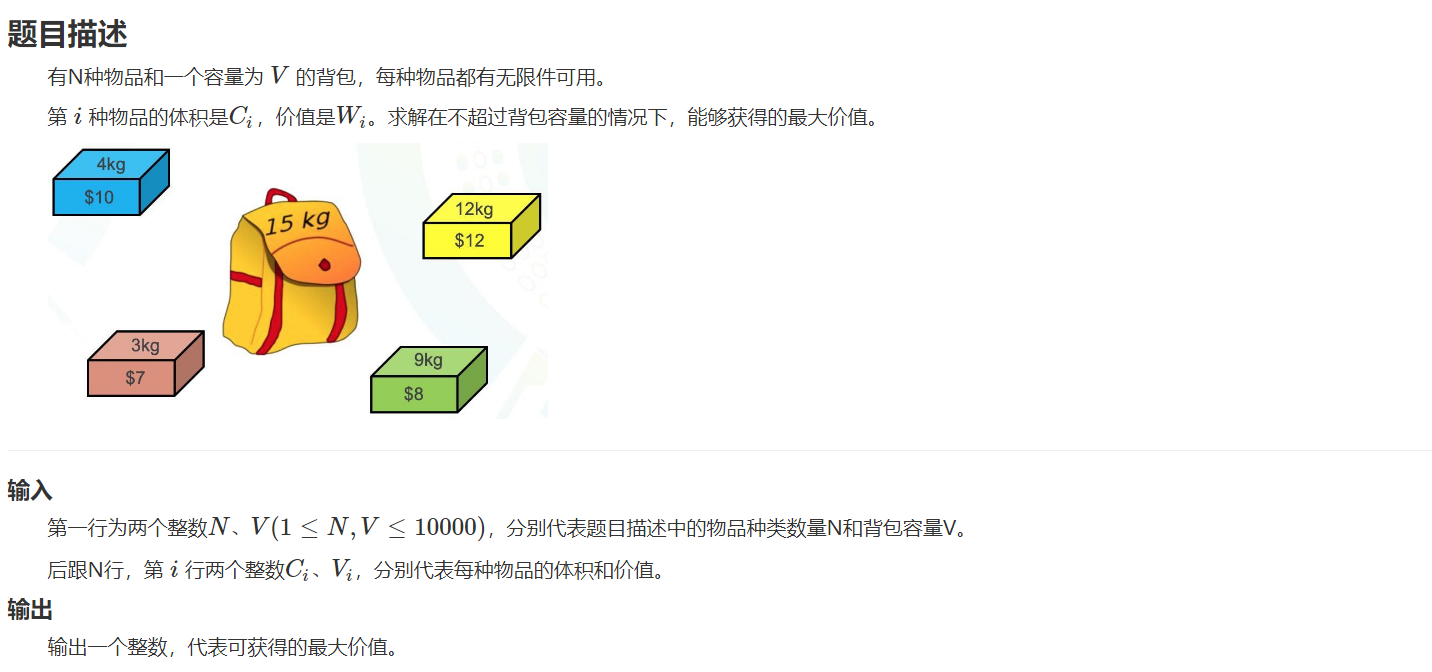
HZOJ-47:0/1背包
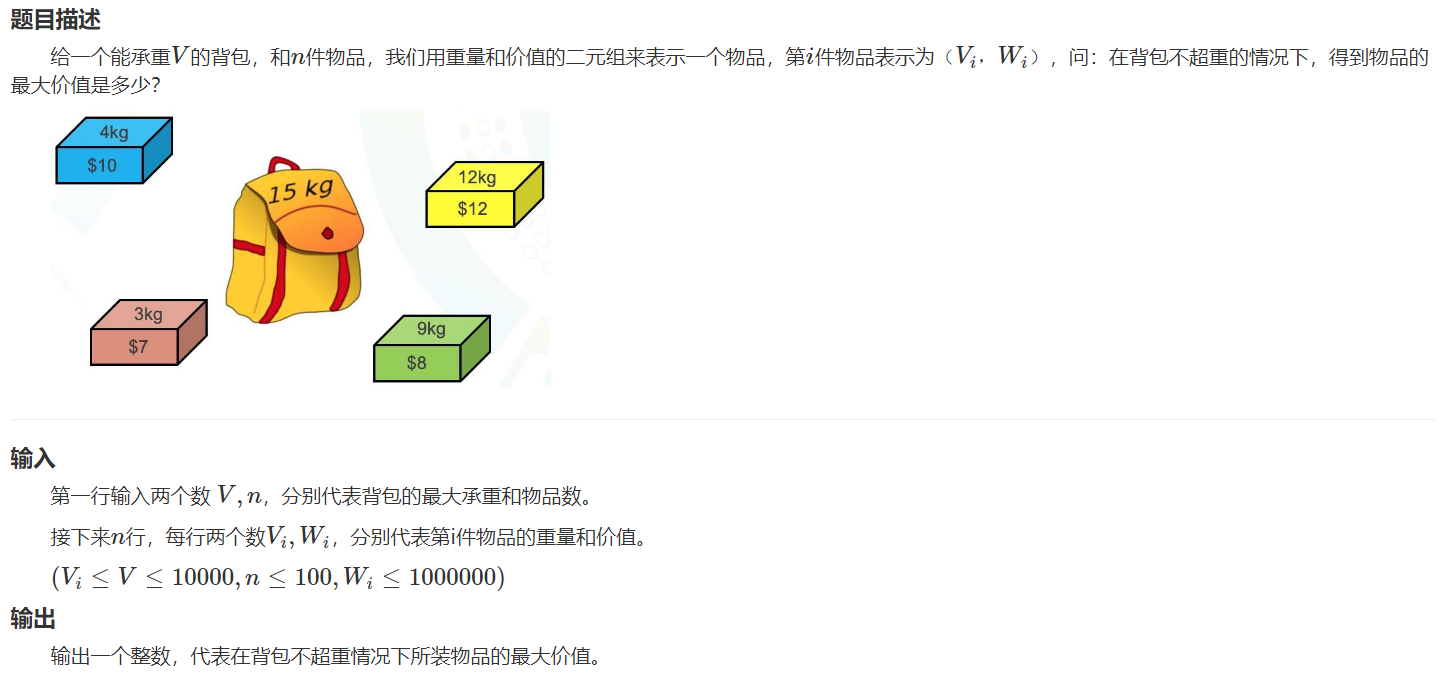
样例输入
15 4
4 10
3 7
12 12
9 8
样例输出
19
- 思路
- 物品数量有限,只有 选/不选 两种状态
- 状态定义
- :前 i 件物品,背包最大承重为 j 的情况下,能够获取的最大价值
- 状态转移
- 状态集合:没选第 i 件,选了第 i 件,共2种状态
- 决策:
- 注意题目中:v代表重量、w代表价值
- 时间复杂度:
- 代码
- V1:状态如何定义,程序就如何实现
-
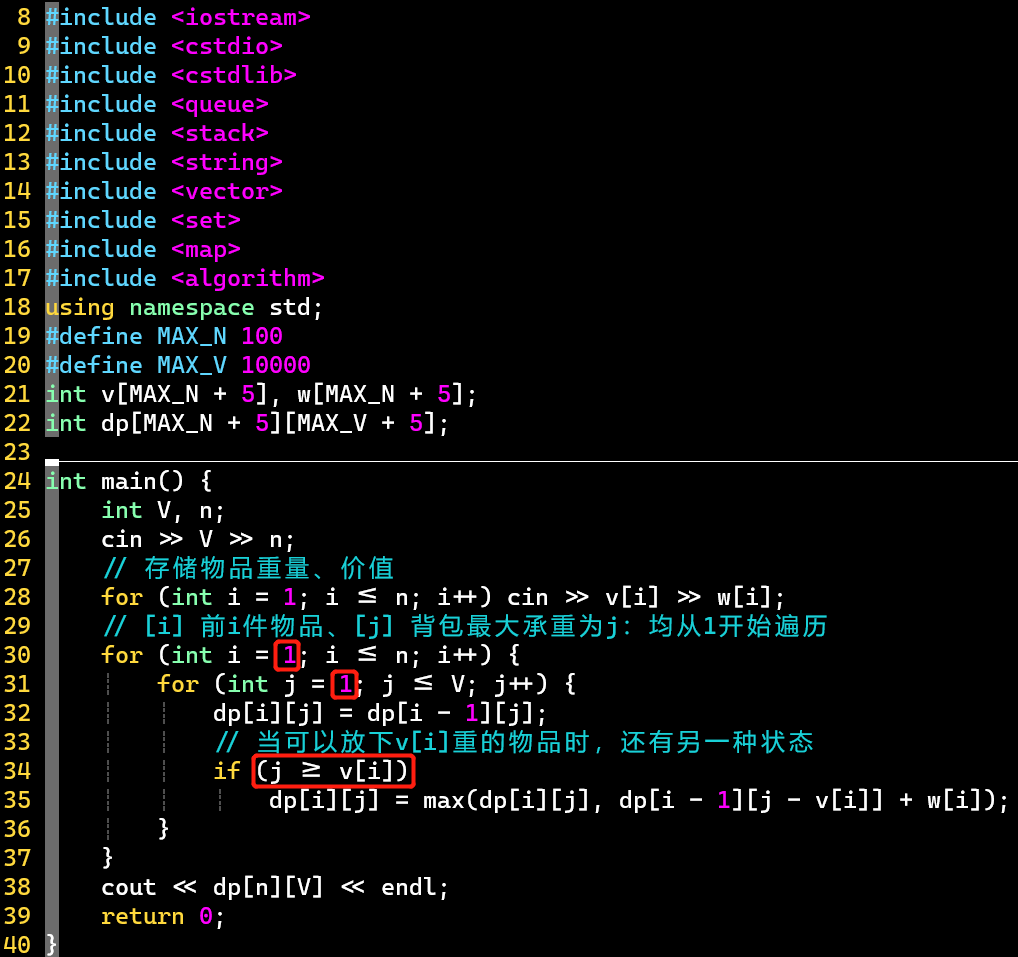
- 注意遍历起点,不要漏状态
- 该种方式不优美
-
- V2:滚动数组 👉 空间优化
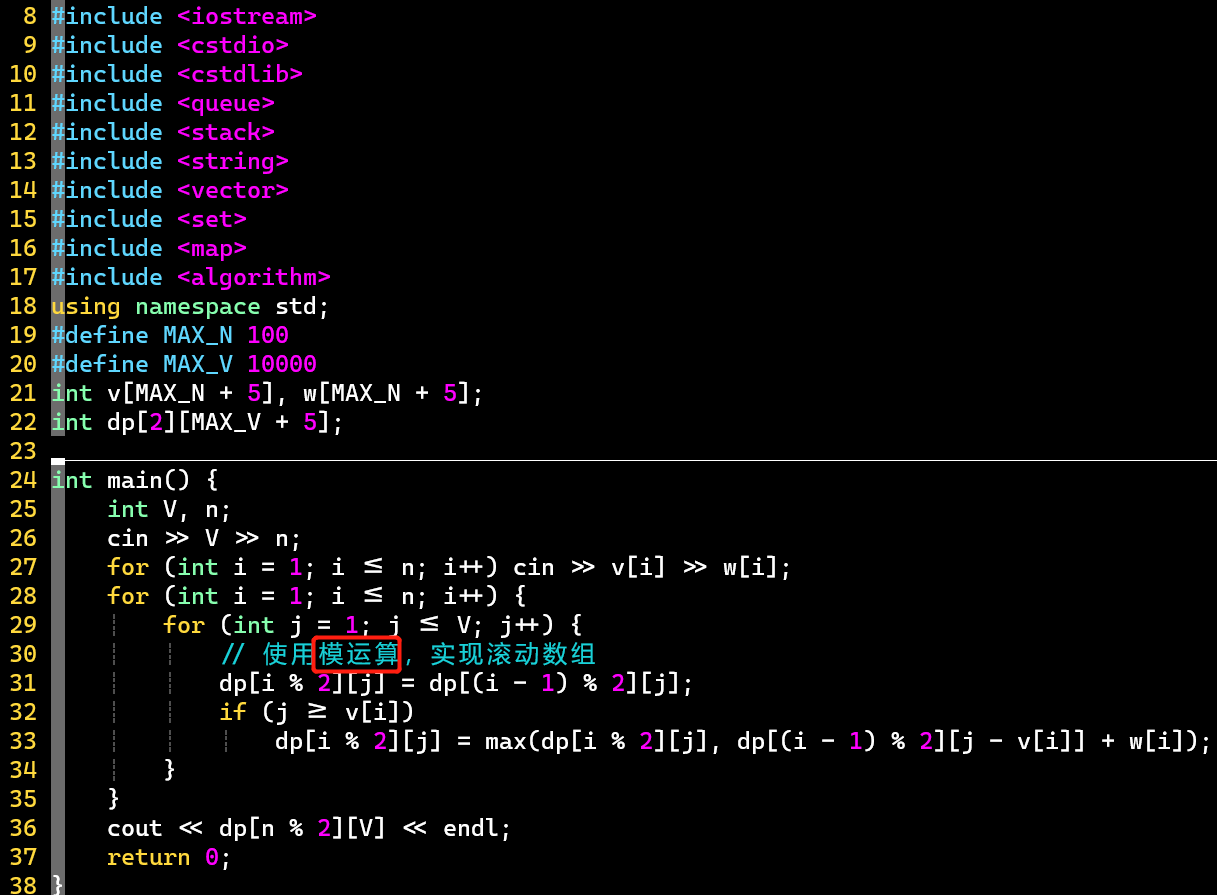
- i维度每次只使用当前行与前一行的值,所以只需要2维即可
- 在i维度统一模2即可
- ⭐V3:将程序中的dp数组变成1维,v、w数组变成0维,修改更新顺序
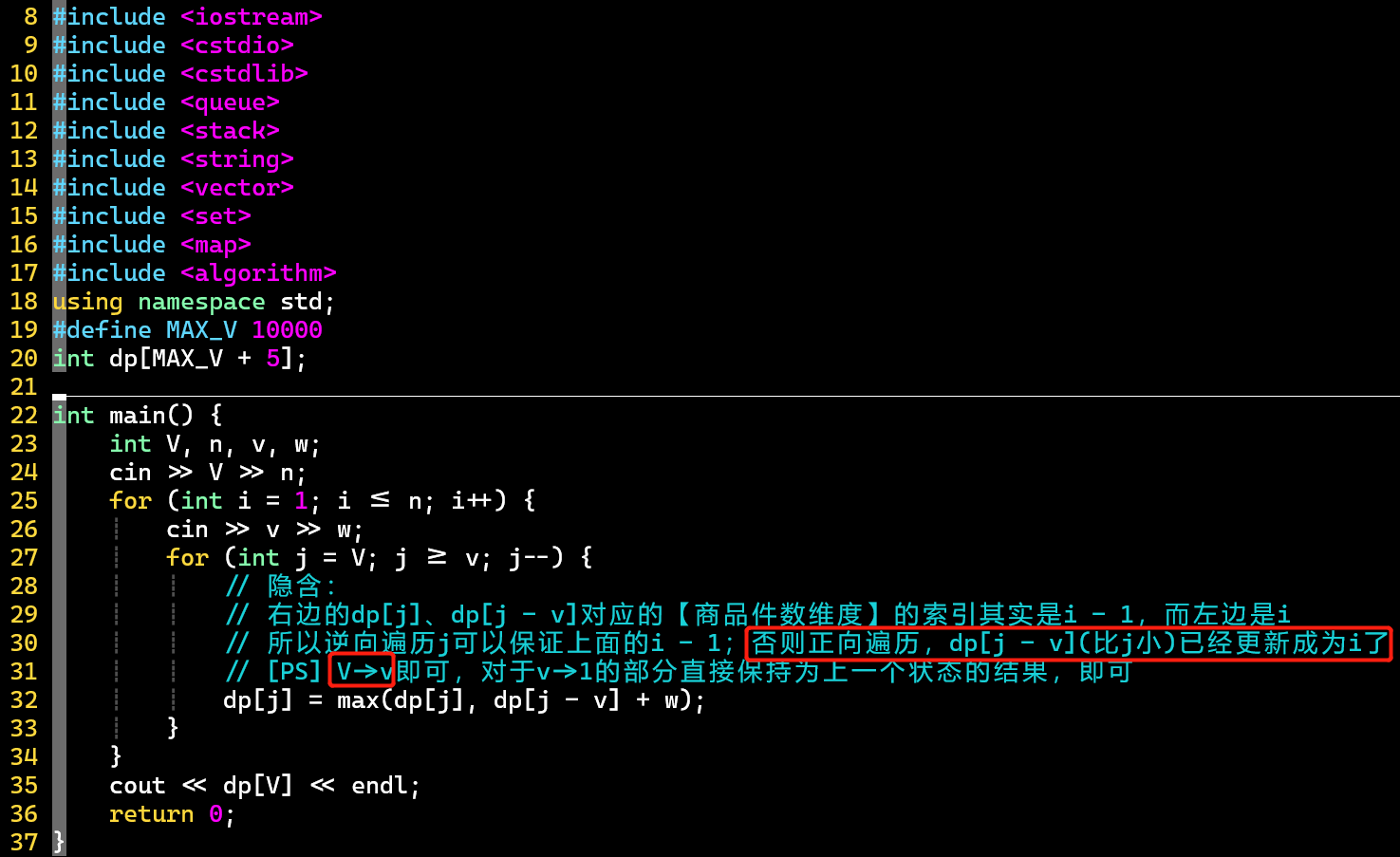
- 理解上述代码,需回答3个问题:
- ① 为什么dp数组只需要一维
- ② 为什么不需要v、w数组
- ③ 为什么逆序
- 解答:
- ① 思维还在,状态定义还是二维,只是代码实现上的优化
- ② 代表的是物品件数,从之前的代码可以看出,v、w只需关注第件物品,所以可以读入一件物品,处理一件物品
- ③ 首先理解第①个问题,状态转移代码要保证等式右边的在【物品件数】维度的索引为;如果正序,对应的索引已经变为 i 了,而已经丢失
- ❗ 这里j的遍历范围从之前的变成了
- 这是因为没遍历到的部分,其值不需要改变,保持即可 [dp是一维的]
- 而之前的代码也只是将维的值复制过来 [dp是二维的,否则为初始的0]
- V1:状态如何定义,程序就如何实现
HZOJ-48:完全背包
样例输入
5 20
2 3
3 4
10 9
5 2
11 11
样例输出
30
- 思路
- 状态定义 [类同0/1背包]
- :前 i 种物品,背包最大承重为 j 的情况下,能够获取的最大价值
- 状态转移
- ❗ 注意第二种转移状态,不管选了多少个第 i 种物品,物品种数还是前 i 种,因为每种物品有无数件可用,这是和上题最大的区别,有点像上面的钱币问题
- 这里腾出一个第 i 种物品的空间即可
- 时间复杂度:
- 状态定义 [类同0/1背包]
- 代码
-
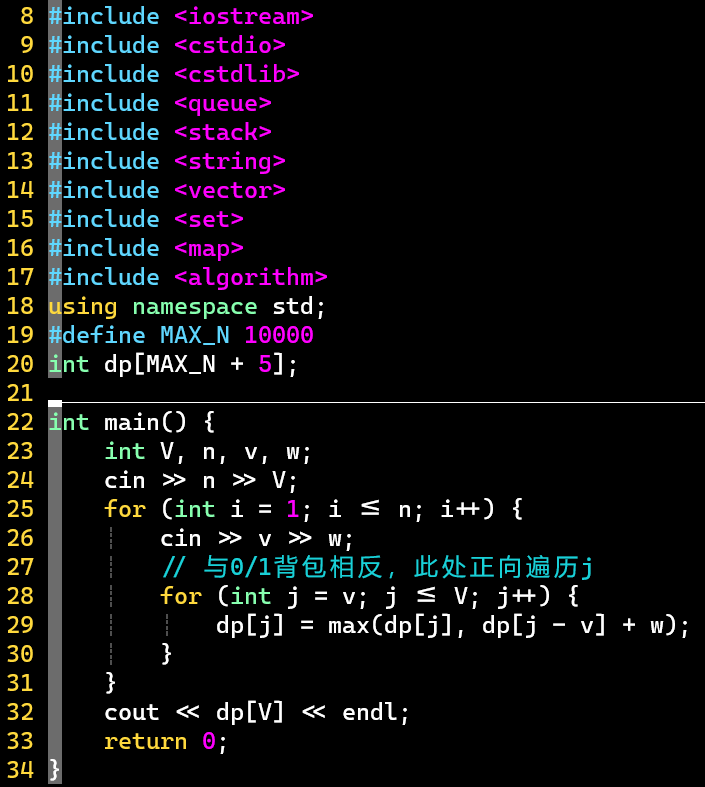
- 与上题0/1背包第3种实现方式的刷表顺序相反,需正向遍历 j,理解上文[❗]处即可理解此处
-
HZOJ-49:多重背包

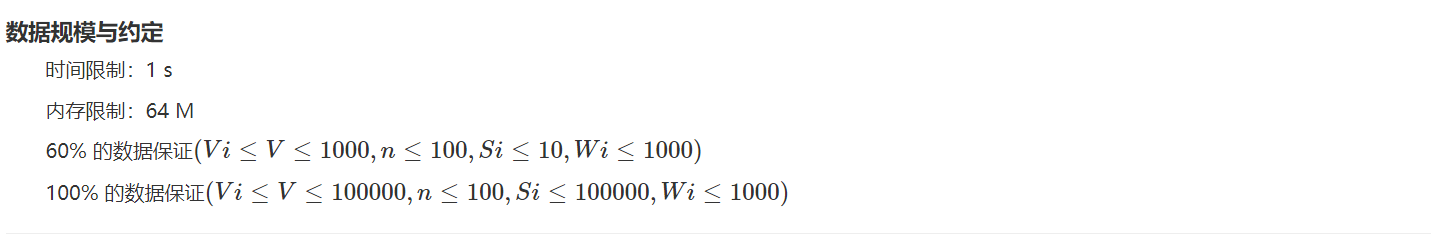
样例输入
15 4
4 10 5
3 7 4
12 12 2
9 8 7
样例输出
37
- 思路
- 普通版
- 🆒问题模型转换:把每种物品当成多个独立的一件物品来做,从而转换为0/1背包问题
- 状态定义与状态转移与0/1背包一致
- 状态定义
- :前 i 件物品,背包最大承重为 j 的情况下,能够获取的最大价值
- 状态转移
- 时间复杂度:,可优化
- 优化版——针对转移过程⭐
- 使用二进制拆分法,减少遍历相同物品的次数
- 本质上,对于某一类物品,需要我们决定的是具体选择多少件,才是最优答案
- 举例:1种物品有14件
- 普通的单一拆分法——需要14轮,依次枚举某个种物品选择件的所有情况
- 二进制拆分法——只需要4轮,将14件物品分成1、2、4、7件物品组成的四堆
- 可以达到相同的效果,并且拆分出来的数量会更少
- 每次拆分的数量是上一堆的两倍,不够拆了就放剩下全部的即可
- 拆分件物品的份数比较:普通拆分法:份;二进制拆分法:份
- 时间复杂度:
- [PS] 只能用二进制拆分
- 对于每堆物品,只有选与不选两种状态,因为在转移过程中,也只有转与不转两种结果
- 所以无法用其它进制
- 最优时间复杂度:——借助单调队列,后续再讲
- 普通版
- 代码
- V1:当成0/1背包问题来做
-
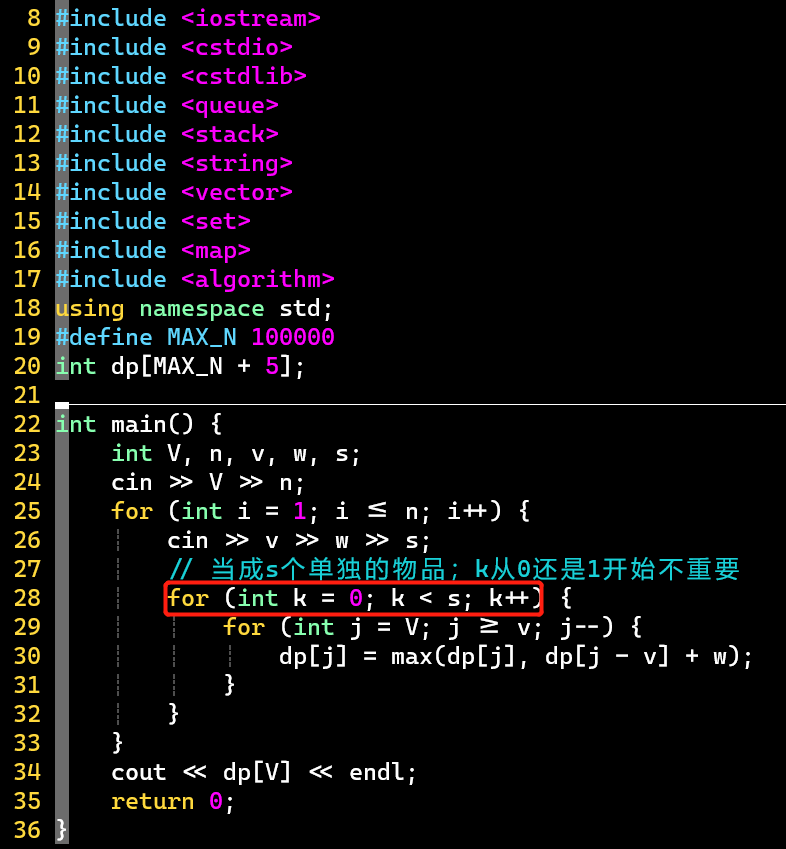
- 时间效率不高
-
- V2:优化转移过程
- 利用二进制拆分法
-
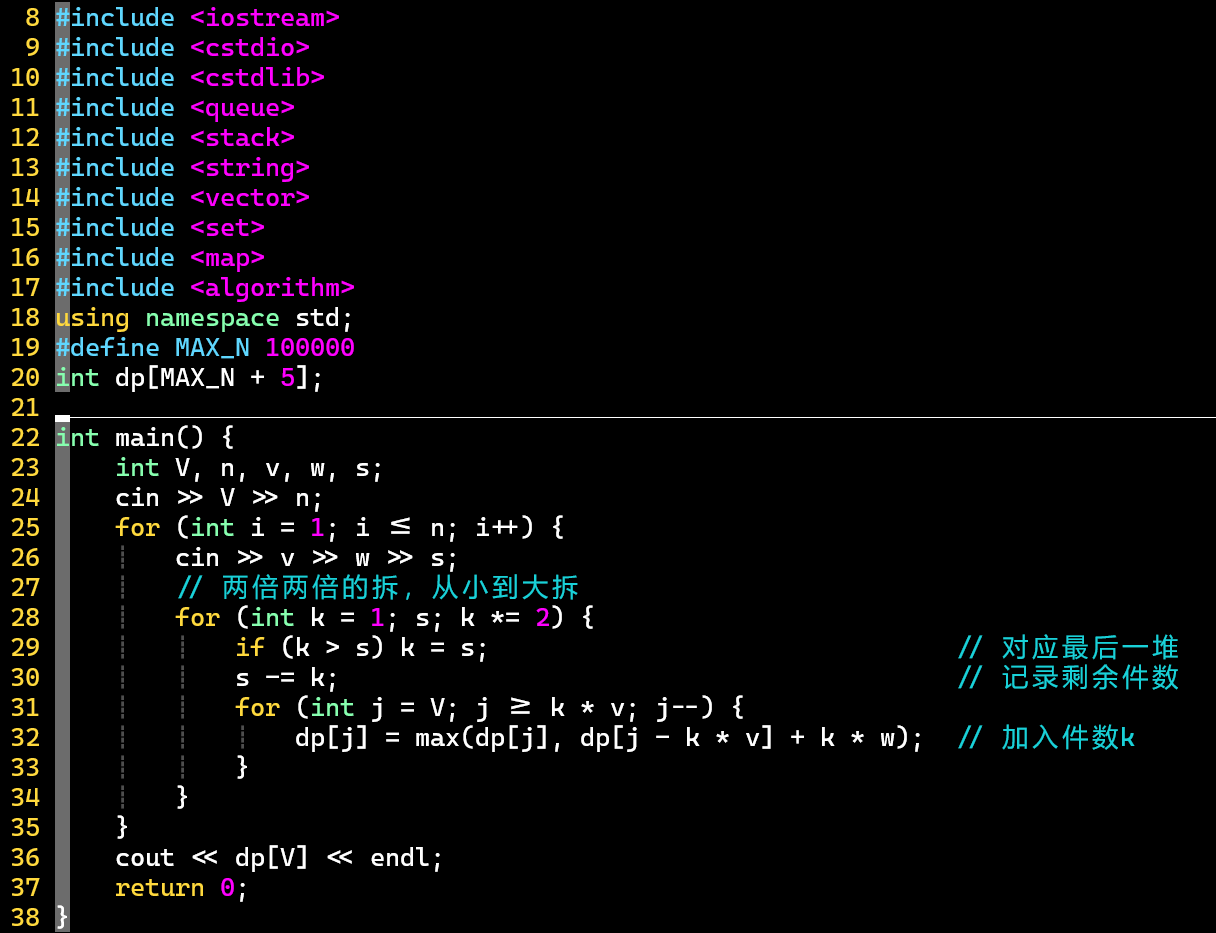
- 两倍两倍、从小到大地拆,才能遍历全部情况
- 在转移方程中考虑件数
- V1:当成0/1背包问题来做
HZOJ-50:扔鸡蛋

样例输入
2 100
样例输出
14
- 思路
- 【探索思路】
- 解读所求:最坏情况下最少测多少次
- 测试次数,与测试方法有关
- 最坏情况,表示测试过程中,运气是最差的
- 👉 最好策略、最坏运气
- 举例:2个鸡蛋,楼高为100
- 二分方式:肯定超时,鸡蛋数量有限
- [最坏情况]
- 第一个鸡蛋测楼高50,碎了
- 第二个鸡蛋只能从第一层楼乖乖往上测
- 最终需要测50次 [最坏情况→硬度是49]
- 自定义策略:以10层为间隔往上测
- [最坏情况]
- 10、20、30、...、100,在100时鸡蛋碎了
- 再91、92、...、99
- 最终需要测19次 [硬度是99]
- 假设测试次数是x次
- [最坏情况,敢测试的楼层数如下,保证测试次数是x]
- 第一次:
- 第二次:
- 第三次:
- 最后:,加到1是为了能测的楼层最多,即最优策略
- 计算等差数列和:时的x值,等于14
- 可知:2个鸡蛋测100层楼,最多最少测14次
- 二分方式:肯定超时,鸡蛋数量有限
- 启发:固定测试次数的情况,发现测试策略
- 解读所求:最坏情况下最少测多少次
- V1:普通版
- 状态定义
- :用 i 个鸡蛋,测 j 层楼,最坏情况下最少测多少次
- 状态转移
-
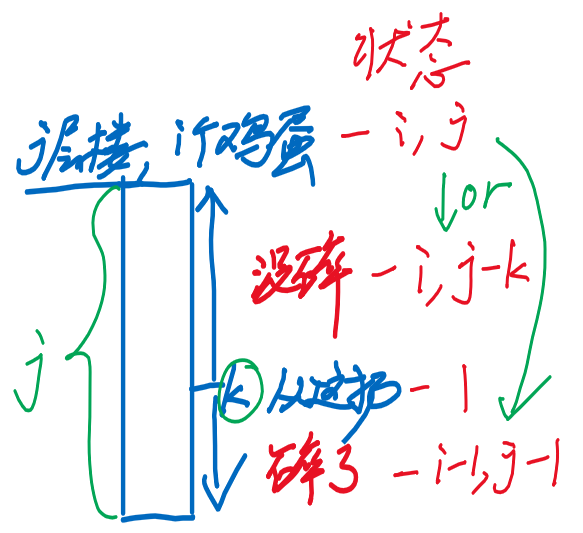
- k:从k楼扔鸡蛋
- max:运气最差
- min:最少测试次数 [枚举所有的k,取最小值]
- 决策:体现在两种状态中取最大值,所有楼层对应的结果种取最小值
-
- 该方法思维正确,但存在明显的空间和时间限制,详见代码——V1
- 状态定义
- V2:优化转移过程
- V1版本中有3层循环,而针对遍历求min的过程进行优化,可以转为2层循环
- ① 固定鸡蛋数、楼层数,观察与、之间的关系
-
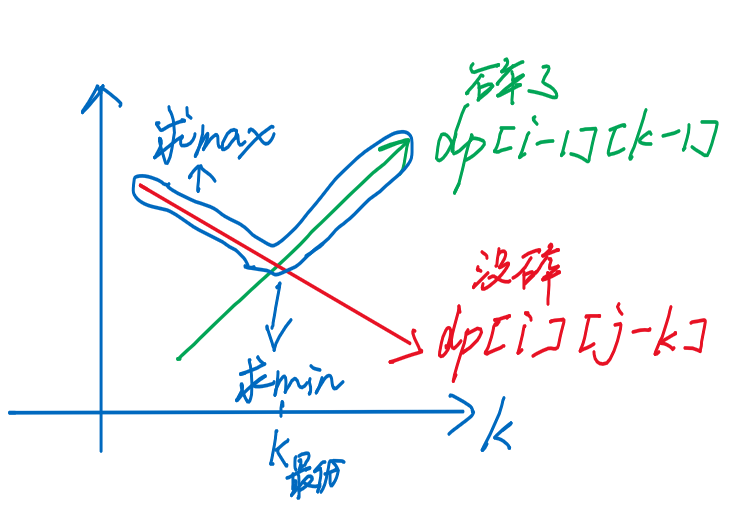
- 前者与正相关,后者与负相关
- 而要求min(max()),如图所示,就是两者取max后值找min,所以两者相交的地方,就是最优的k值
- 👉 最优的转移k值,一定发生在两个函数的交点附近[PS:k的取值是离散的]
-
- ② 固定鸡蛋数,再观察楼层数与最优的的关系
-
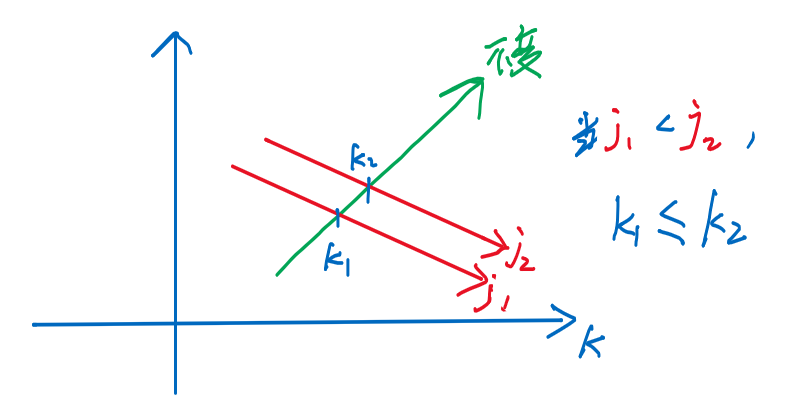
- 当楼层数增大时,绿线不受影响,红线整体上移,最优的值也会上移
- 准确说,至少不会变小,因为k值是离散的,楼层数增大一定范围时,才增大,总次数才会有增大 [k对应的曲线是阶梯的]
-
- 综合两条结论
- 假设对应的最优解为,则对应的最优解[一定]
- 并且仍需满足条件[①]
- 若满足,一定是满足该条件的最大值,因为最多加一
- 所以,增加一层楼层,要么加一,要么不变【⭐】
- 如果代入条件[①]成立,则
- 假设对应的最优解为,则对应的最优解[一定]
- 本质优化的是求min的过程,时间复杂度已经有了质的飞跃,详见代码——V2
- V3:优化状态定义
- 状态重定义
- 令原状态定义,代表最少最多的测试次数
- 分析:原状态定义所需存储空间与楼层数相关,而的值域非常大,数组存不下;反观,的值域小,如时,[根号关系]
- 技巧:当发现某个自变量与因变量之间存在相关性时,两者可对调
- ⭐重定义:,个鸡蛋扔次,最多测多少层楼
- 状态转移
- 所能测的最大楼层数 = 上 [没碎] + 下 [碎了] + 1
- 注意:dp数组元素代表的含义已经变为楼层数
- 此时已不是一个动态规划问题了,而是递推问题,没有决策
- 最后找第一个使[所给楼层] 对应的方法数,即答案
- 🆒最终解决了V1版本的空间和时间限制
- [PS] 如果值域相差不大,转换就没有意义;找不到相关的变量,也没法转换
- 状态重定义
- 注意:所有转移公式都是针对鸡蛋数至少2个的情况,所以记得初始化1个鸡蛋的情况
- 【探索思路】
- 代码
- V1
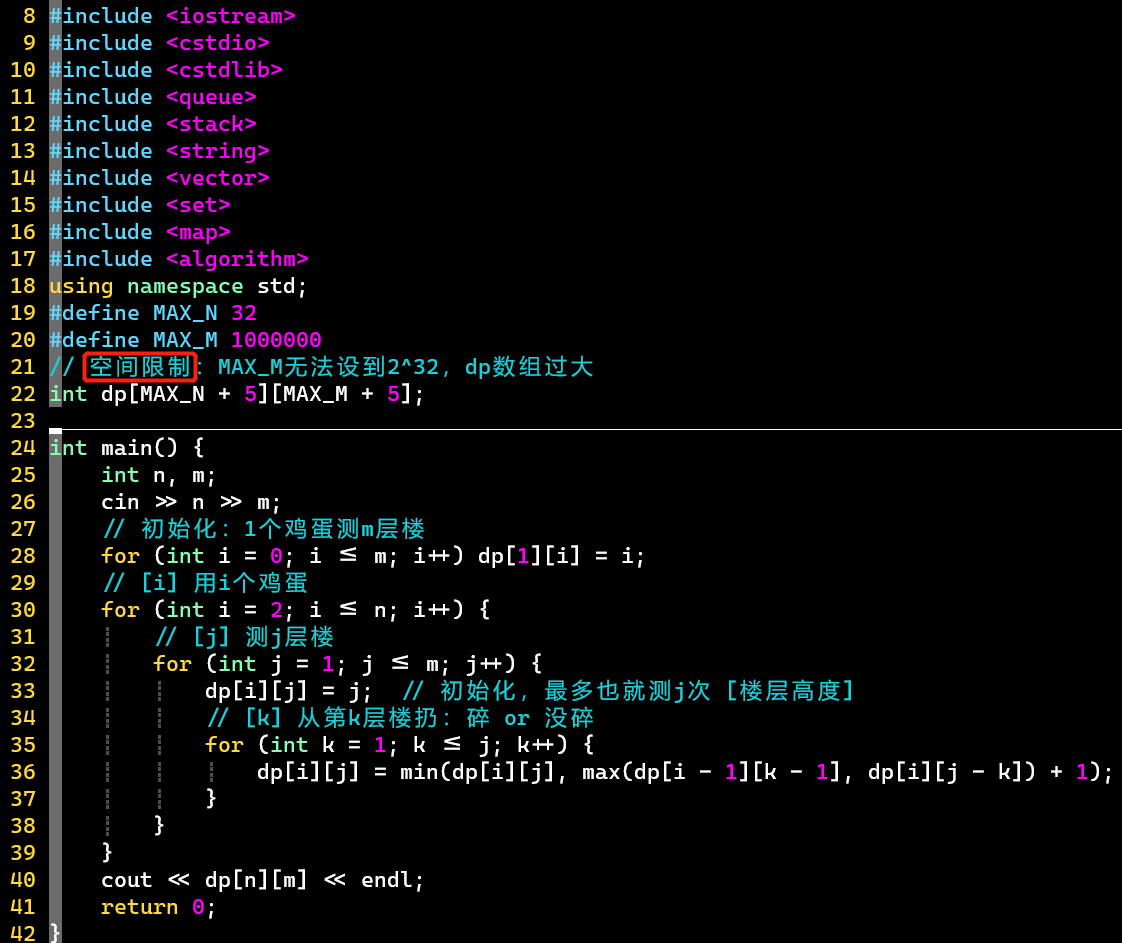
- 对于在一个范围内求最值的情况,一般需要初始化一个极端值
- 空间限制
- 此程序所使用的存储空间与楼层数量强相关
- 而楼层数量达到了,所以这种状态定义不能满足需求
- 👉 需要优化状态定义
- 时间限制
- 时间复杂度:
- 当m过大时,时间消耗很大
- [PS] dp数组第一维可以压缩,利用滚动数组,但第二维压缩的突破口不在此
- V2:转移过程优化
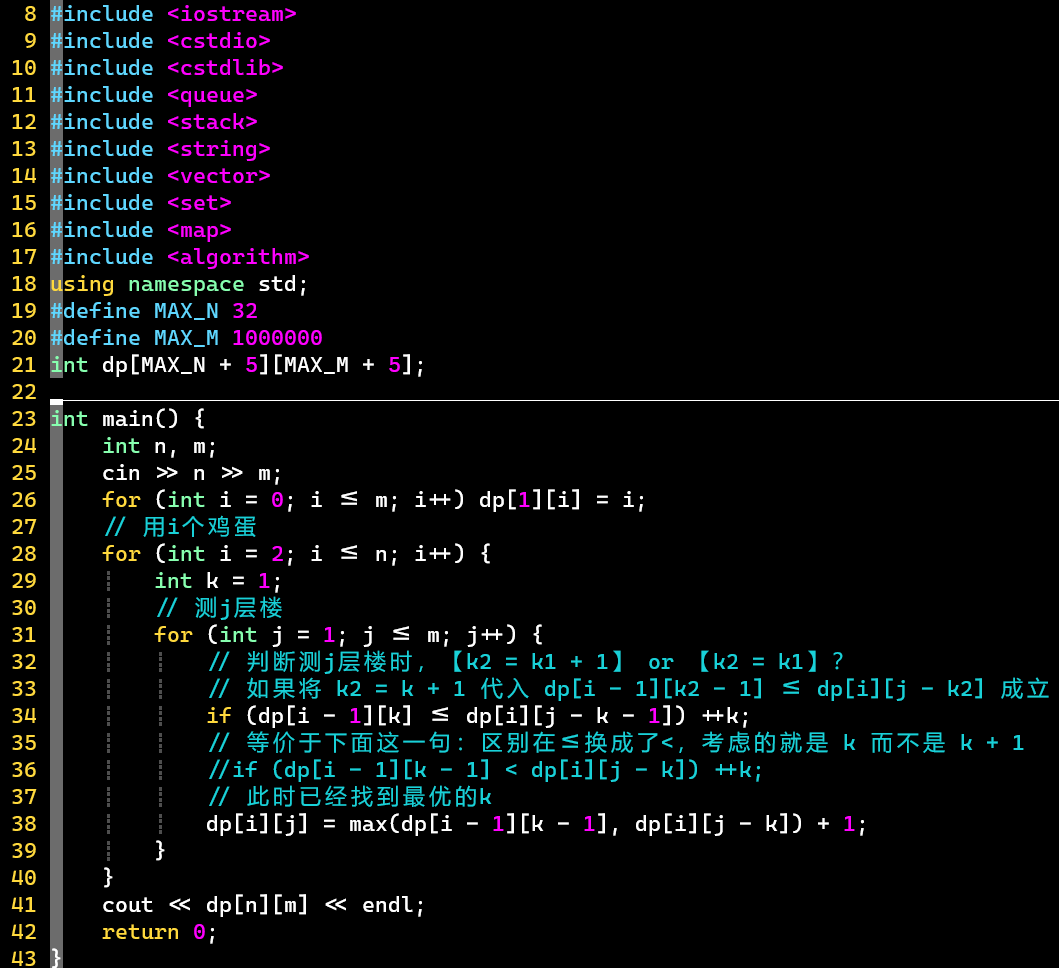
- 【关键】根据拐点结论,判断此时鸡蛋数、楼层数对应的最优的是否可以+1
- 时间复杂度 ->
- [个人思考] 这里拐点结论其实如果是满足的最小值也是可以的(令该值为,相比的最大值,),因为两者的曲线(阶梯状)是对称的(因为第34行若换成,在OJ上是同样的效果),所以猜测若,的同时,,所以所求的答案不变
- 事实上确实是对称的,可用数学归纳法证明
- V3:状态定义优化
-
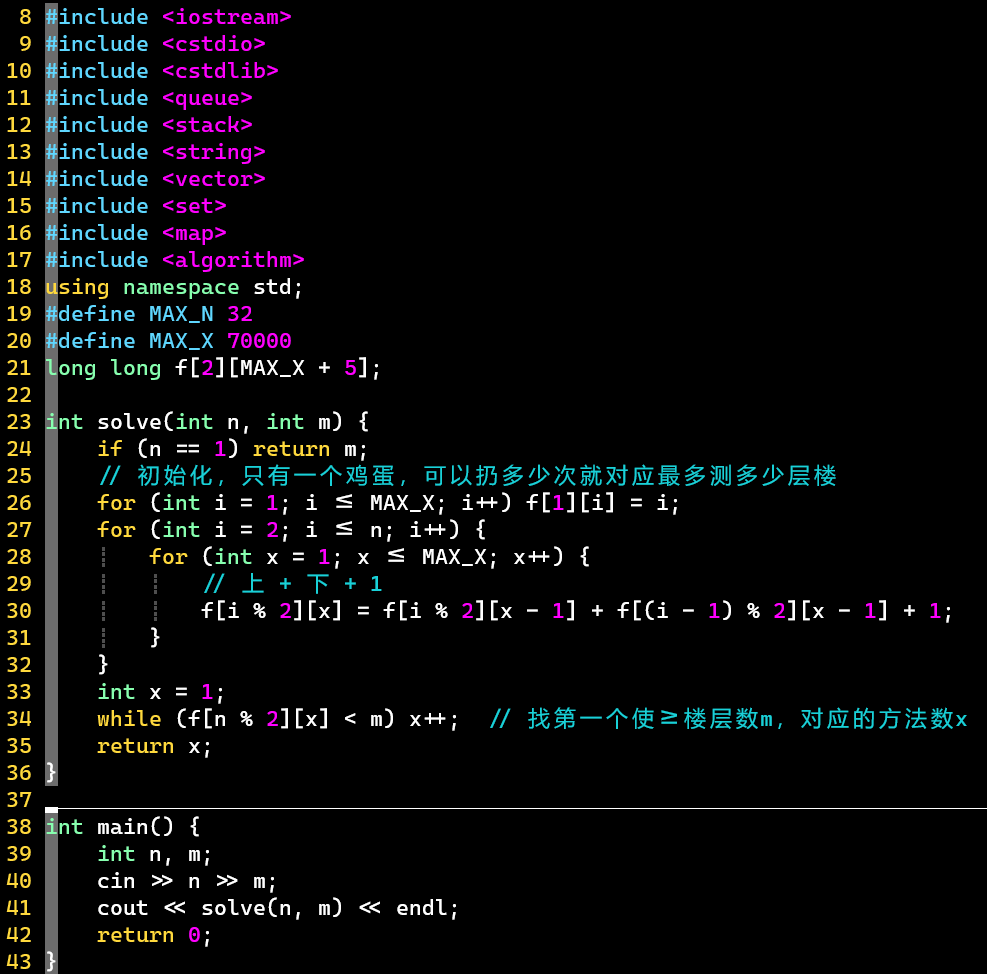
- 已转变为递推问题,dp[][]->f[][]
- f 数组使用long long类型,虽然楼层数最高为,在int范围内;但鸡蛋数最大为32,对应楼层数超过int,可能会发生未定义行为
- f 数组第二维大小设到了70000,因为鸡蛋数为2,楼层数为时,对应的x值为
- 程序优化:改成滚动数组存储;可根据楼层数估计 f 数组第二维大小,动态开辟数组,因为不需要每次开70000那么大
- [PS] 也可使用递归+记忆化实现
-
- V1
HZOJ-44:最长上升子序列

样例输入
10
3 2 5 7 4 5 7 9 6 8
样例输出
5
- 思路
- 普通版
- 能够挑出来的最长严格上升子序列[不需要连续挑]
- 状态定义
- :代表以索引为i的元素结尾的最长严格上升序列长度
- 必须以 i 结尾!
- 状态转移
- 所有能够转移到的状态:满足条件的,共 i 个
- 决策:
- 最终答案:,在所有的中取最大值
- 状态转移的时间复杂度:
- 优化版——转移过程
- ⭐增加一个数组,代表长度为的[严格上升]序列中,末尾最小值
- 状态转移
-
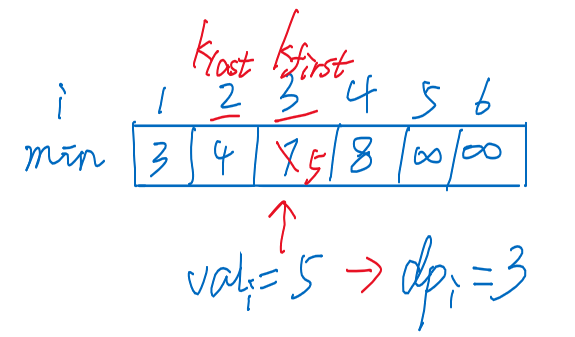
- 引入
- 参照上图的数组,实际上,代表长度,代表末尾最小值
- 思考:当有一个新的时,其接在数组中哪个值后最佳?
- ① 首先需要满足序列末尾值比它小 👉
- ② 然后序列长度越大越好 👉接入的位置越大越好
- 转换:在数组中找最后一个小于的值的索引,再+1即得接入位置;并更新的值为,因为更新前是一定成立的,否则就不是最后一个
- 即:,涉及特殊二分11110000
- 实际上等价于找第一个大于等于的值 👇
- ,涉及特殊二分00001111,再更新即可
- 更简洁,后面代码也是这样实现的
-
- 可以二分的前提条件是数组的单调性
- 证明:数组一定是单调的,即证明
- ① 初始是单调的
- 初始的时候设置为0,∞,∞即可
- ② 假设更新前是单调的,更新后还是单调的
- 更新操作:
- 更新前:
- 更新后:
- 所以,单调
- 时间复杂度:
- 代表最长上升子序列的长度,即答案,也是数组的最终有效长度
- 使用了二分查找优化转移过程
- 【关键】维护了一个单调数组,该数组与所求强相关,实际是使用二分优化
- 普通版
- 代码
- 普通版
-
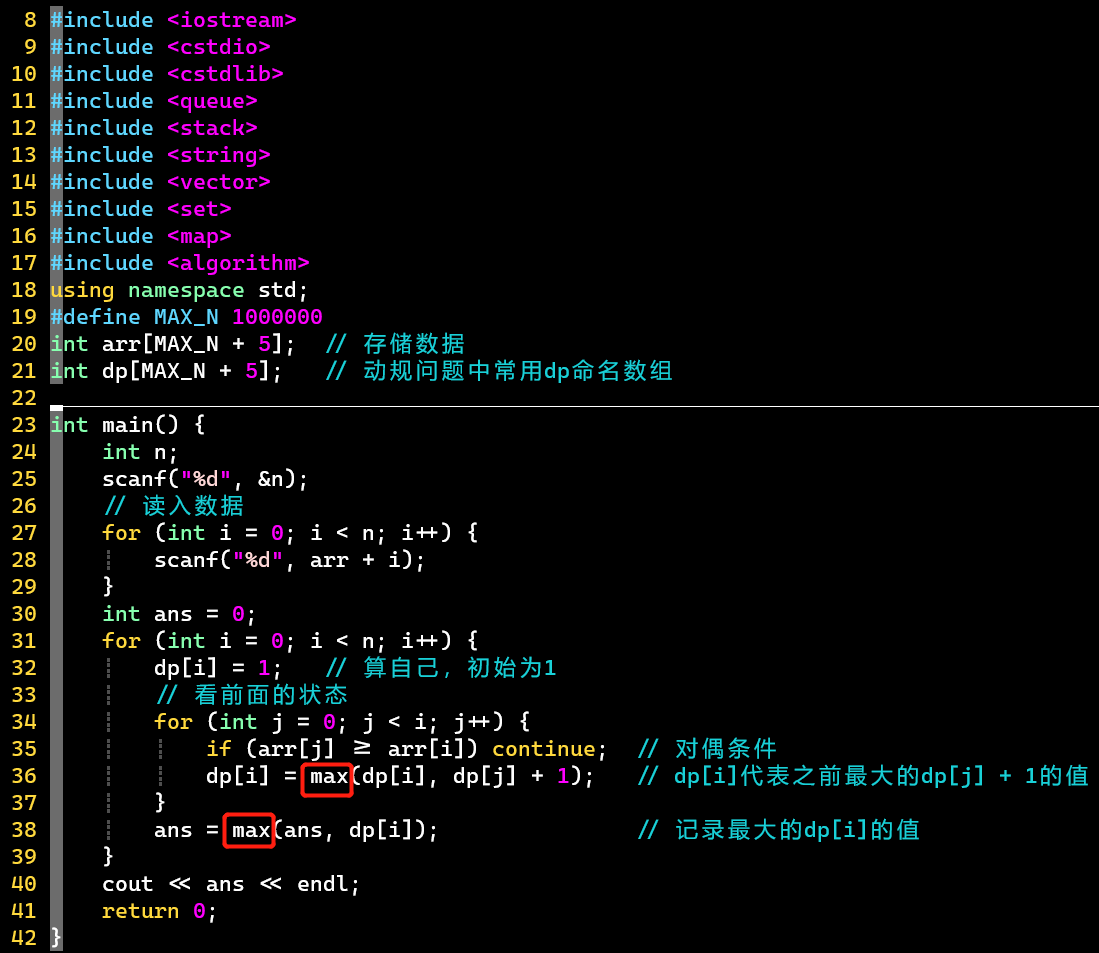
- 数据很大,使用scanf,而不是cin
- 注意两个max的含义
- 状态转移的时间效率低
-
- 优化版——状态转移
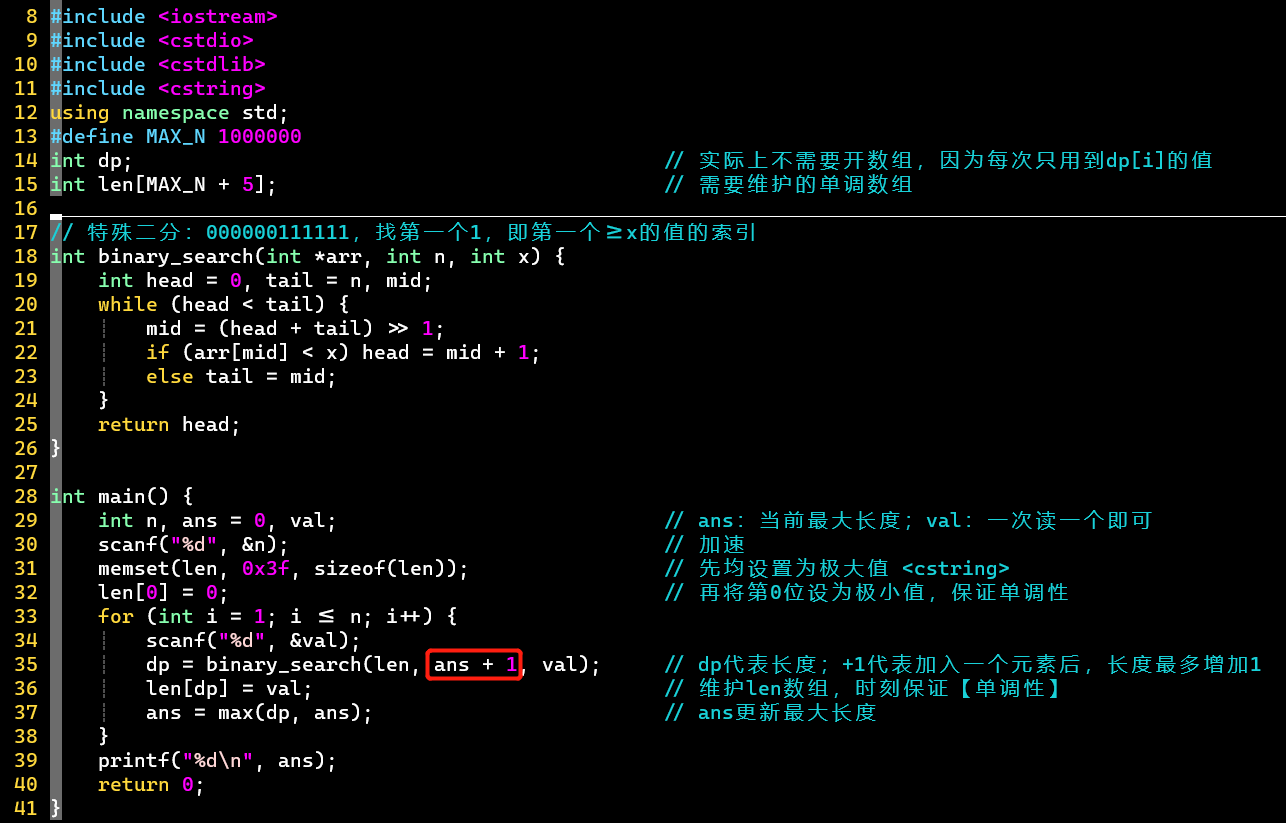
- 注意单调数组的维护,以及特殊二分0000011111
- 二分查找时,ans + 1代表每加入一个元素,最大长度最多+1
- ans代表len数组中最后一位非极大值的下标,也是当前序列的最大上升子序列最大长度
- [PS]
- 不需要开dp、val数组,每次只用到当前状态的值
- 使用memset设置无穷大操作:为何程序员喜欢将INF设置为0x3f3f3f3f——知乎
- 普通版
——结合单调队列/栈——
基于3 单调栈与单调队列的知识点
HZOJ-51:矩形
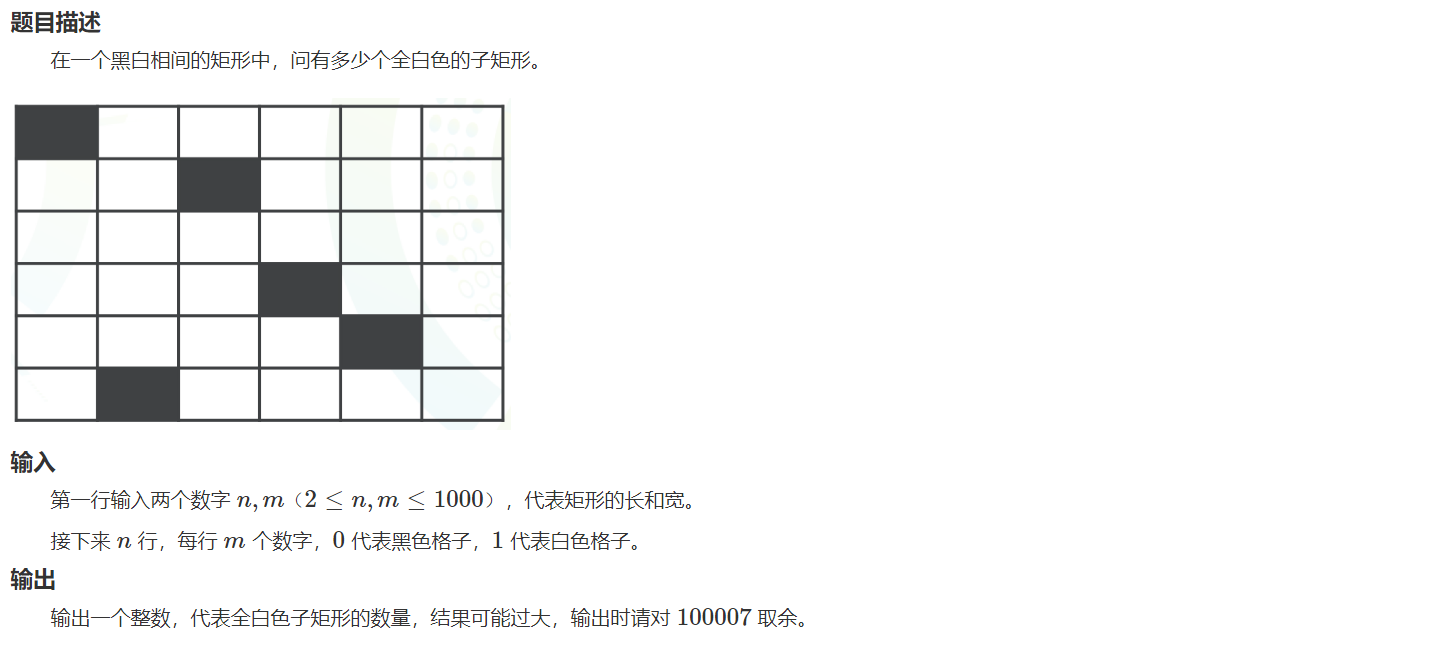
样例输入
6 6
0 1 1 1 1 1
1 1 0 1 1 1
1 1 1 1 1 1
1 1 1 0 1 1
1 1 1 1 0 1
1 0 1 1 1 1
样例输出
152
- 思路
- 递推+ 单调栈
- 注意:结果可能过大,输出时对100007取余
- 【常识】左上角坐标 + 右下角坐标 👉 唯一的1个小矩形
- 问题转换:先针对一行,右下角坐标落在该行某一点上时,求能构成的合法子矩形数量 [该点对应几个合法的左上角坐标,就有几个子矩形];再累加所有点的数量即可
- 通过观察,将上述子问题再变成两部分子问题
-
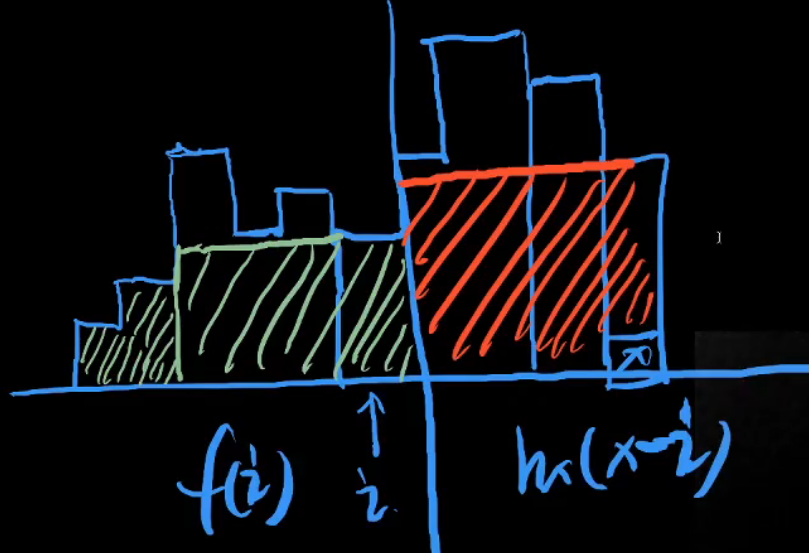
- 首先找到左侧离点最近的,小于高度 [向上数连续白色格子的数量] 的位置
- 则【状态定义】以作为右下角坐标所能构成的合法子矩形数量满足 👇
- 【递推公式】
- 能以点作为右下角的子矩形数量,对应合法左上角坐标数量,而这些坐标一定也可以作为点的合法左上角坐标
- 即:左侧部分合法的矩形个数➕ 右侧部分合法的矩形个数
- 因为需要求解的最近小于值,所以要用到单调栈
-
- [启发] 在有查找最近大于小于值的需求,应该想到单调栈 [一般是与其他算法结合]
- 代码


- 需要使用数组的地方:单调栈、矩形高度、递推状态
- 注意:留虚拟木板、初始化递推状态值、初始化栈底
- 常规的单调栈套路:维护单调性→取值→入栈
- [PS] 取两次余:可防止未取余的与相加超范围,实际上该题不会超;此外,并不能防止超范围 [如果发生],因为已经计算完了
HZOJ-52:古老的打字机

样例输入
6 40
3 3 6 5 1 2
样例输出
256
- 思路
- 动态规划+ 单调队列
- 状态定义:代表打印前个字符的最小消耗值
- 状态转移
-
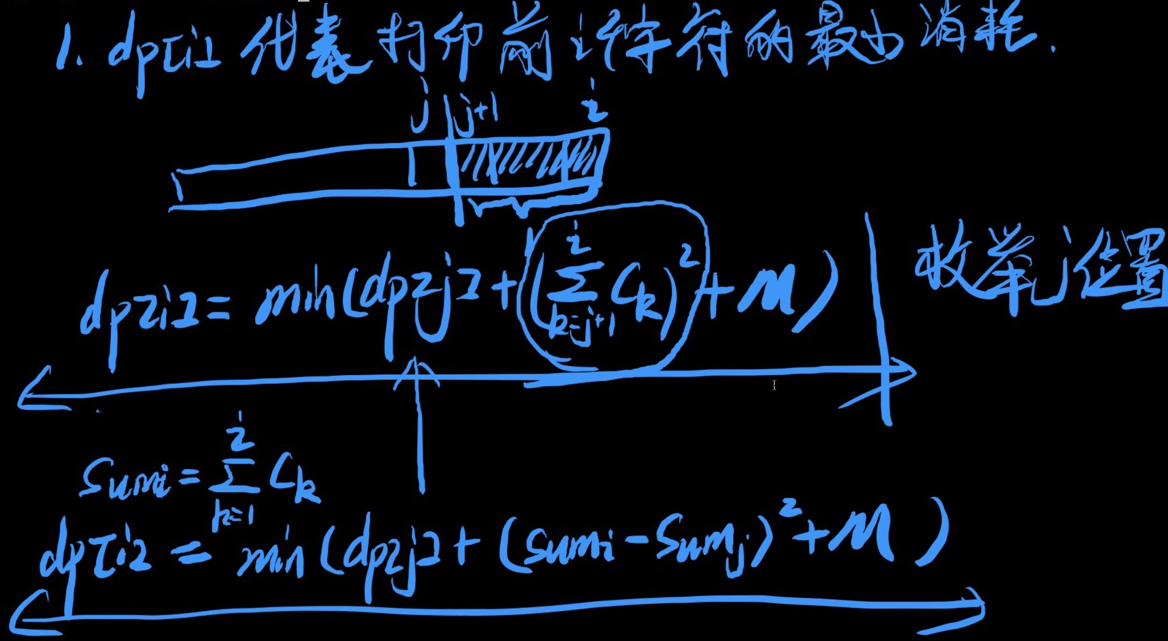
- 根据题意:,其中为前缀和
- 枚举上一段打印的可能终止位置,找最优
- 时间复杂度:
-
- 斜率优化 [⭐特别优美一类优化算法]
- ① 分析状态转移公式 [消耗值公式] 的组成
-
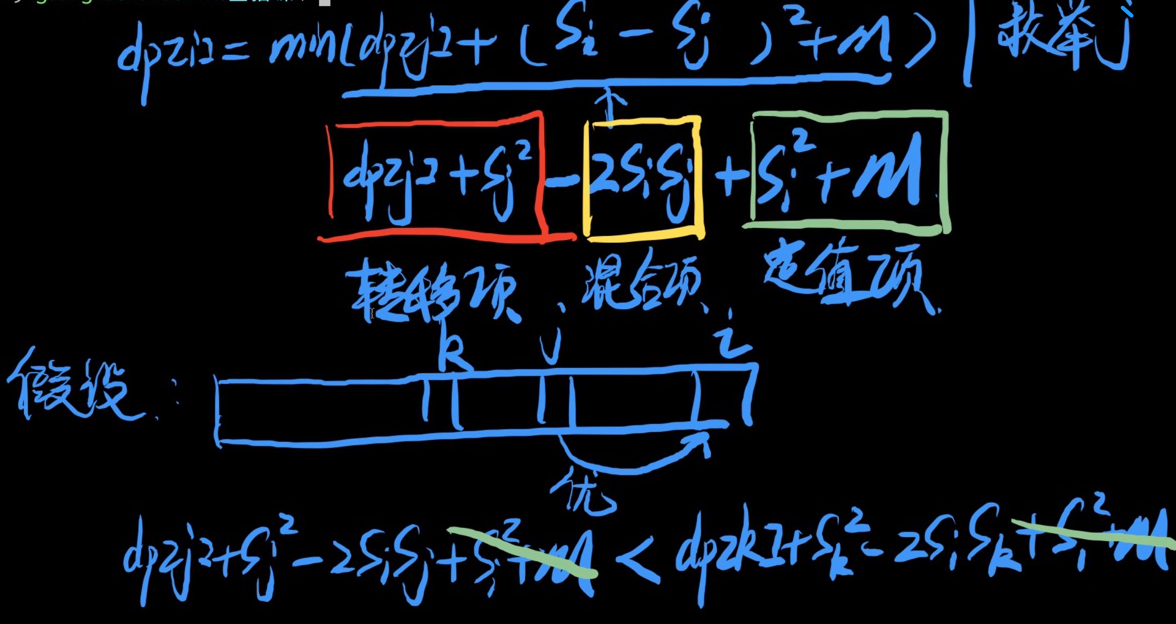
- 主要是干掉混合项
-
- ② 我们实际上要找的是从哪个状态转移更优秀。假设从转移要优于从转移移,即消耗值更小,则
- ↓
- ↓
- ↓
- ③ 进一步转换,变成斜率的模样
-

- 令
- ↓ 【斜率关系(Ⅰ) 】
- 👉 斜率 [将当成横坐标、当成纵坐标]
- 此时转换为:如果斜率关系(Ⅰ)成立,则从转移比更优秀
-
- ④ 如何进一步利用斜率关系(Ⅰ)呢?分析如下图所示,有、、三点
-

- 【此处场景】直线的斜率 > 直线的斜率 [弓背型]
- 分析两者斜率与的关系,有三种情况,见图中①、②、③
- 再由斜率关系(Ⅰ)分析:选择从哪点转移最优秀,见九宫格✔处
- 可见,能成为最优状态的一定没有
- 👉 备选答案中,一定没有弓背型
-
- ⑤ 最终这个过程转换为:保证候选状态之间,前者斜率一定小不大后者 [非弓背型]
-

- 根据斜率关系(Ⅰ)和斜率递增的特点,所求的最优转移状态靠近头部
- 首先根据斜率关系(Ⅰ)删除头部相关元素、 【出队】
- 此时剩下的最左边元素即最优转移状态【队首】
- 当有新的状态加入时:根据弓背型原则先剔除掉队尾的非备选状态、,再加入【维护单调性 + 入队】
- 👉 即维护一个【单调队列】,维护一个区间最小值
-
- 时间复杂度:
- ① 分析状态转移公式 [消耗值公式] 的组成
- 代码
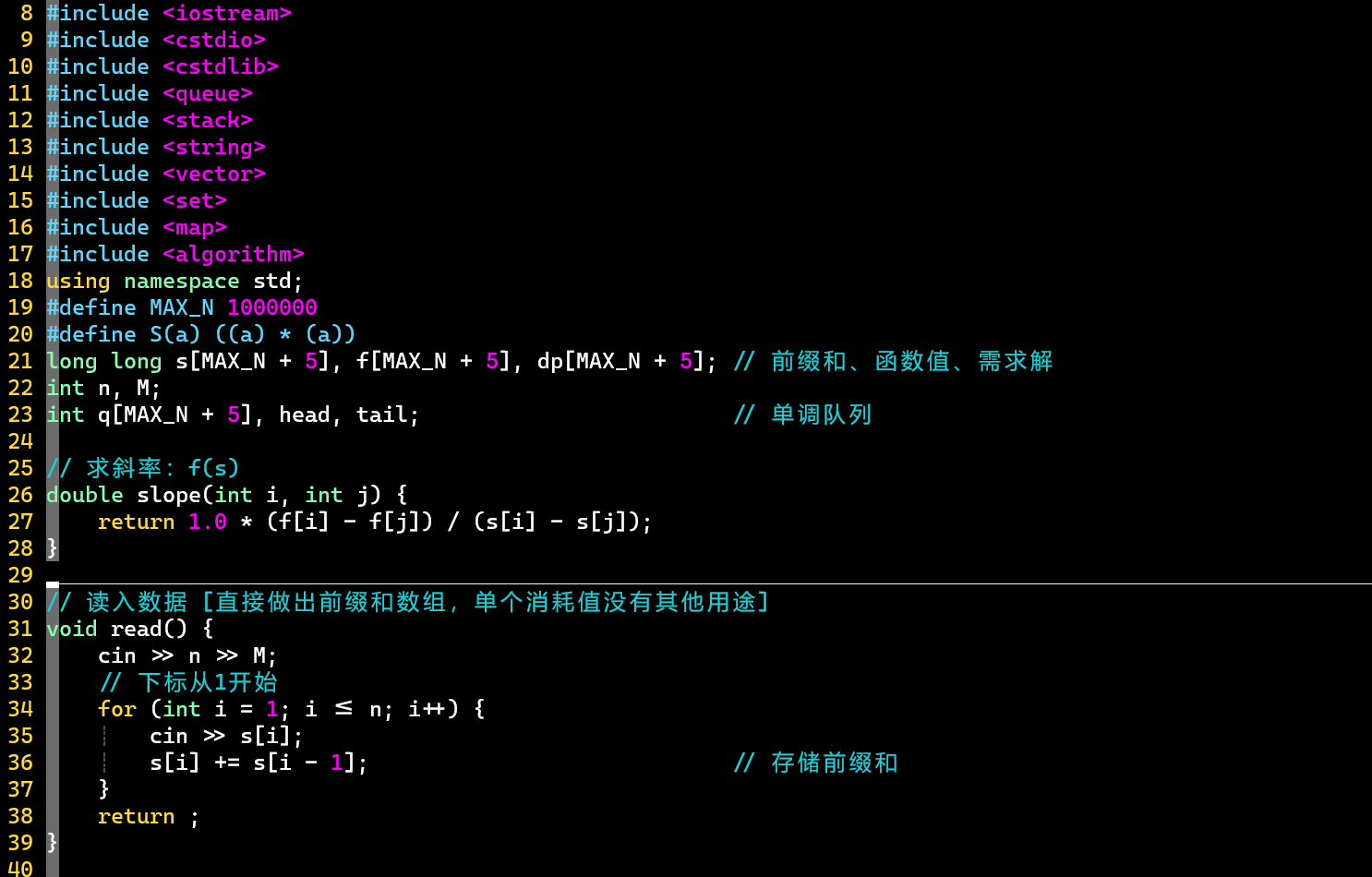
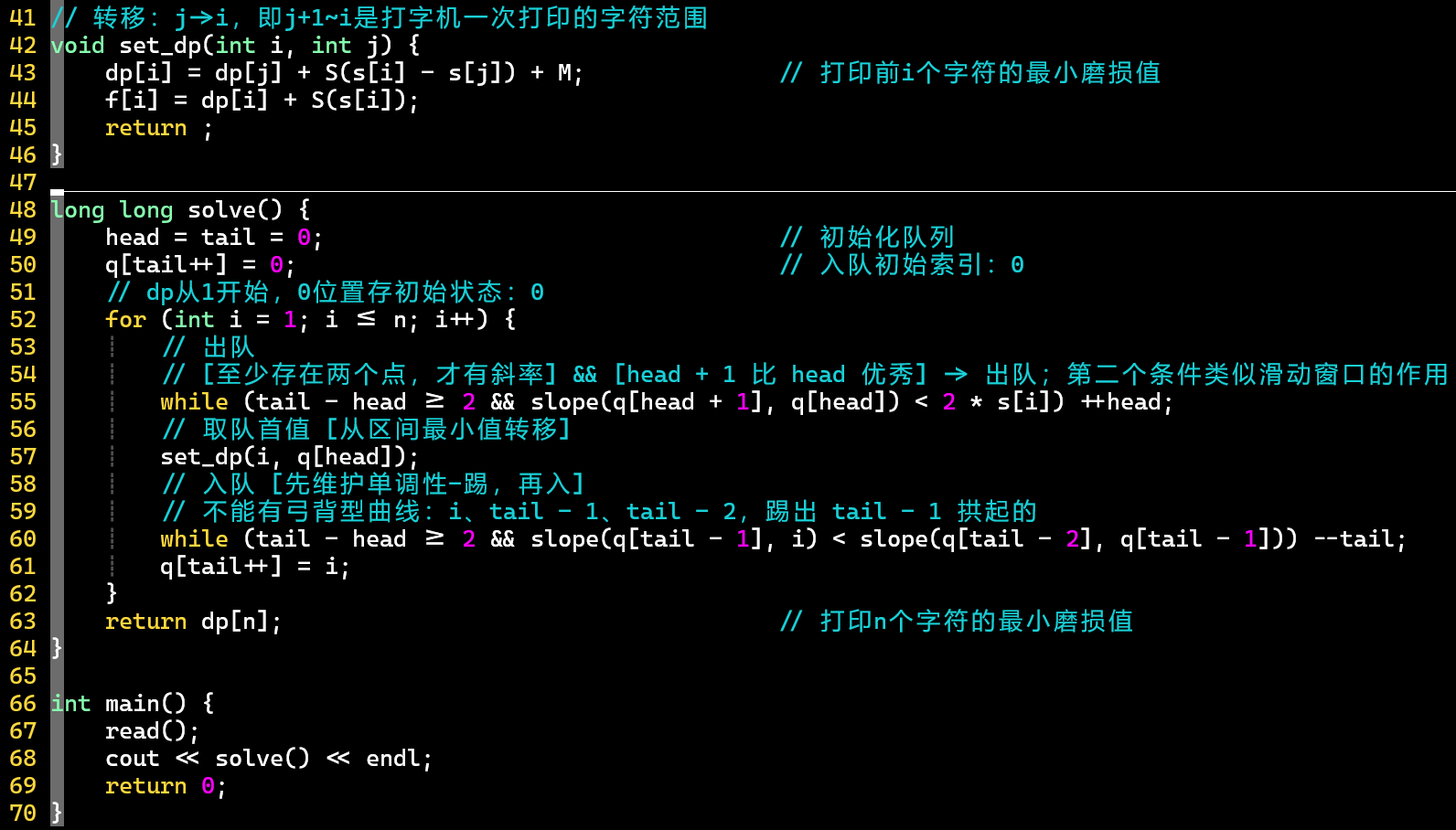
- 关键在于斜率优化的思想,注意运用斜率关系(Ⅰ)公式和斜率比较 (弓背型判断)
- 转换为单调队列的问题:出队→取值→维护单调性→入队
- 先后顺序根据题意调整
- [PS]
- 有了斜率优化的思想,根据公式生搬硬套即可
- 单纯存字符消耗值的数组没有存在的必要,只需要前缀和信息
Tips
- 知识本无界,有了大学,就有了界


