课程内容
问题引入
- 函数:查询数组区间内部的最小值,参考RMQ——OI Wiki
- 如果固定询问区间的尾部,例如:
- 最少记录如下4个蓝色元素,即可满足的所有需求
-

- 并且这4个元素构成了一个单调递增的序列,也是单调队列
- 单调队列解决的就是这类维护区间最值的问题 [固定结尾的RMQ问题]
单调队列
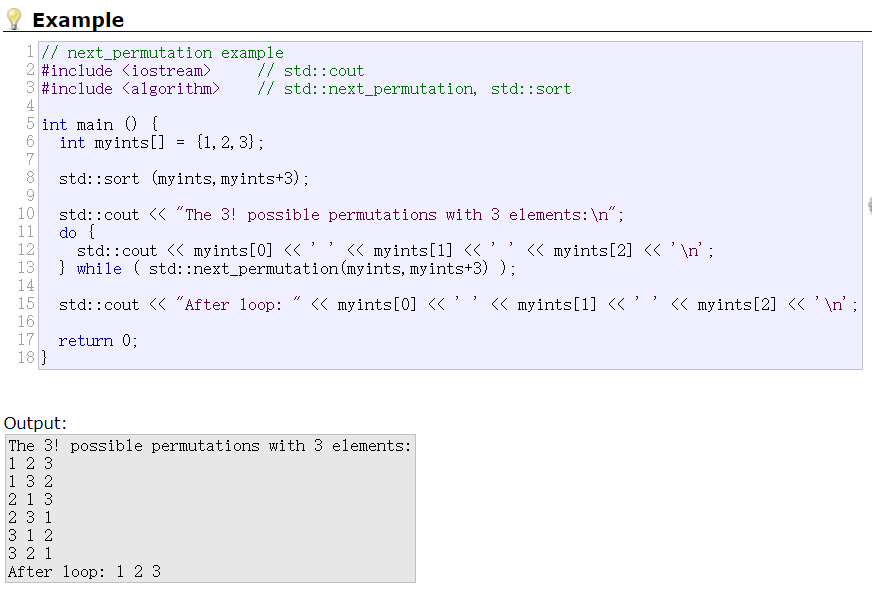
- 要解决的问题性质:维护滑动窗口内部的区间最值
- 结构定义:单调的队列
- 结构操作
- 入队:先将队尾违反单调性的元素淘汰出局,再将当前元素入队
- 出队:如果队首元素超出了滑动窗口的范围,队首出队
- 维护的核心:队首元素——滑动窗口内的最值⭐
- 最小值→递增队列
- 最大值→递减队列
- 均摊时间复杂度:O(1),求解一次
- [PS] 再举个例加深印象:学校选出学生代表去参赛
-

- 类比:年级->数组索引,能力值->数据值,时间段->滑动窗口
- 在维护区间[14-17]最大值的单调队列中,当你入队时,赵六就会被踢出
- 延伸:如果一个人年龄比你小,能力还比你强,那你就永远被踢掉了
-
单调栈
- 想想栈和队列的区别,而单调栈和单调队列的唯一区别也就在这,其它操作一致 [入队、出队]
-
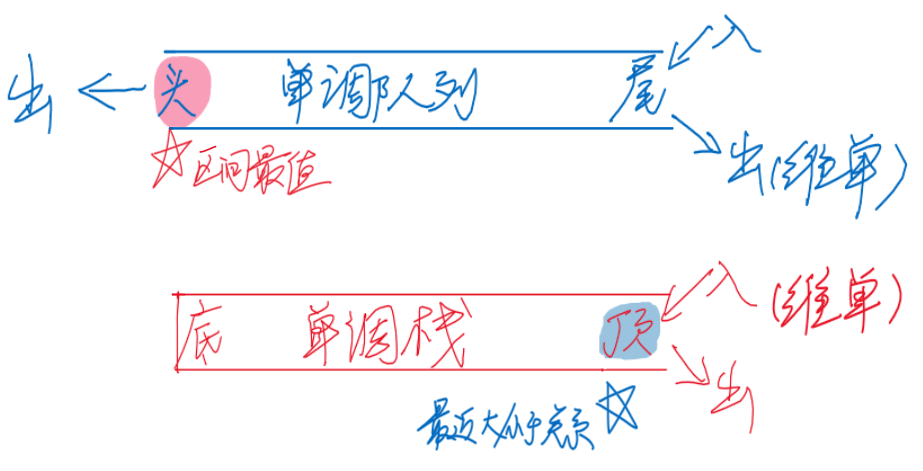
- 单调栈是一头堵死的单调队列
- 单调栈保留了单调队列的入队操作,依然维护单调性⭐
-
- 问题性质:最近(大于/小于)关系
- 入栈之前,符合单调性的栈顶元素,就是当前入栈元素的最近(大于/小于)关系
- 维护的核心:栈顶元素——最近(大于/小于)关系⭐
- 左侧最近关系→左侧先入栈
- 右侧最近关系→右侧先入栈
- [PS] 其栈底是全局最小值,但用栈维护并没有意义
- 均摊时间复杂度:O(1),求解一次
两者对比
其实两者主要是形式上不同,但本质差不多
| |开放端口|维护核心|擅长问题|基本操作|
|:----😐:----|:----😐:----|:----😐:----|:----😐:----|:----|
|单调队列|首、尾|队首|区间最值|维单+入队、出队、取值|
|单调栈|顶|栈顶|最近大小关系|出栈[维单]、取值、入栈|
随堂练习
——引入——
HZOJ-261:数据结构

样例输入
8
I 2
I -1
I 1
Q 3
L
D
R
Q 2
样例输出
2
3
- 思路
- 数据规模:
-
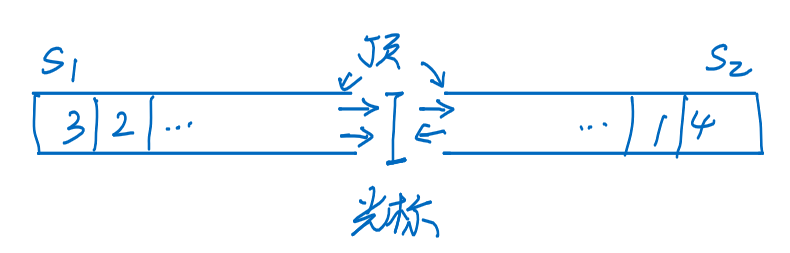
- 【关键】类比终端的光标操作,维护光标所在的位置⭐
- 【数据结构】对顶栈,两个栈s1、s2的栈顶对应光标位置 [也可用数组或链表模拟]
- 【操作分析】
- 插入:s1入栈某元素
- 删除:s1出栈
- 左移:s1栈顶元素转移到s2
- 右移:s2栈顶元素转移到s1
- 查询:维护一个前缀和数组sum以及最大前缀和数组ans,ans中存的就是答案
- [PS] 如果用单纯一个数组实现,插入很耗时
- 代码
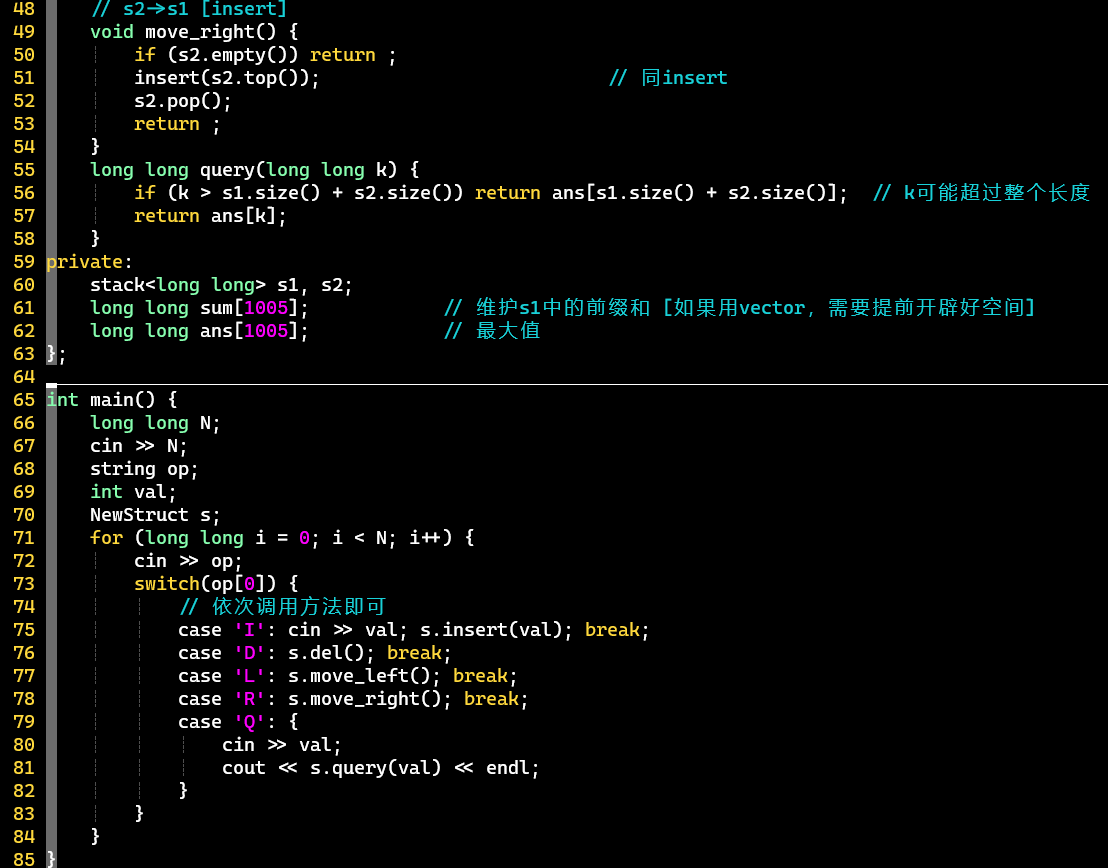
- 新造一个数据结构 -> 结构定义 + 结构操作
- 定义好数据结构后,可以很方便地使用其方法
- 维护前缀数组sum和与最大前缀和数组ans的时机
- 在向s1插入元素时:插入操作、右移操作
- 删除操作、左移操作本也需维护,但HZOJ的测试样例存在BUG:查询时的k值,在大于光标当前位置 [即s1.size()] 时,答案仍考虑1~k的最大前缀和,所以需要保留s2中每个位置对应的最大前缀和
- [PS]
- sum、ans数组第0位需要保留一个初始值,用于初始的前缀和累加和比较
- ans的数据只负责比较,不负责运算;sum的数据只负责运算,不负责比较
- 查询操作输入的k可能比总长度大,所以也可以特判一下,返回整体的最大前缀和
HZOJ-263:火车进栈
样例输入
3
样例输出
123
132
213
231
321
- 思路
- 注意题干:1~n 按顺序进站;输出前20种答案
- 首先思考样例输出中,会有312吗?
- 如果想要第一个得到3,需要压入1、2,那么出栈只能是321
- 【关键】判断全排列中的序列是否合法
- 假设,已经进栈的最大列车编号,为;全排列的一个序列中当前待出栈的的数字是
- 如果,说明必须是栈顶元素,否则序列不合法
- 如果,先将中的所有元素入栈,此时栈顶元素一定是y
- 举例:判断4132、3241是否合法?
-
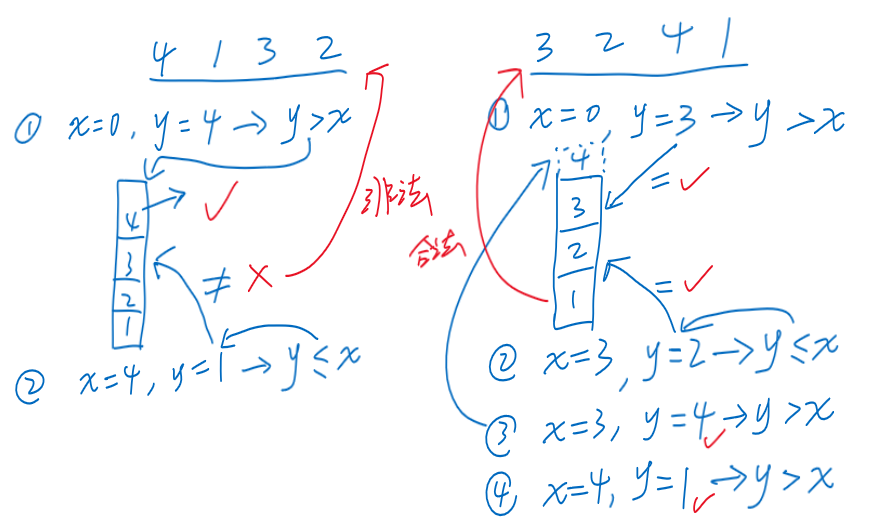
- 注意、的比较,只会增或者不变,不会减
- 可自行模拟一遍
-
- 代码
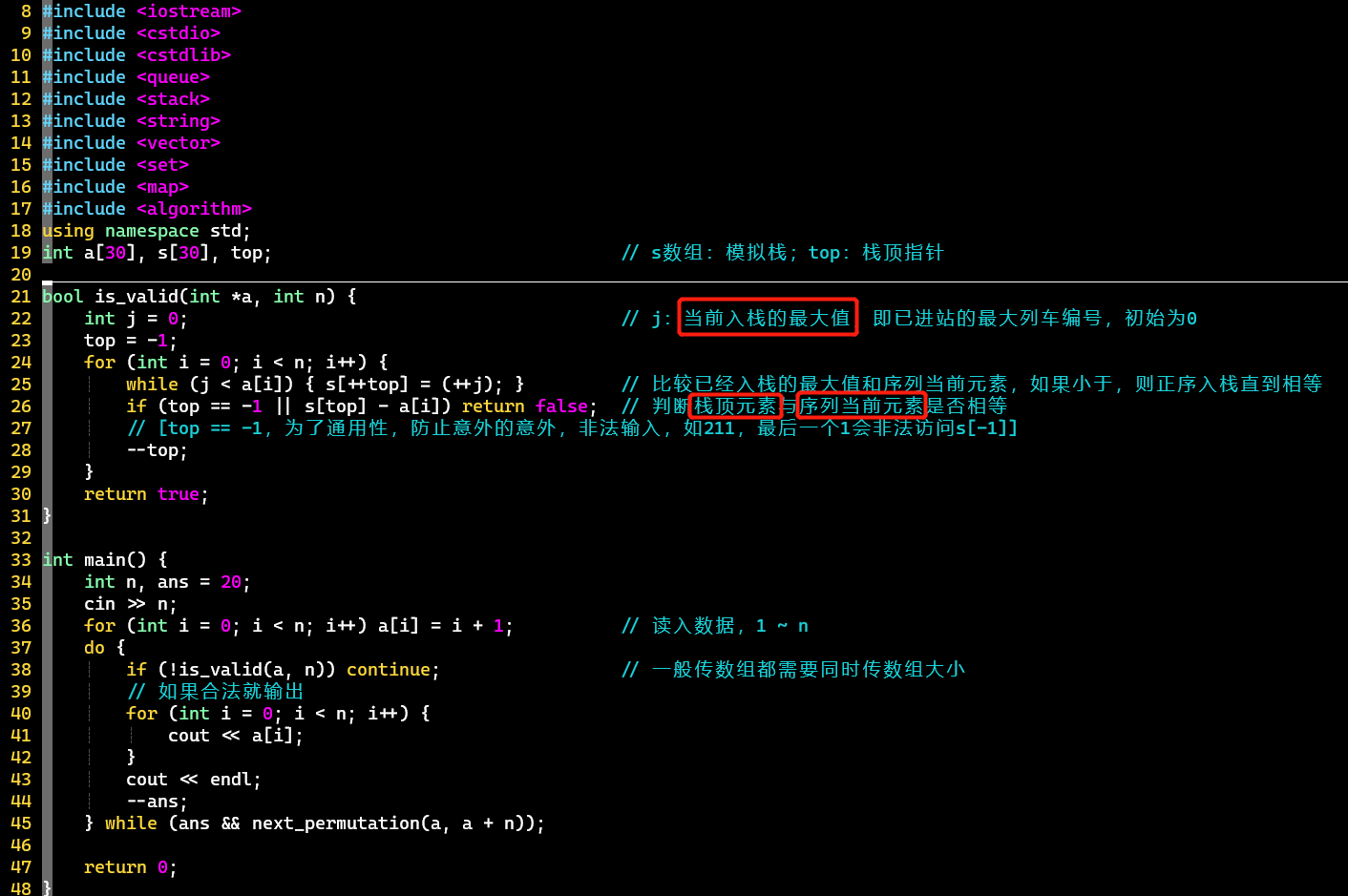
- 注意栈中栈顶指针和当前入栈的最大值的巧妙利用 [栈用数组模拟]
- top == -1的判断是为了通用性,在这里不会存在
- 利用函数
bool next_permutation(begin, end)得到下一组排列 [按字典序升序的],返回值代表是否有下一组排列
——单调队列——
HZOJ-271:滑动窗口
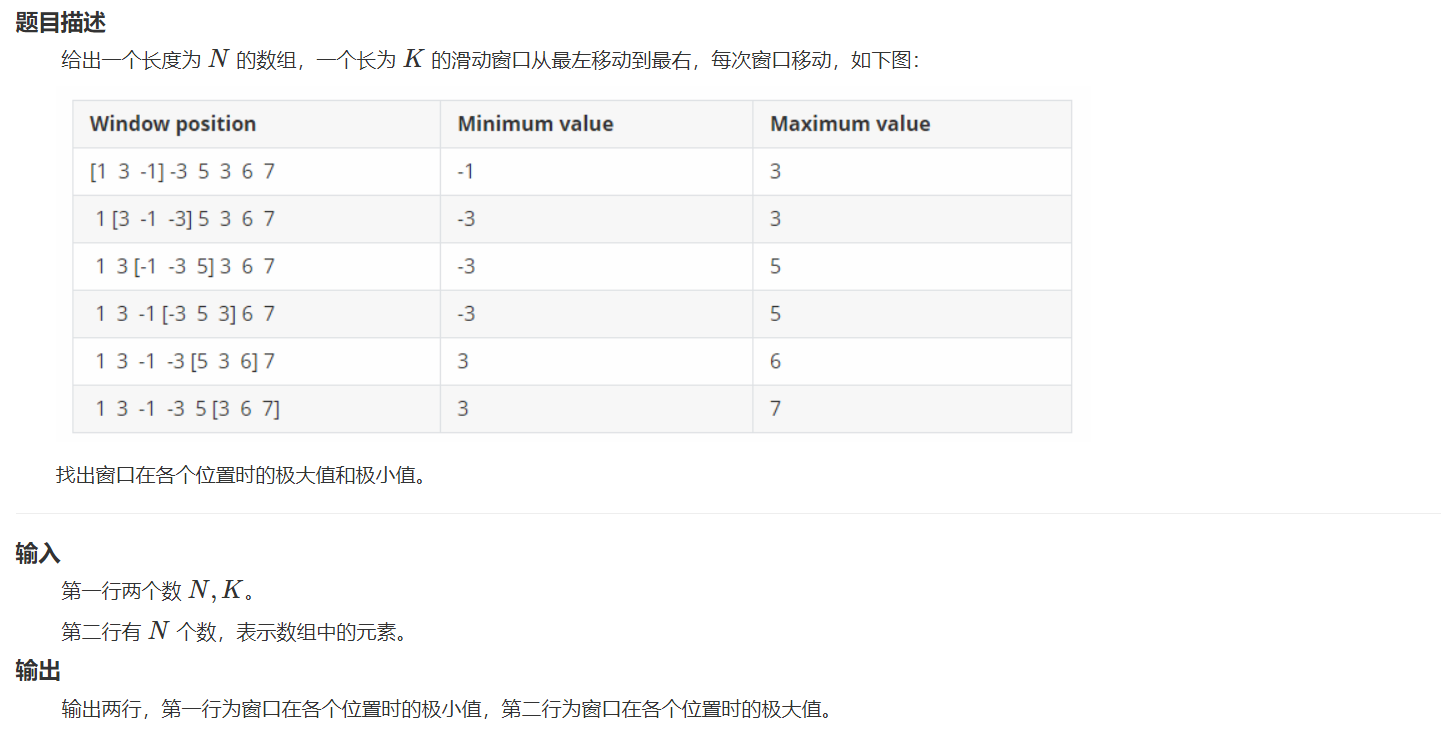
样例输入
8 3
1 3 -1 -3 5 3 6 7
样例输出
-1 -3 -3 -3 3 3
3 3 5 5 6 7
- 思路
- 数据规模:
- 纯单调队列,关注代码实现
- 代码
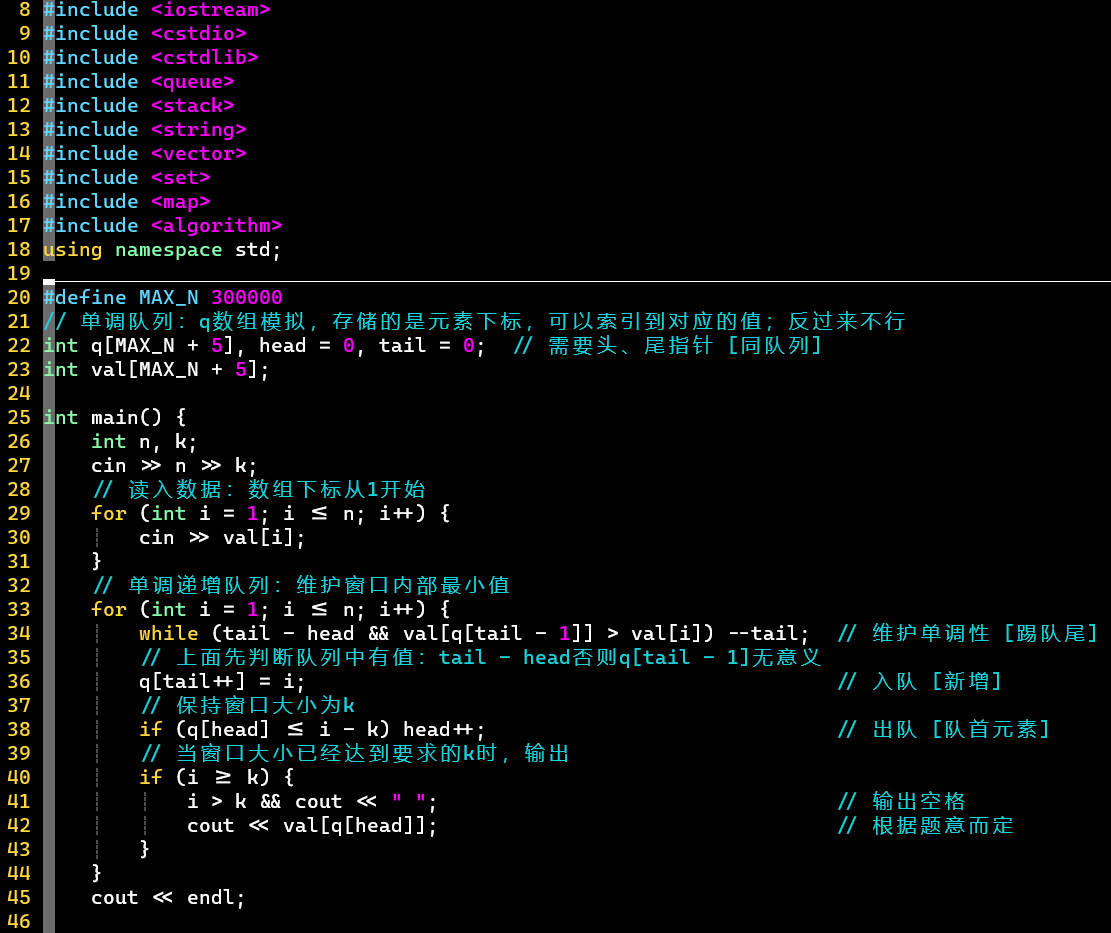
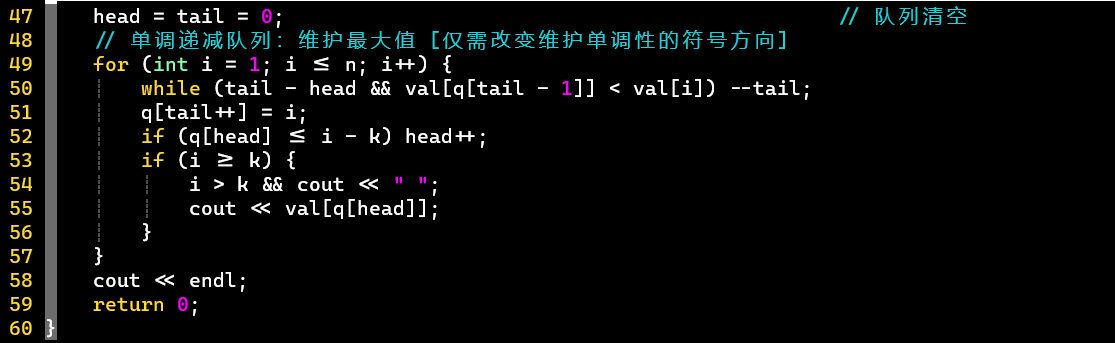
- 思考:单调队列中是记录值还是记录【下标】
- 记录下标🆒,因为有了下标可以索引到值 [顺藤摸瓜]
- 记录值,却反向不可查
- 这是一个常用的单调队列模板:维护单调性→入队→出队→根据题意输出
- 关注最大/小值、窗口的大小
- [PS] 队尾既可以入队,也可以出 [踢,维护单调性],所以认为不是单向队列
HZOJ-372:双生序列

样例输入
5
3 1 5 2 4
5 2 4 3 1
样例输出
4
- 思路
- 思考:什么是两个序列的趋势相同?
- 相同区间内部的RMQ值相同,❗ 这里RMQ值→最小值的最大下标
- 【关键】两个序列的每个区间的RMQ值相等👉两个序列的单调队列长得一样
- 换句话说,每时每刻,两个序列对应相同的单调队列
- 注意:长得一样,指的不是最小值,而是对应下标 [单调队列里存的是下标]
- 将两个序列的元素,依次插入到单调队列中,每次插入后比较单调队列的大小即可
- ① 如果一致,继续入队
- ② 如果不一致,输出答案
- 思考:什么是两个序列的趋势相同?
- 代码
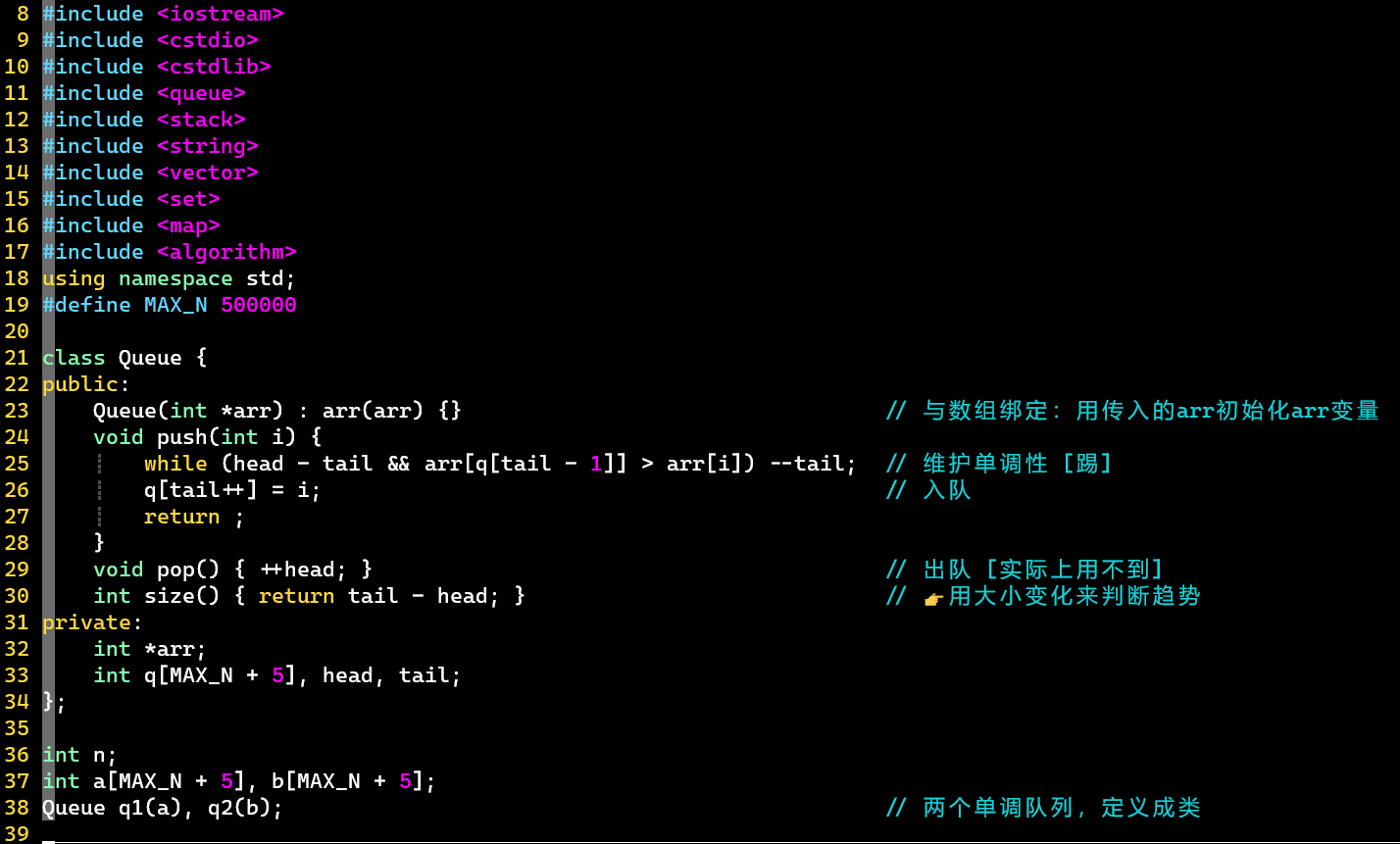
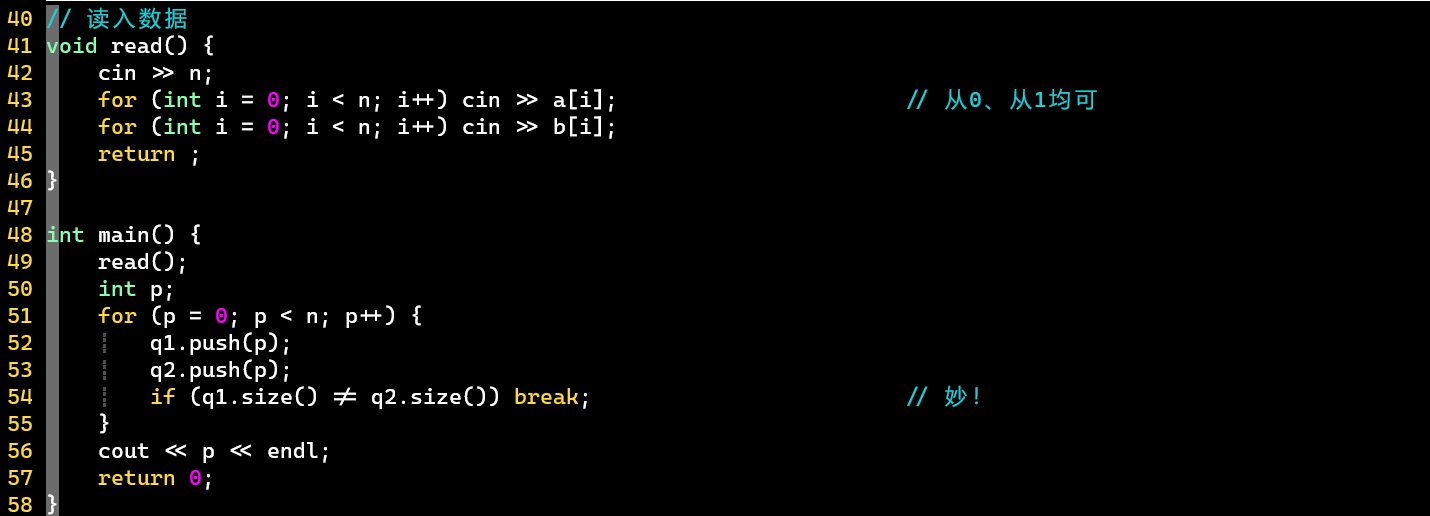
- 用类定义单调队列,便于复用
- 单调队列里存的是下标:p
- 单调队列操作:维护→入队,都不需要出队
- 【巧妙】根据队列的大小变化把握趋势变化
HZOJ-270:最大子序和

样例输入
6 4
1 -3 5 1 -2 3
样例输出
7
- 思路
- 子序和 → 区间和,利用前缀和可得
- 限定条件:子序列的长度不超过→ 滑动窗口
- 因此,转换为前缀和数组上的问题
-
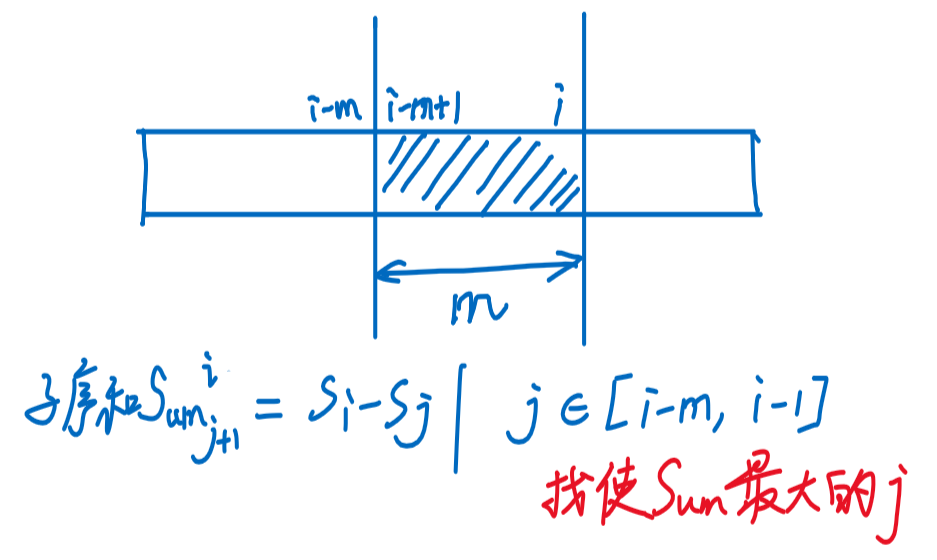
- 目标:,即找最小的,得到
- 代表原序列前个元素的和
-
- 【问题转换】
- 在前缀和数组上,维护一个大小为的滑动窗口的最小值
- 👉 单调队列。注意:维护的不是原序列,而是前缀和数组
- 代码
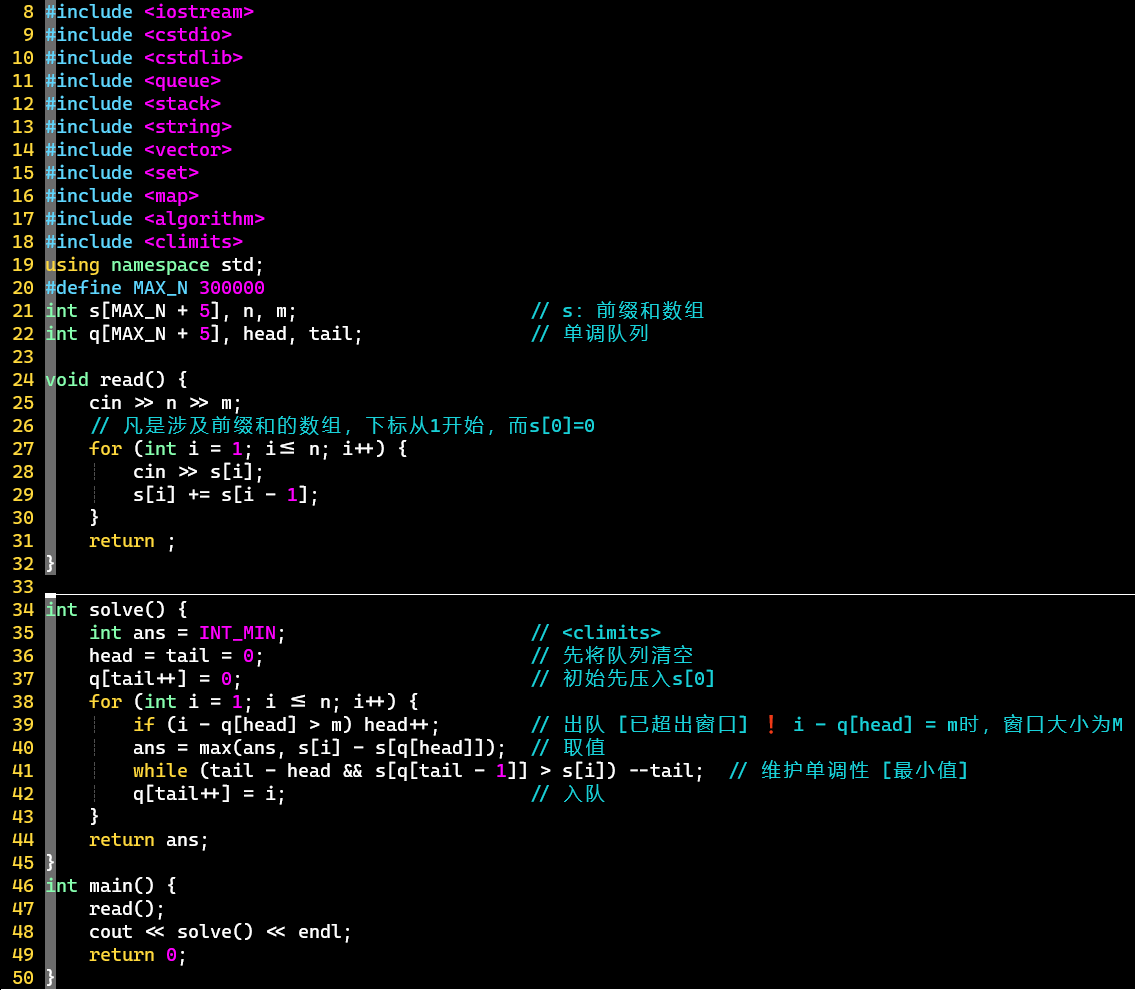
- 单调队列操作:出队→取值→维护单调性 + 入队
- 本来套路是先维护单调性 + 入队,即,出队和取值操作放在后面 [这样是没问题的]
- 但调换了顺序也可以:因为窗口大小,所以队列中至少最后一个元素用不到,所以取值放在前面也不会漏值
- [PS] 出队操作只要在取值前即可
- 只需要前缀和信息,原信息不用建立数组
- ❗ 对于求区间和,不要忘记前缀和数组0号元素的意义,单调队列初始记得压入它
——单调栈——
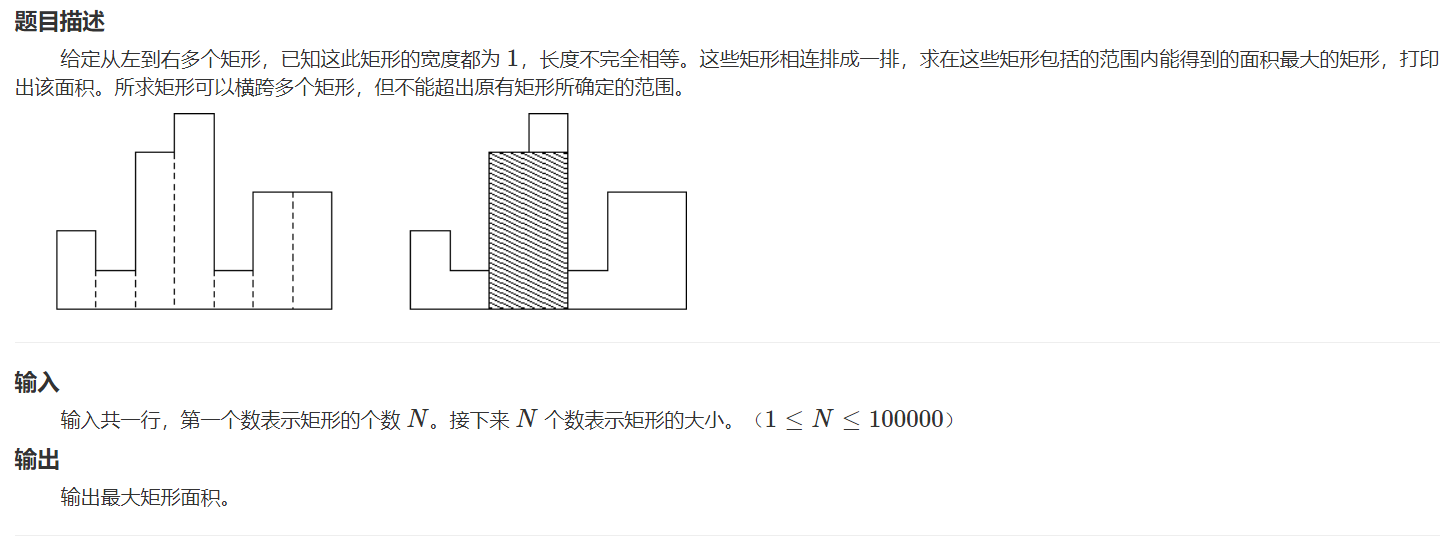
HZOJ-264:最大矩形面积
样例输入
7
2 1 4 5 1 3 3
样例输出
8
- 思路
- 思考:最大矩形的性质 ——> 矩形高度 = 所在区域最矮的木板高度 x
- 如果矩形高度 > x,不能构成矩形
- 如果矩形高度 < x,为什么不能 = x 呢?
- 具体思路
- 反过来,确定以某一块木板作为当前矩形的高度,向左向右找第一个比它小的高度,中间的面积就是其能得到的最大矩形面积
- 再遍历每一块木板求得的最大面积,取最大值
- 需要求解:每一块木板最近的高度小于当前木板的位置,所以使用【单调栈】
- [启发] 分析最优解的性质,是解决问题的第一步
- 思考:最大矩形的性质 ——> 矩形高度 = 所在区域最矮的木板高度 x
- 代码

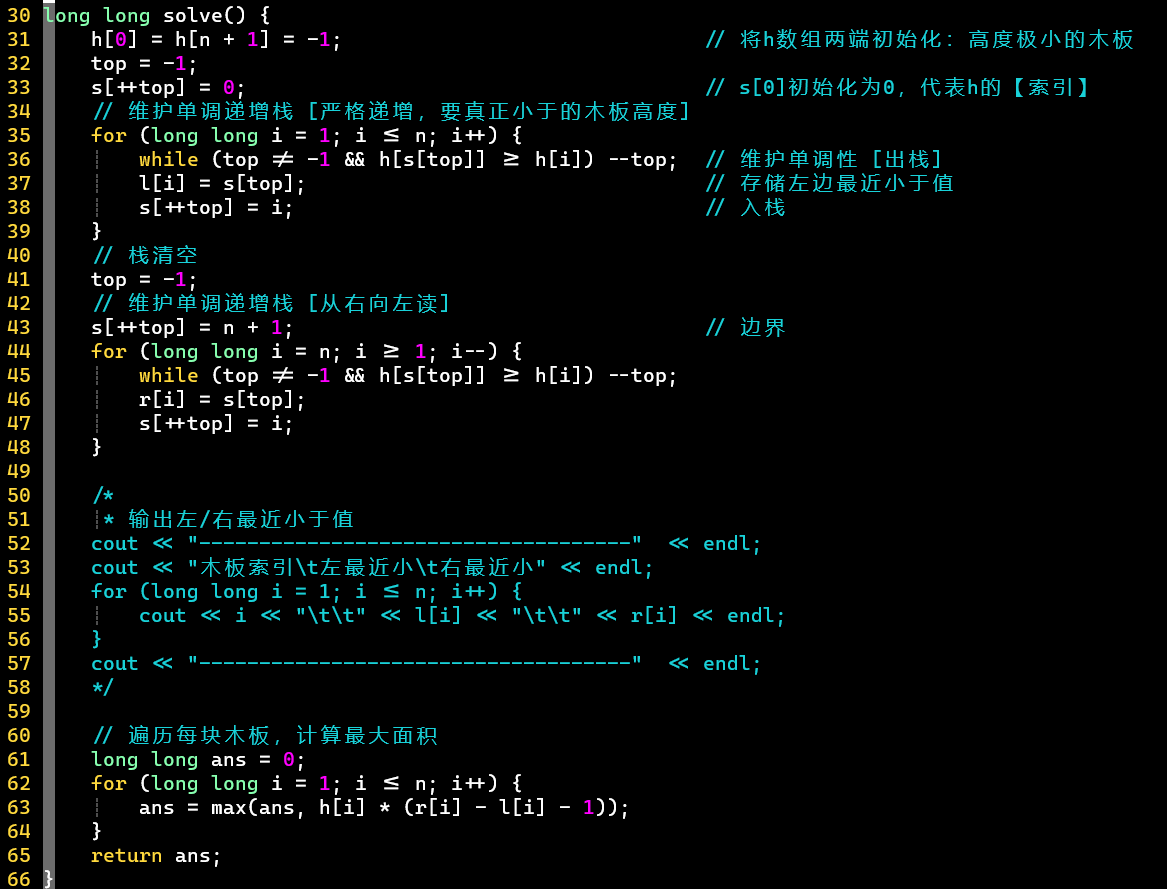

- 需要数组存储的数据有:木板高度数据、单调递增栈、存储左 / 右最近最小
- 要注意边界的处理技巧:两端设置高度极小的木板 [-1],同时初始化好栈底,为高度极小的木板的索引 [0、n + 1]
- 最后将左/右整合到一起,计算面积,取最大即可
- 这也是一个常用的单调栈模板:维护单调性 [出栈] →根据题意取值→入栈
- 样例解析:
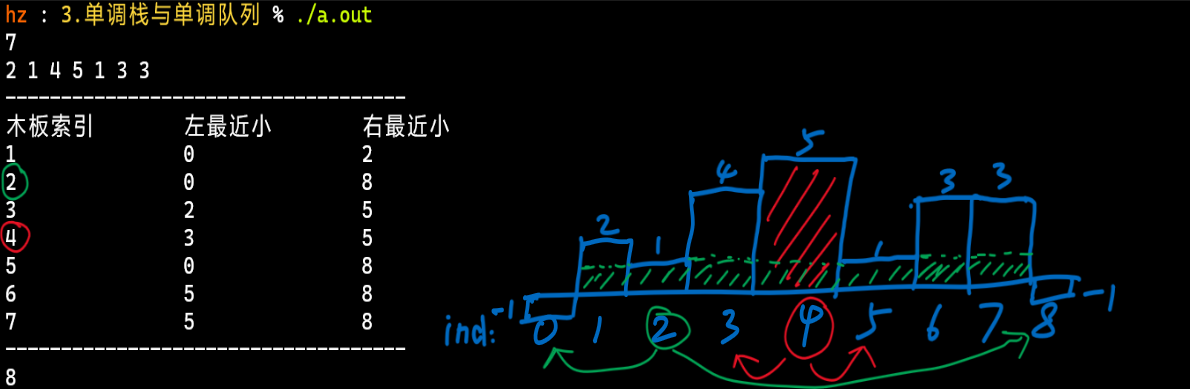
- 注意单调栈里存储的是索引值
Tips
- 结合单调队列/栈的动态规划问题请跳转:2 从递推到动态规划(下)