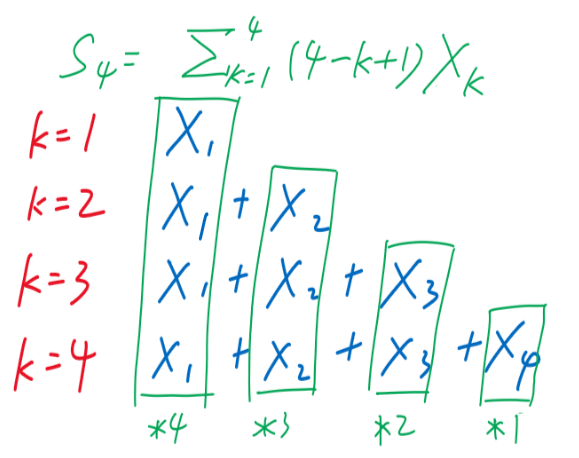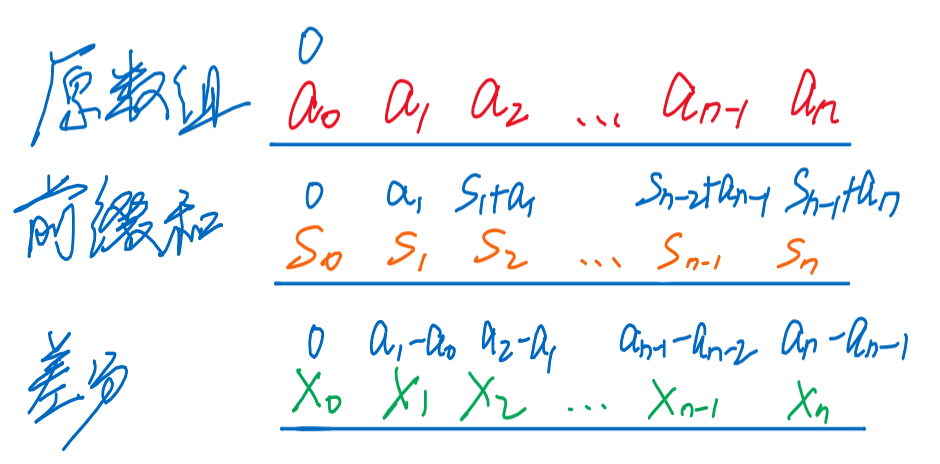课程内容

前缀和数组与差分数组

【假设】原数组$a$：$a_i,\ i\in[0,\ n]$，注意$a_0=0$[否则差分数组的前缀和不等于原数组]

【可得】

• 前缀和数组$S$：$S_i = \sum_{k=0}^{i}{a_i}$，易得$a_i = S_i - S_{i-1}$[差分]
• 差分数组$X$：$X_i=a_i-a_{i-1}$，易得$a_i=\sum_{k=0}^{i}X_i$[前缀和]

【观察】

• 前缀和数组、差分数组，并没有增加信息，只是信息的另一种表现形式
• 已知一个数组，就可以推出其他数组
  • 已知$a$数组：——前缀和——>$S$数组、——差分——>$X$数组
  • 已知$S$数组：——差分——>$a$数组
  • 已知$X$数组：——前缀和——>$a$数组
• [PS] 前缀和操作和差分操作，实际上是两个互逆的操作
• ❗ 但是不同的表现形式，对不同的操作，将对应不同的时间复杂度，见下

【问题引入】

① 原数组区间和操作

• $a$数组上操作：$O(n)$
• $S$数组上操作：$O(1)$，由$S_i-S_{j-1}$可得$a$数组$[j,\ i]$区间和

② 原数组区间修改操作

• 修改前：
  • $a$数组上：$a_0,a_1,a_2,a_3,a_4,a_5,a_6$
  • $X$数组上：$X_1=a_1-a_0,X_2=a_2-a_1,X_3=a_3-a_2,X_4=a_4-a_3,X_5=a_5-a_4,X_6=a_6-a_5$
• 修改后：[区间加]
  • $a$数组上：$a_0,a_1,a_2[+d],a_3[+d],a_4[+d],a_5[+d],a_6$
  • $X$数组上：$X_1=a_1-a_0,X_2=a_2-a_1[+d],X_3=a_3-a_2,X_4=a_4-a_3,X_5=a_5-a_4,X_6=a_6-a_5[-d]$
• 可见
  • $a$数组上操作：$O(n)$
  • $X$数组上操作：$O(1)$

【结论】

• 前缀和数组：优化区间和操作
• 差分数组：优化区间元素修改操作

【思考】❗

• 前缀和数组的单点修改效率是$O(n)$，因为需要修改变化点及之后的所有前缀和元素值
• 前缀和数组元素值与之前原数组中所有项都有关系！那么，如何弱化这种关系呢？

👉树状数组：弱化上面这种关系，损失一点查询效率 [取舍]

lowbit函数

【树状数组中的关键】

• $lowbit(i)$：代表$i$这个数字，二进制表示的最后一位1的位权
• 计算公式：$lowbit(i) = i\ \&\ (-i) = i\ \&\ (\sim i + 1)$
• 举例：$lowbit(10010000)$
  • 
  • 得到了最右的1的位置，很巧妙
• 负数用补码表示法：[负数的]补码 = [正数的]反码 + 1
  • 例如：$-3 = ~3 + 1 = ~0011 + 1 = 1101$
  • ❗ 补码表示法将减法变成了加法 [计算机中没有减法]

树状数组

⭐树状数组本质上是对前缀和数组的一种优化，主要体现在单点修改操作上

直观对比：前缀和数组

• 
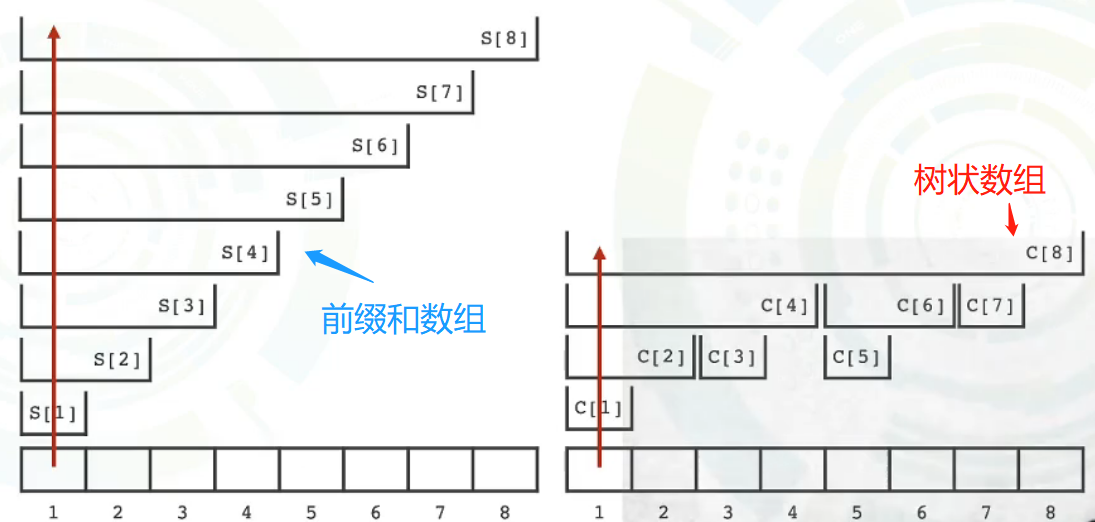
• 树状数组中，$C[i]$代表从$a[i]$开始的前$lowbit(i)$项的和
• 树状数组更加扁平化
• 两者空间消耗相同

前缀和查询

• 
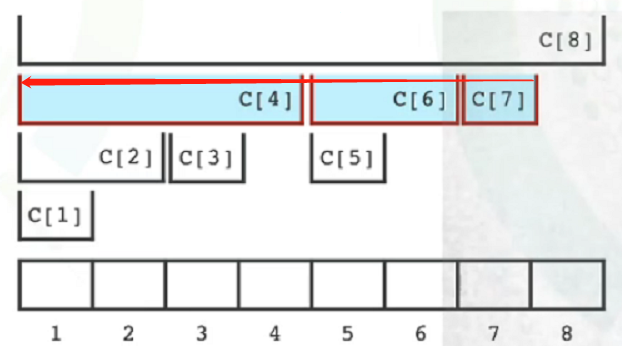
• 前缀和：$S[i]=S[i-lowbit(i)]+C[i]$
• 例如
  • $S[7]=S[7-1]+C[7]=S[6-2]+C[6]+C[7]=C[4]+C[6]+C[7]$
  • $S[12]=S[12-4]+C[12]=C[8]+C[12]$
• 时间复杂度：$O(log\ n)$
• [PS]$(i)_2$中1的个数，即前缀和的组成元素数量

单点修改

• 
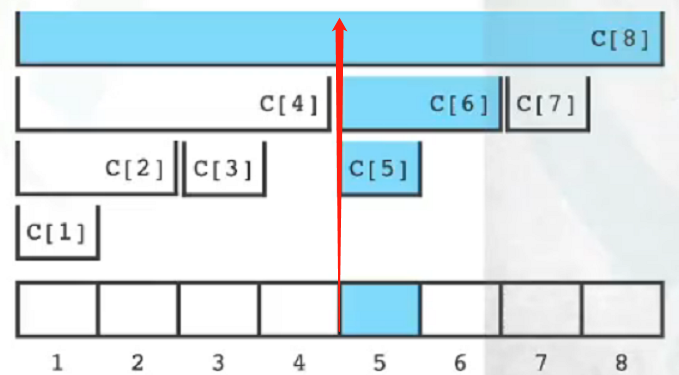
• 修改位置$i$的值，需要不断修改$f(i)=i + lowbit(i)$位：$C[i],\ C[f(i)],\ C[f(f(i))],\ ...,\ until\ index\gt n$
• 例如
  • 修改$a[1]$：$C[1],C[2],C[4],C[8]$ <而对于普通的前缀和数组，需要修改前8项>
• 时间复杂度：$O(log\ n)$

小结

• $lowbit()$函数：至关重要
• 两种操作
  • 前缀和查询：向前统计，每次查$i$的前一位——> $i - lowbit(i)$，直到$i=0$
  • 单点的修改：向后修改，每次修$i$的后一位——> $i + lowbit(i)$，直到$i>n$
• 时间效率
  • 前缀和查询：$O(log\ n)$，单点修改：$O(log\ n)$
  • 相比最普通的前缀和数组：查询变差，单点修改变优，综合时间复杂度变优
• 使用前提：必须可以转化成前缀和问题

随堂练习

HZOJ-329：弱化的整数问题

样例输入

5
1 5 3 2 4
2
C 1 5 1
Q 3

样例输出

4

• 思路
  • 涉及区间修改、单点查询操作
    • 区间修改👉差分数组的单点操作 ① [最优，详见上文]
    • 单点查询👉差分数组的前缀和 ②
  • 既要维护前缀和 ②，又要进行单点修改 ①，所以
    • ⭐可以使用树状数组，维护原数组的差分数组
    • 当然也可以使用线段树
• 代码
  • 
  • 
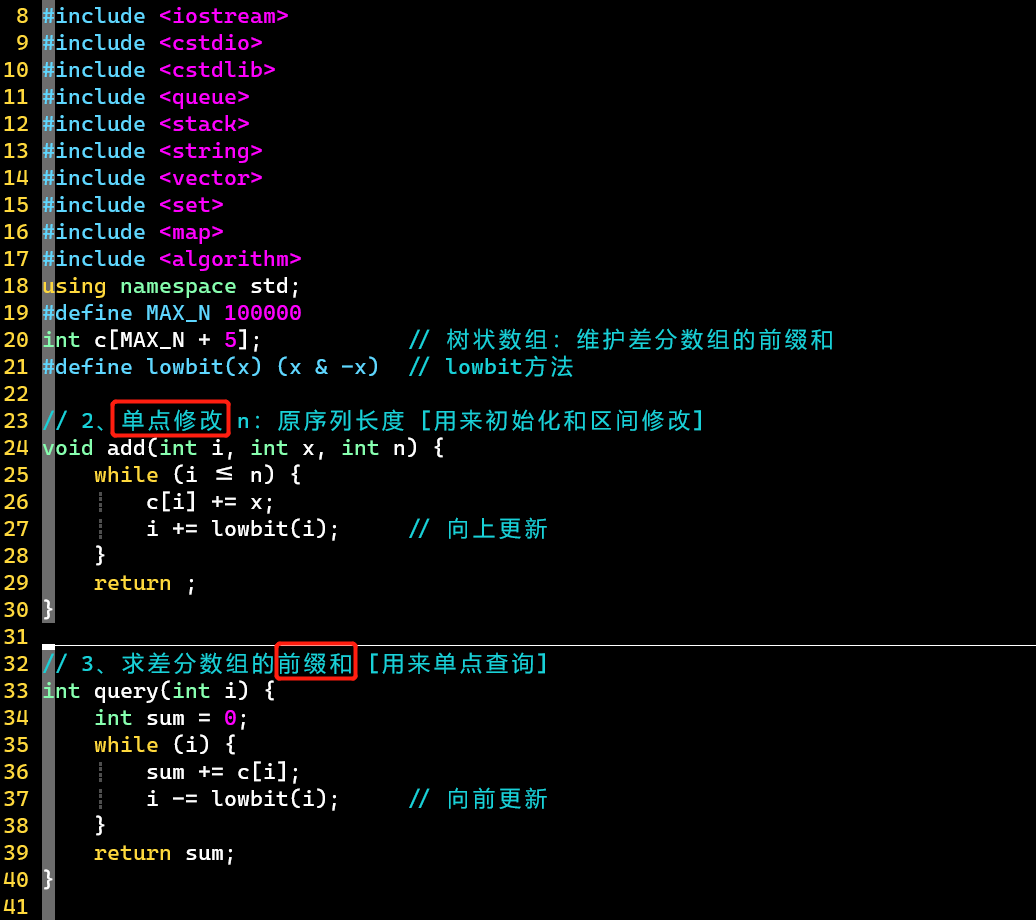
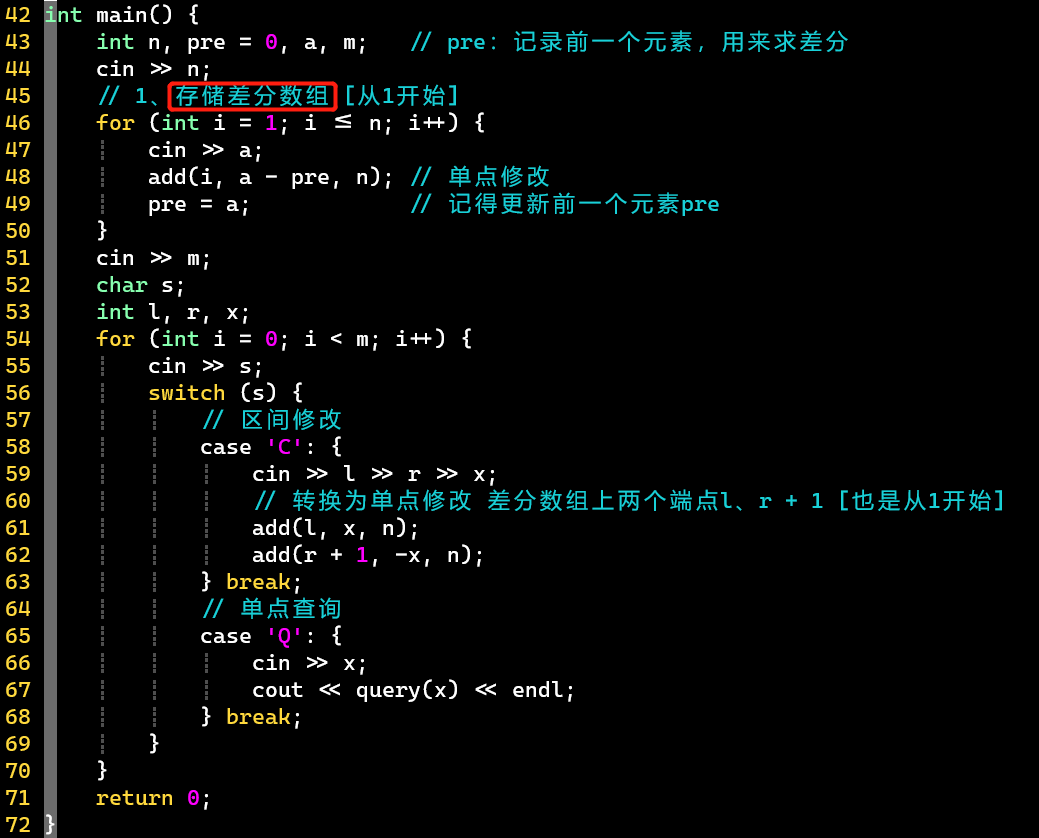
  • ❗ 将区间修改操作放在差分数组上，转换为【单点修改】；将单点查询操作，转换为差分数组的求【前缀和】
  • 学习树状数组的代码，其实现一般都不会变 [通用性很强]
    • ⭐ 单点修改、求前缀和
  • 存储差分数组，使用一个pre变量记录前一个元素
  • [PS] 差分数组和前缀和数组的下标一般都是从1开始，因为它们的第0位均为0

HZOJ-330：加强的整数问题

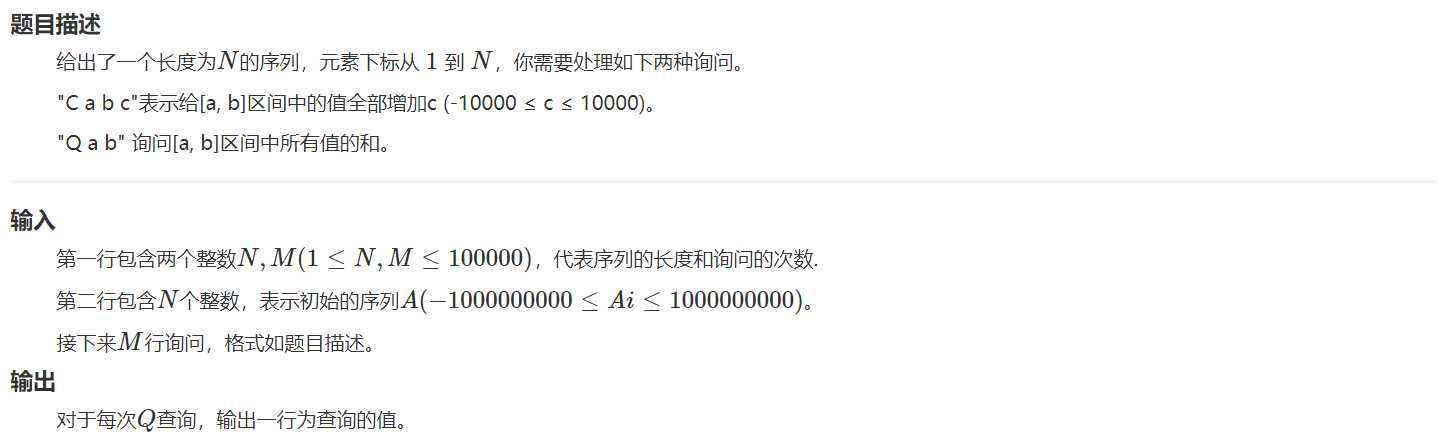
样例输入

5 2
1 5 3 2 4
C 1 5 1
Q 1 5

样例输出

20

• 思路
  • 涉及区间修改、区间查询操作
    • 区间修改👉差分数组的单点修改 ① [同上一题：OJ-329]
    • 但如何区间查询呢？👉两个前缀和 ②，见下
  • 区间查询问题转换
    • ① 因为引入差分数组，所以要围绕差分数组来对区间和问题做转换
    • ② 区间和$Query(l,r)=S(r)-S(l-1)$，所以重点分析$S$转换到$X$[差分数组]
    • ③ 推导如下等式
      • $\begin{aligned}&S_i=\sum_{k=1}^ia_k=\sum_{k=1}^{i}\sum_{y=1}^{k}{X_y}\\&=\sum_{k=1}^i[(i+1)X_k-k\times X_k]=(i+1)\sum_{k=1}^iX_k-\sum_{k=1}^i(k\times X_k)\end{aligned}$
      • 第一行等式显而易见
      • 第二行等式的推导见下
        • 对于$\sum_{k=1}^{i}\sum_{y=1}^{k}{X_y}\ (Ⅰ)$，假设$i=4$，罗列$k$值
        • 
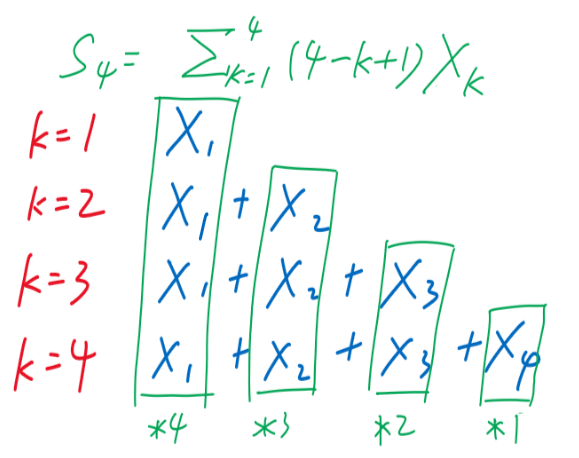
        • 通过观察可得，$(Ⅰ)=\sum_{k=1}^{i}[(i-k+1)\times X_k]$
        • 再将变量分组放置，即可
    • ④ 设$Y_k=k\times X_k$，则$S_i=(i+1)\sum_{k=1}^iX_k-\sum_{k=1}^iY_k$
    • 【结论】$S_i$可以通过2个与差分数组相关的前缀和数组得到，从而完成$Query(l,r)$问题
      • 需要维护两个树状数组
  • [PS] 维护的两个树状数组，都和差分数组相关，从而保证了区间修改时的时间效率
• 代码
  • 
  • 
  • 
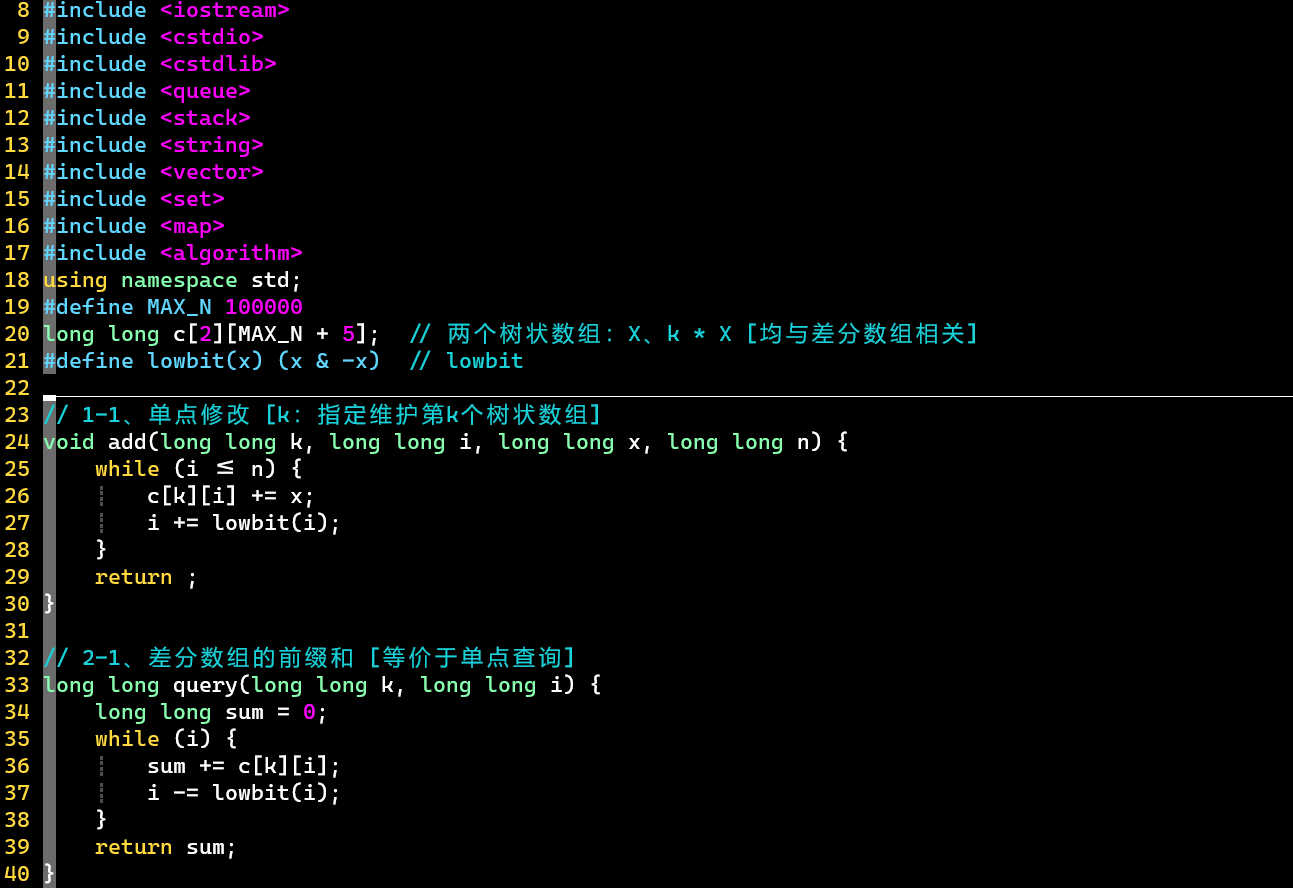
  • 关注整体思路，理清标号$0\to 2$
  • 主要方法
    • add、query方法：树状数组的基本操作，单点修改 && 求前缀和
    • modify方法：同时维护两个树状数组
    • S方法：通过2个差分数组的前缀和，求原序列的前缀和 [关注思路中推到的公式]
  • [思考] 维护的两个树状数组都与差分数组相关，所以在区间修改的时候，维护树状数组的时间复杂度还是$O(log\ n)$级别 [2 × 2次单点修改]
    • ❗ 如果想着区间查询，用原数组更方便，从而维护原数组和差分数组的树状数组。但是，在区间修改的时候，维护原数组的树状数组，时间复杂度是$O(n \times log\ n)$级别，还不如只用原数组，对应$O(n)$级别
  • [PS] 如果用char接收操作信息，scanf的时候需要考虑之前换行符的存在
    • 而cin不会有这个问题；用字符数组也不会有这个问题

附加知识点

• 树状数组 VS.线段树
  • 树状数组的代码更少
  • 空间上——$n：4n$[原数组大小为$n$]

Tips

• 可以联想前缀积版树状数组
  • 加法和乘法没有本质的区别，它们都是积性函数
  • [PS] 初始的0变为1，所有+=操作变为*=操作
• 树状数组的原理是什么？——知乎
  • 理解与$lowbit(i)$的关系