线段树知识请跳转:《面试笔试算法下》——4 线段树
树状数组知识请跳转:《面试笔试算法下》——5 树状数组
HZOJ-331:迷失的奶牛
Lost_cows

样例输入
5
1
2
1
0
样例输出
2
4
5
3
1
- 思路
- 【问题1】得到的答案是否唯一❓√
- 从后往前,反着来观察
- 最后一只小动物的值,是针对前面所有小动物的,也就是知道全部的信息了
- 所以,如果它的值是,即前面有个小动物比它小,则它的编号就是
- 进一步:对于倒数第二个小动物,它在除最后一个小动物的编号里,顺序找排名第的编号,即自己的编号
- 【问题2】怎么知道还剩哪些编号呢❓标记数组
- 用标记数组记录每一个编号 [下标] 是否可用,可用为1,不可用为0
- 此时标记数组中标为1的,即为可用的编号
- 用标记数组记录每一个编号 [下标] 是否可用,可用为1,不可用为0
- 大概过程如下图,按①→④的顺序
-
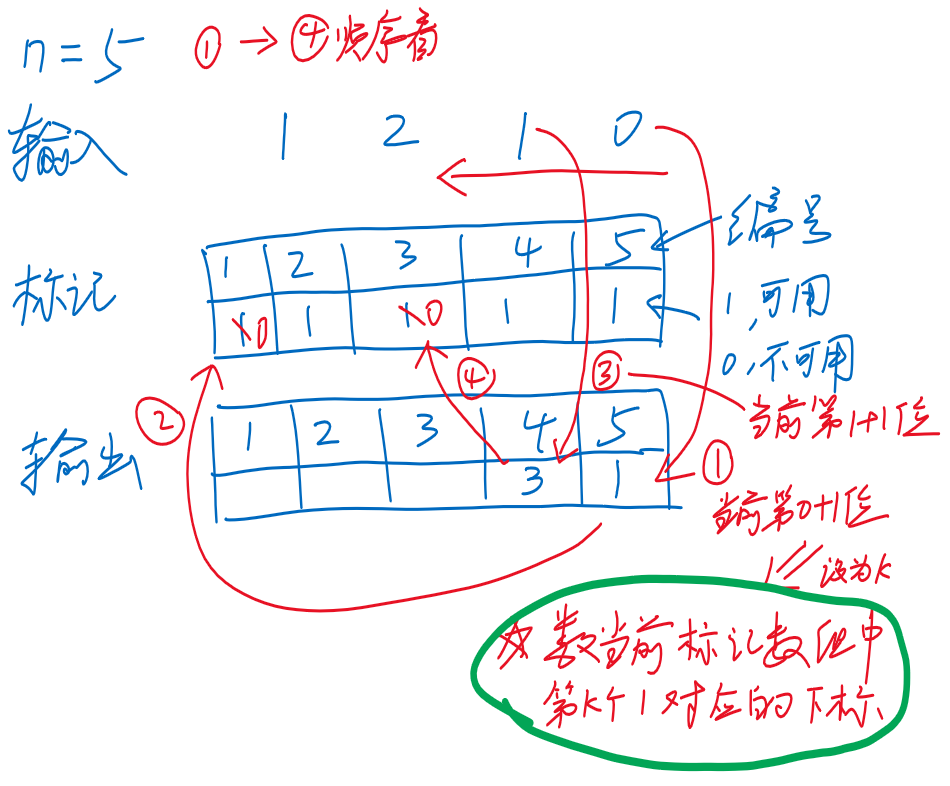
- 需要数当前标记数组中第个1对应的下标
- 例如,第③④步,当前奶牛比它前面的1个奶牛编号大,当前奶牛的编号就是当前剩余可用编号中的第2大编号,即3,再去标记
-
- 【问题转换】标记数组的前缀和
- 第个1对应的下标其实可以通过前缀和得到
- 标记数组上,第[编号] 位的前缀和,就代表第位前面可用编号的数量 [含自己],即[输入+1]
- 所以,在前缀和数组里,找首次出现的【】值,得到对应的【】下标
- 注意首次:即标记数组第位必须为1 [后面跟着的0不会增加前缀和]
- 【结论】⭐
- 从后往前观察,依次确定每一头奶牛的编号
- 在剩余可用的编号中找第【输入+1】位编号
- 维护标记数组的前缀和,该前缀和数组是单调的
- 所以可以在前缀和数组上,做二分查找,找首次出现的值,得到对应的下标
- 涉及到标记数组的前缀和维护与单点更新,所以可以使用树状数组
- 从后往前观察,依次确定每一头奶牛的编号
- 【关键技巧】标记数组,使用标记数组的前缀和
- 【PS】时间复杂度:
- 【问题1】得到的答案是否唯一❓√
- 代码
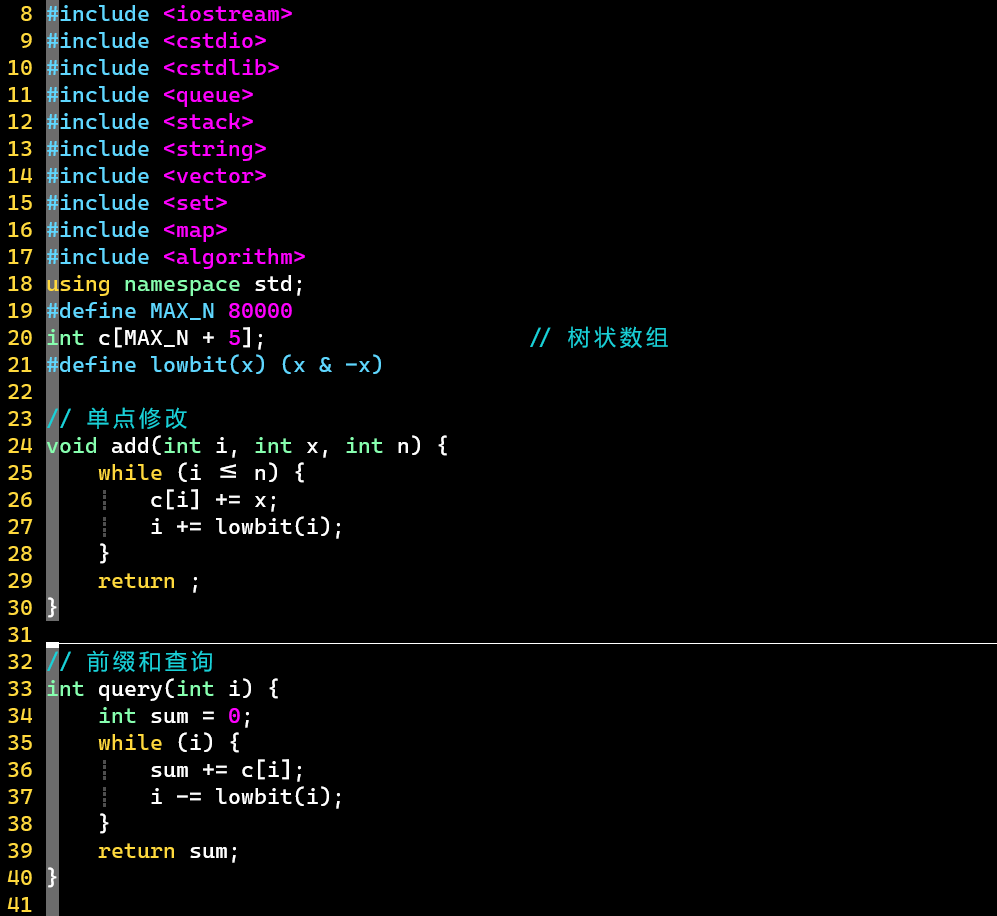
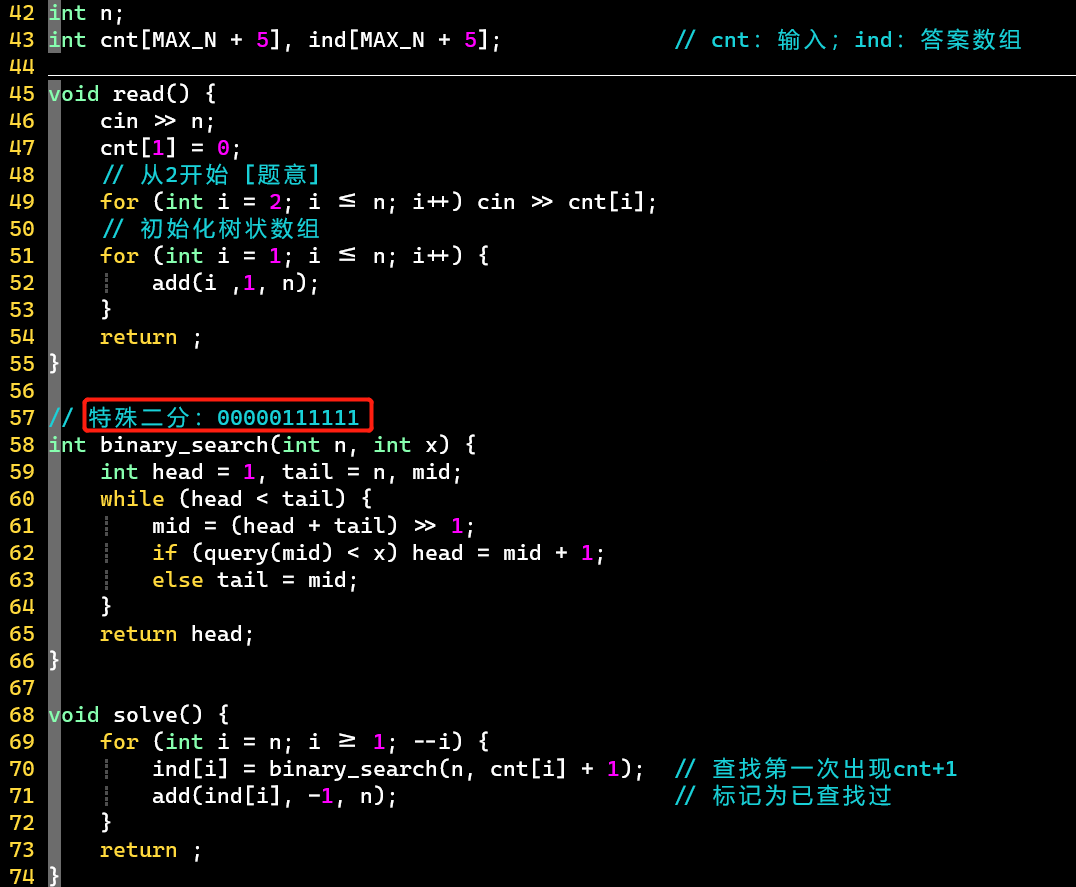

- 树状数组:维护标记数组,利用前缀和
- 查找的是首次出现的【输入+1】,对应第几位
- 注意首次!可能有多个对应【输入+1】值的下标,因为0的存在
- 找到后记得去标记,1->0
- [PS] 输入是从第2位开始的
HZOJ-332:买票

样例输入
4
0 77
1 51
1 33
2 69
样例输出
77 33 69 51
- 思路
- 与上题 [HZOJ-331] 相似
- 输入的第一列值 👉 代表在某个人前面有多少个人
- 同样倒着推,使用树状数组维护标记数组的前缀和,找第一次出现【输入+1】值的下标,再将下标[实际位置]与对应起来
- 与上题 [HZOJ-331] 相似
- 代码
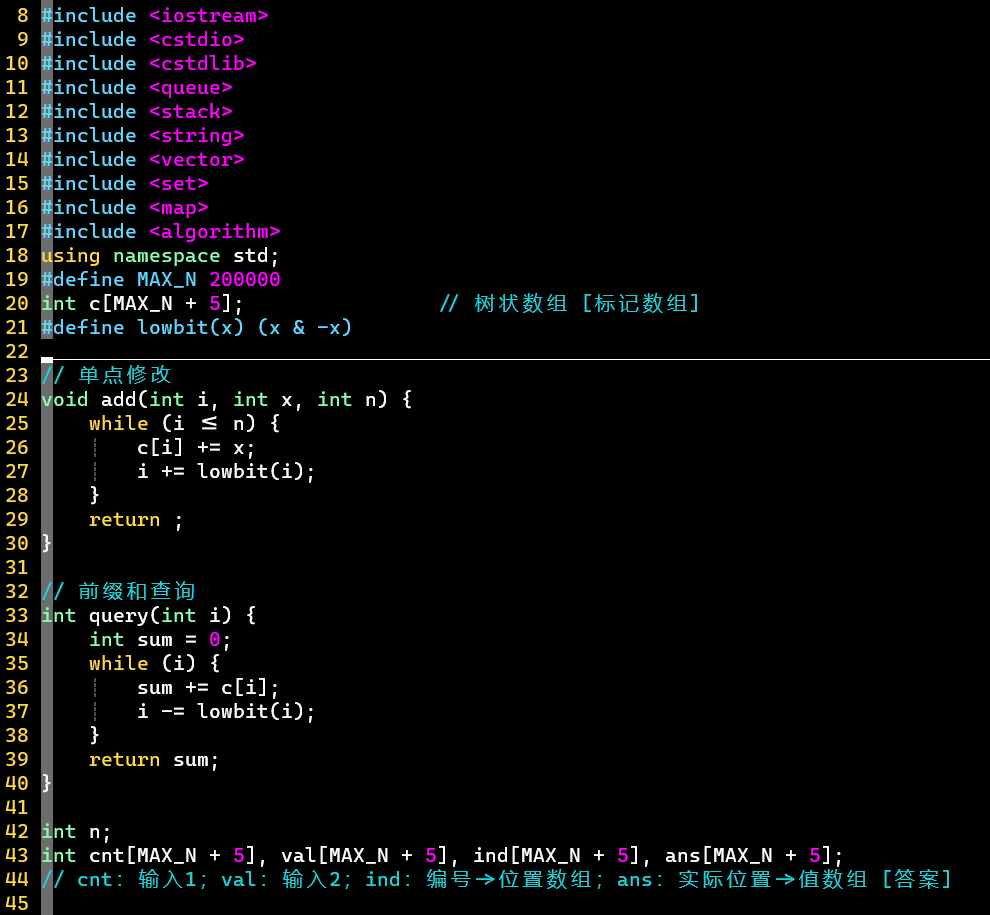
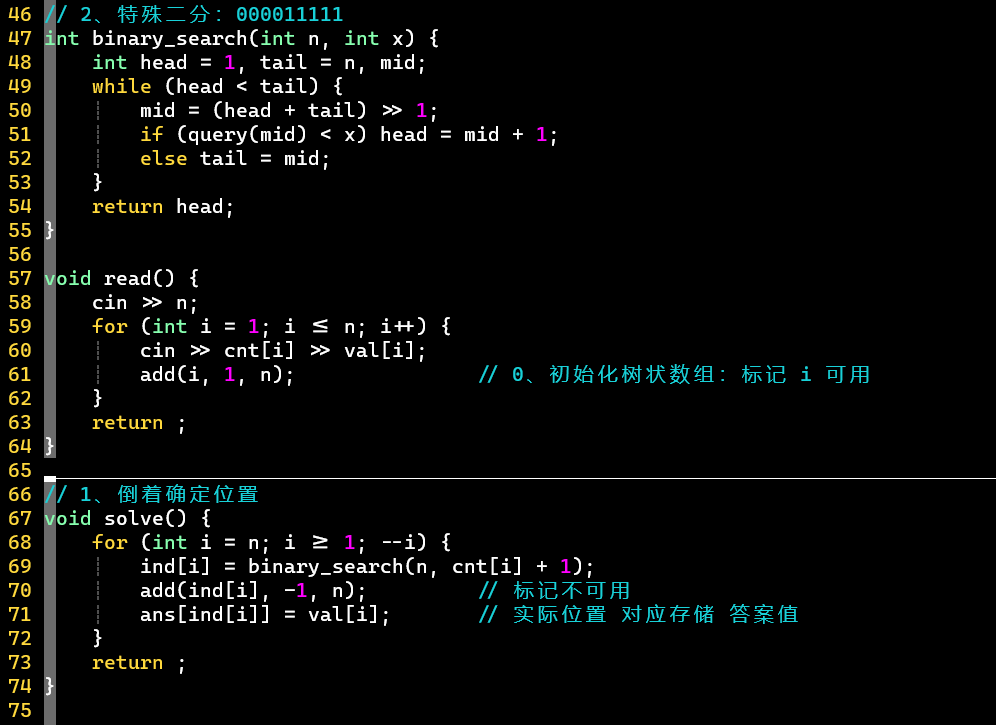

- 关键:倒着来👉特殊二分👉去标记 [维护树状数组]👉存答案数组
HZOJ-328:楼兰图腾

样例输入
5
1 5 3 2 4
样例输出
3 4
- 思路
- 【注意】输入是的一个排列
- 【关键】对于某一个点,经它组成的"^"的数量,为
- 其中,为前面值比它小的点数,为后面值比它小的点数
- 【问题】如何快速求解:前面小于该点的值的元素数量呢?
- 利用标记数组,记录当前位置之前有哪些元素出现过,出现过标记为1,否则标记为0
-
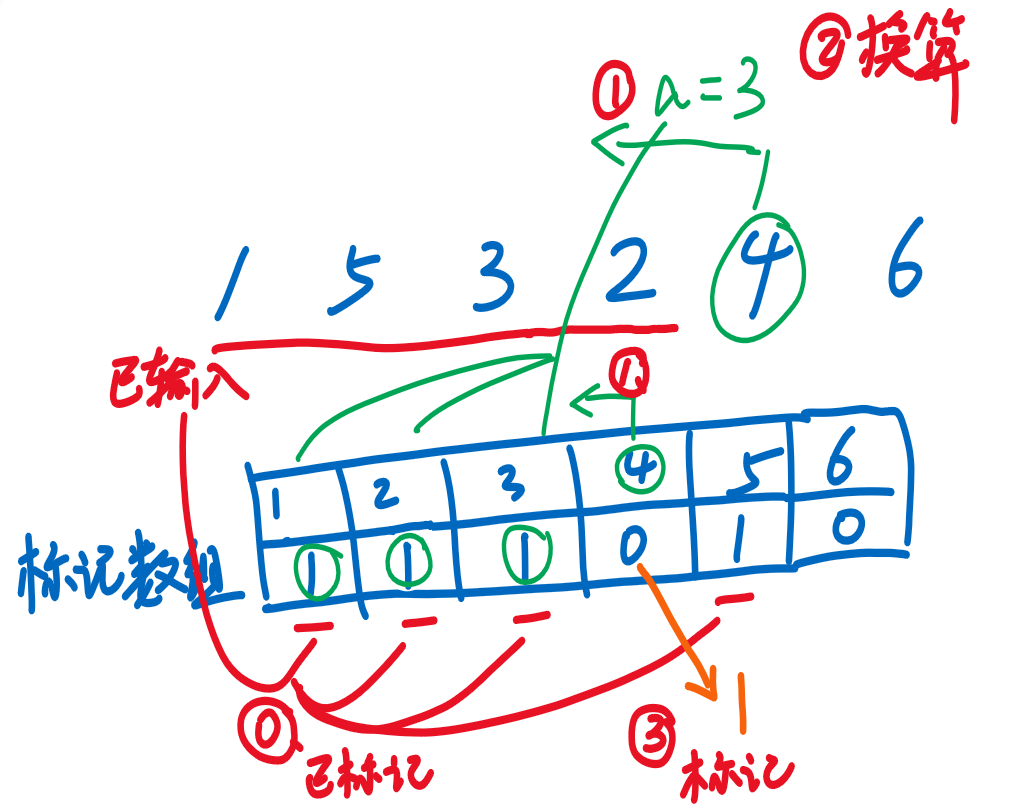
- 按照0️⃣→3️⃣的顺序捋:在到达值时,已经标记了值1、2、3、5,此时前面比X小的数量,换算得到,标记值4
- 【公式化】当前元素值记为,元素位置记为,则
- ① 前面小于X的元素数量是
- ② 后面小于X的元素数量是
- ③ 前面大于X的元素数量是
- ④ 后面大于X的元素数量是
- ⭐ 实际上
- 等于标记数组在位置之前的前缀和;后三个数量都可以通过换算得到
- ① × ② 得到"^"的数量,③ × ④ 得到"V"的数量
- 【数据结构】标记数组的单点修改及前缀和查询,可以使用树状数组
- 【PS】思想类似HZOJ-516:奶牛碑文——参考题解
- HZOJ-516可直接通过判等计算数量
- 而本题需要判断大小关系,所以使用了基于标记数组的树状数组
- 代码
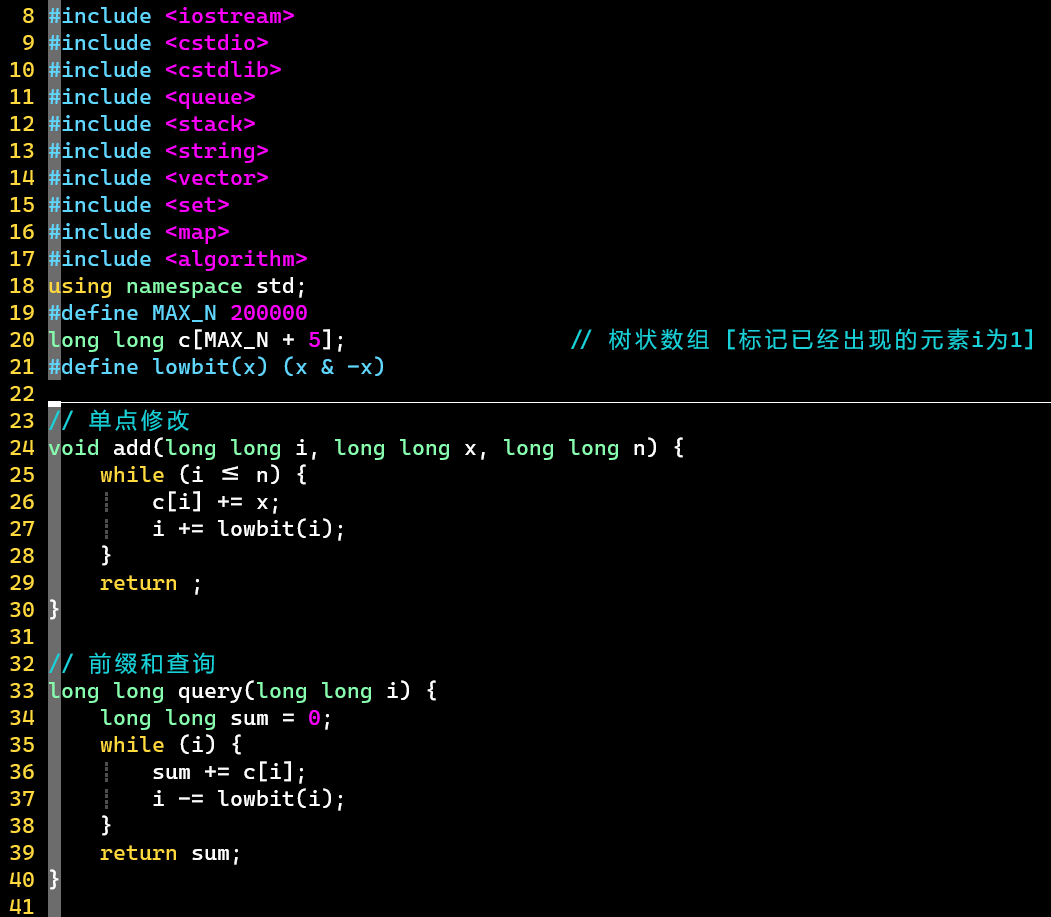
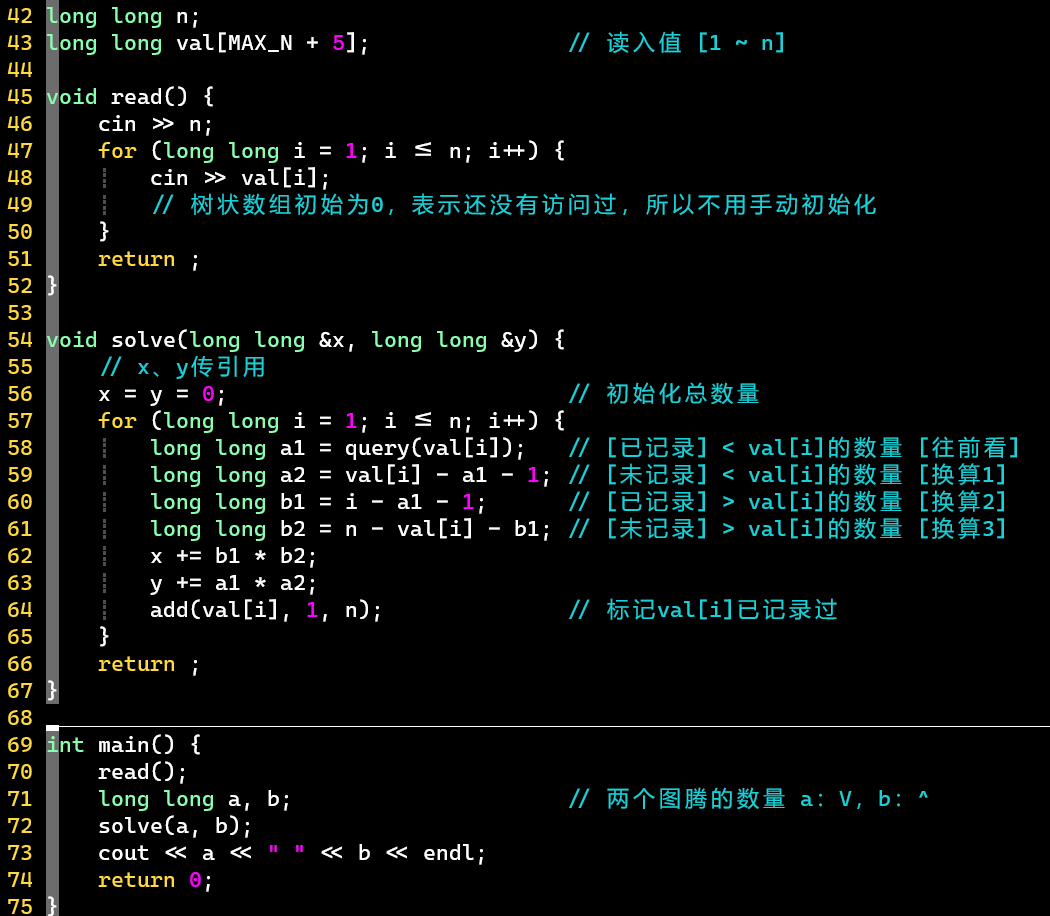
- 标记数组:出现过的元素标记为1
- 关注换算公式,可画图理解
- [PS] 将第64行修改为,再调换到第58行前,同样可行 [加深理解]
HZOJ-333:区间最大子段和

样例输入
5 3
1 2 -3 4 5
1 2 3
2 2 -1
1 3 2
样例输出
2
-1
- 思路
- 【关键】维护区间最大连续子段和;使用线段树
- 【思考】父结点所在区间的最大子段和,有3种可能来源,取最大即可
-
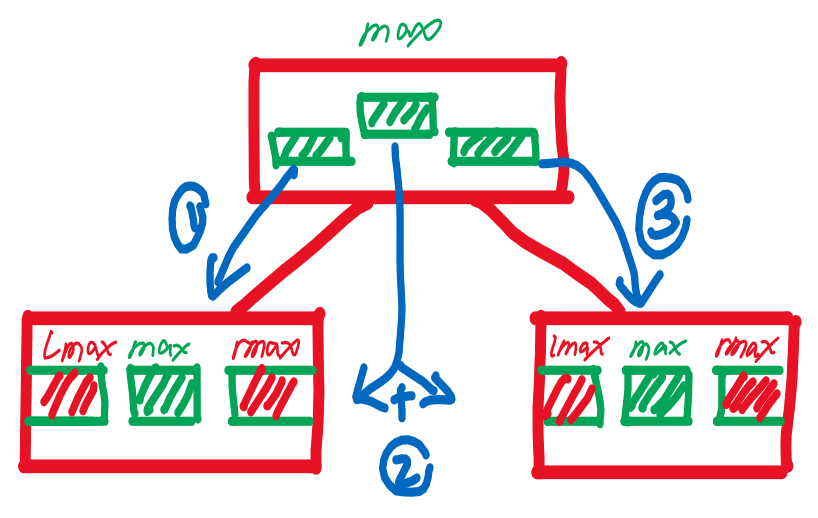
- ① 左子区间、② 左子区间+右子区间、③ 右子区间
-
- 【所以】需维护的值 [每个结点]
- 最大子段和,左侧最大子段和,右侧最大子段和,区间和值
- 为什么需要维护区间和值❓
- 思考和的维护
- 父结点所在区间的,有2种可能来源,取最大即可
- Ⅰ) 左子区间、Ⅱ) 左子区间+右子区间[有条件]
- ❗ 而第Ⅱ)种来源的成立条件是,左子区间的横跨整个子区间
- 判断此条件,不如直接维护区间和值[]
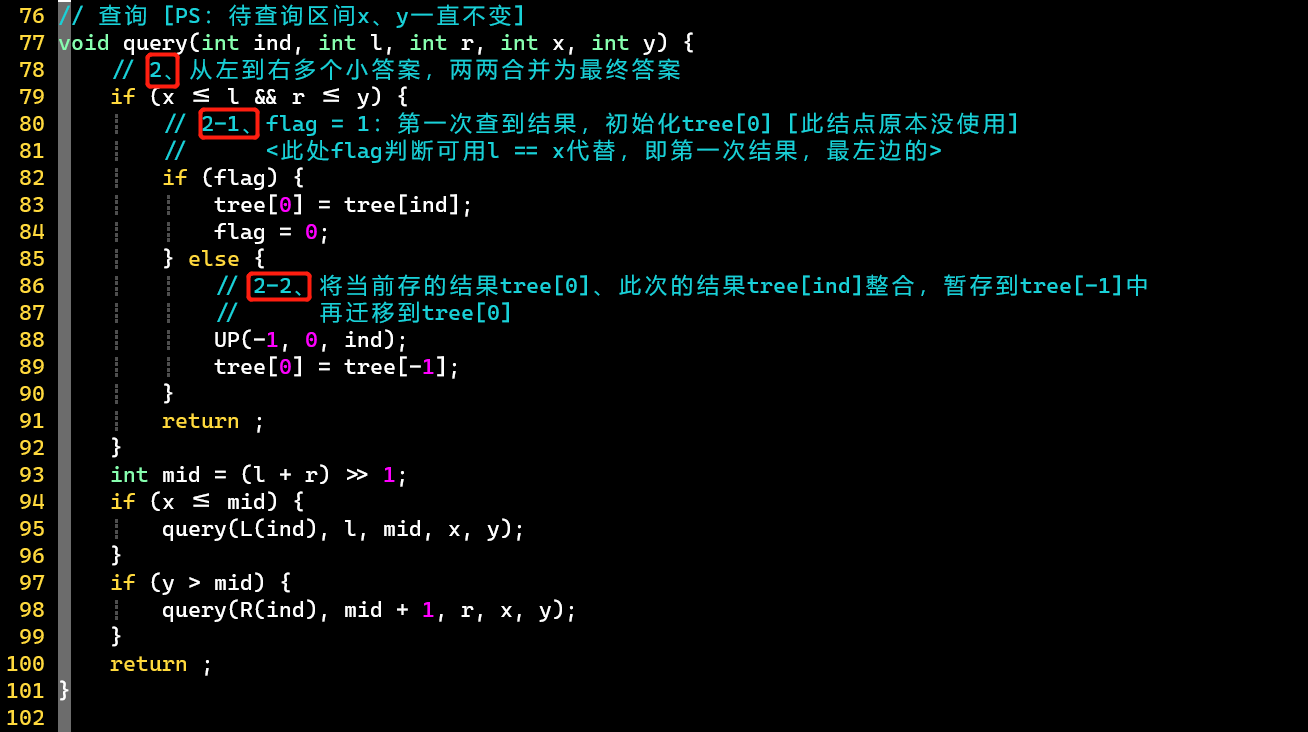
- 【注意】最终求答案时,是按顺序从左到右,一次两个的,合并结点
-
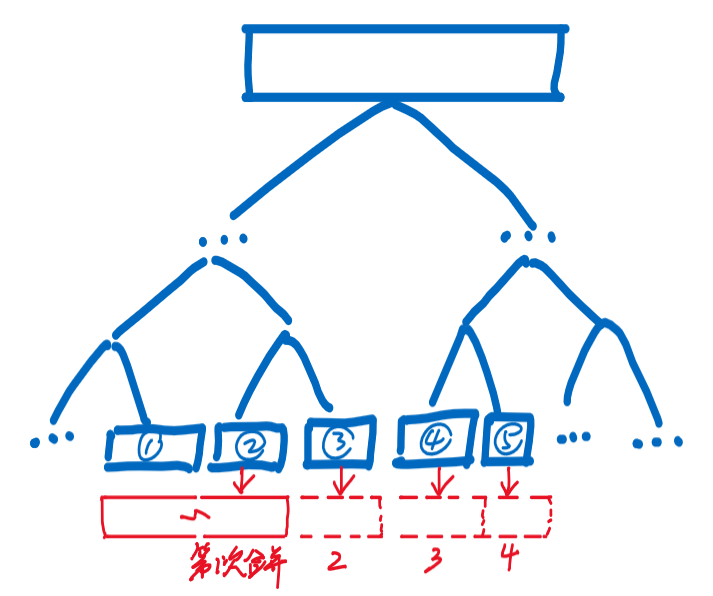
- 如:查询区间时
- 按照的顺序遍历结点
- 合并顺序依次为、、、,即每次合并2个结点为1个结点
- 最终合并为1个结点后,输出该结点对应的
- 具体见代码
-
- [PS] 线段树有点儿难度的题目
- 代码
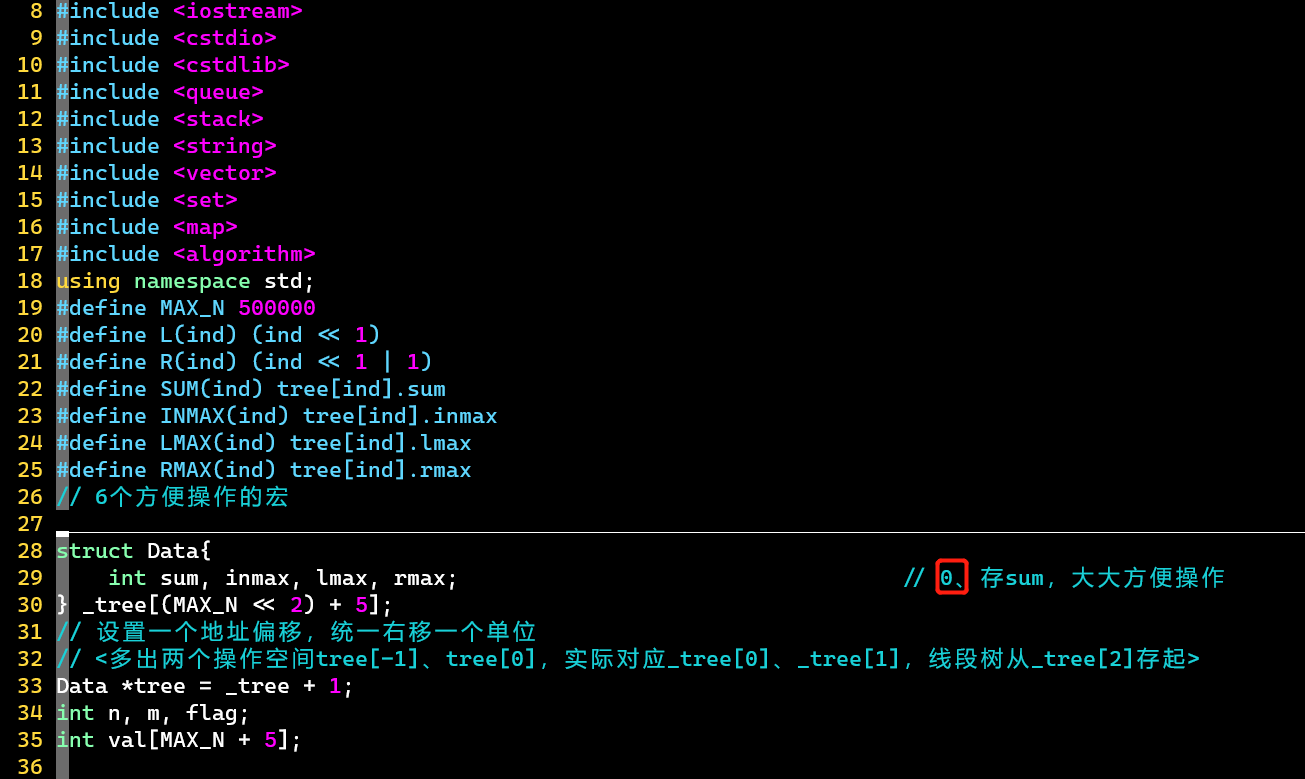
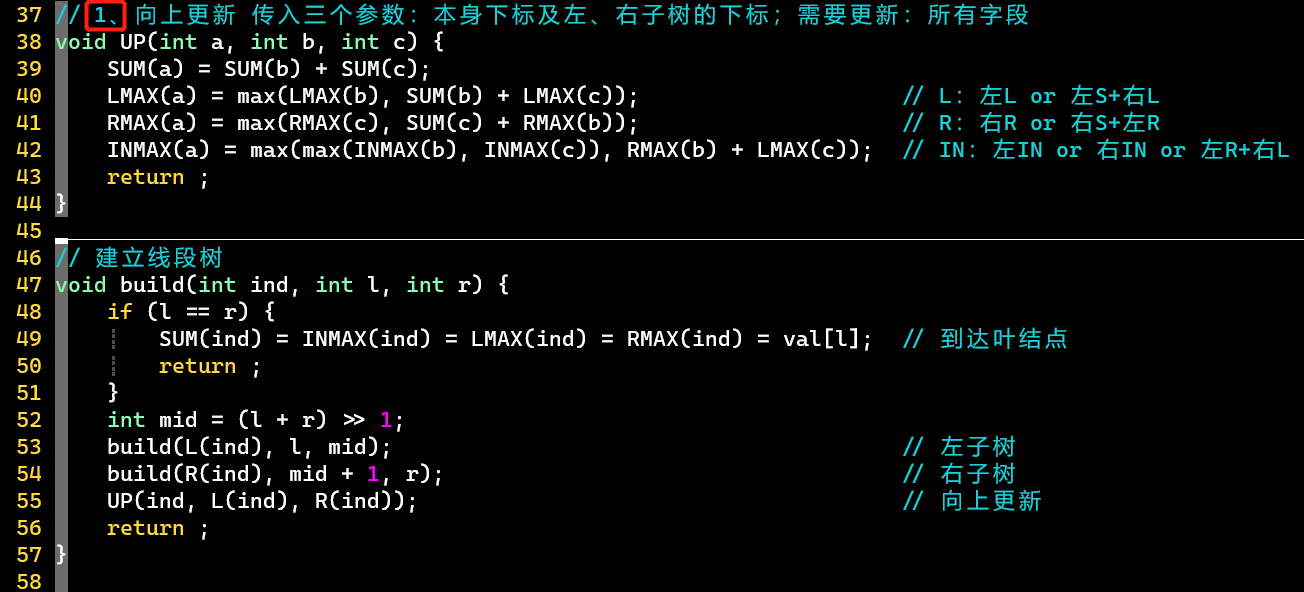
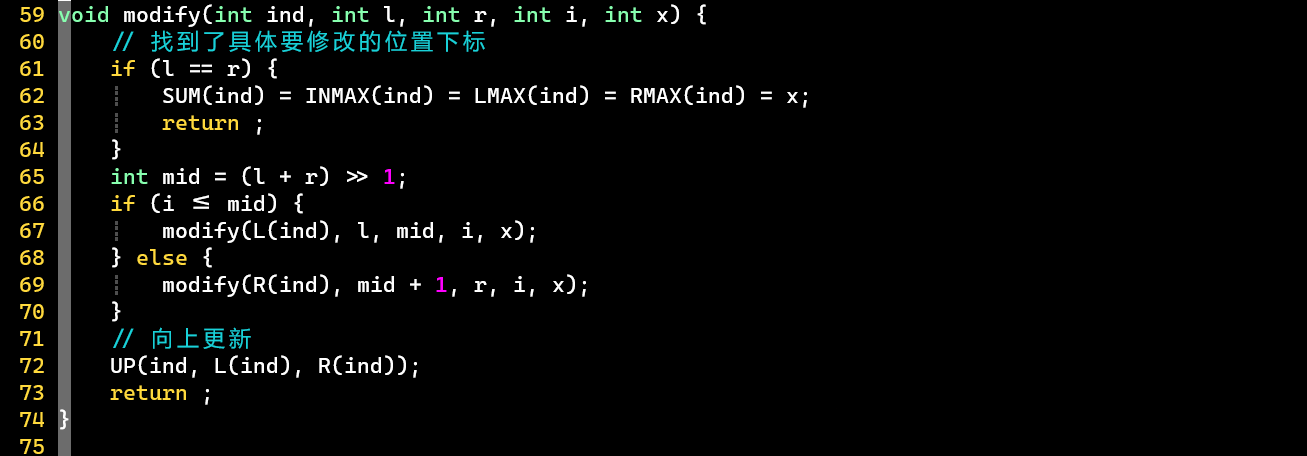
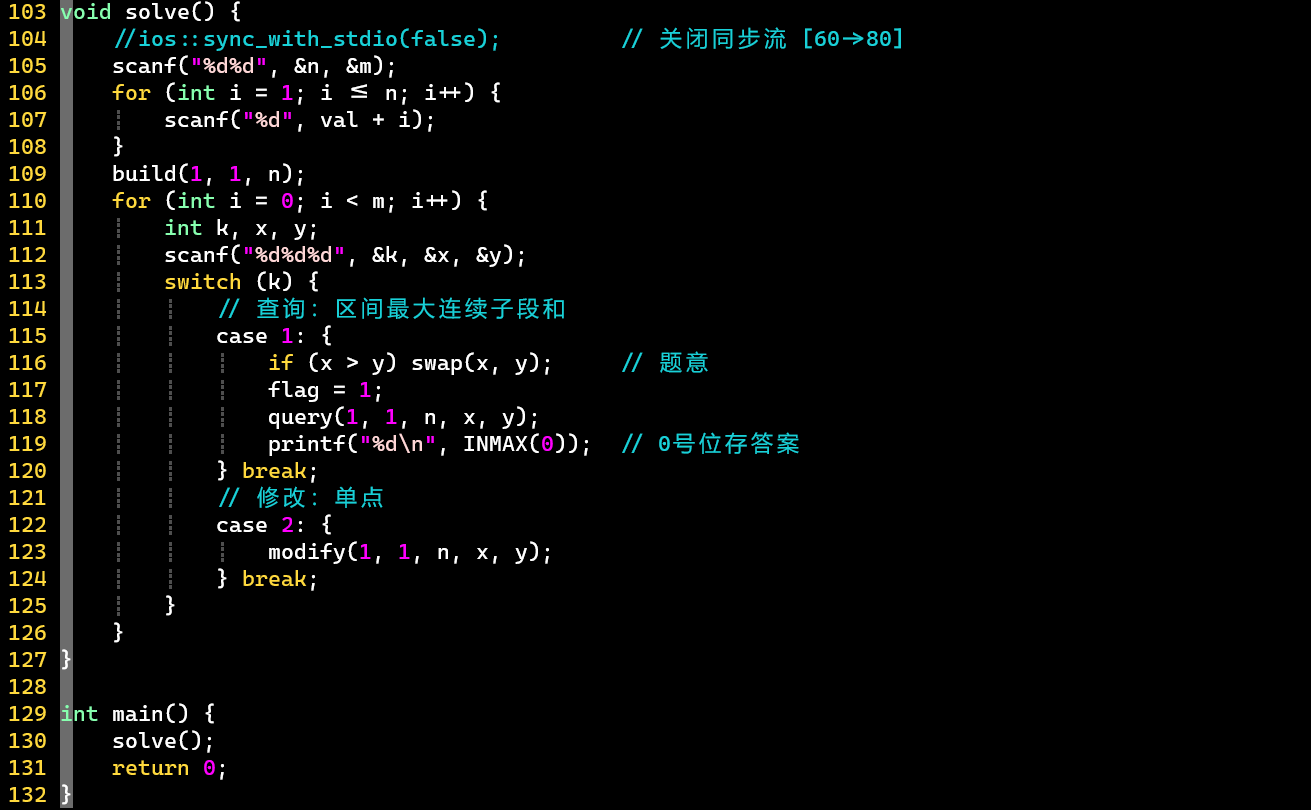
- ⭐关键点:标号的操作
- 0、sum的使用:减少条件判断
- 1、向上更新策略:传入3个参数,为了方便,也为了第88行的合并策略
- 2、查询的合并策略:每次合并1个结点,将合并的结点暂存到其它变量上,再转回来
- [PS]
- 不涉及区间修改,所以此线段数没有下沉标记 [懒标记] 操作
- 根据题意,需特殊处理的情况
Tips
- 树状数组一般用于解决前缀和问题
- 线段树应用更广泛,一般用于解决包含前缀和问题的区间操作问题
- 根据问题性质,寻找合适的算法与数据结构


